Middle Columbia River Fish Indexing Analysis 2019
The suggested citation for this analytic report is:
Thorley, J.L. and Amies-Galonski E. (2020) Middle Columbia River Fish Indexing Analysis 2019. A Poisson Consulting Analytic Appendix. URL: https://www.poissonconsulting.ca/f/1050384286.
Background
The key management questions to be addressed by the analyses are:
- Is there a change in abundance of adult life stages of fish using the Middle Columbia River (MCR) that corresponds with the implementation of a year-round minimum flow?
- Is there a change in growth rate of adult life stages of the most common fish species using the MCR that corresponds with the implementation of a year-round minimum flow?
- Is there a change in body condition (measured as a function of relative weight to length) of adult life stages of fish using the MCR that corresponds with the implementation of a year-round minimum flow?
- Is there a change in spatial distribution of adult life stages of fish using the MCR that corresponds with the implementation of a year-round minimum flow?
Other objectives include the estimation of species richness and diversity. The year-round minimum flow was implemented in the winter of 2010 at the same time that a fifth turbine was added.
Methods
Data Preparation
The data were collected by Okanagan Nation Alliance and Golder Associates.
Life-Stage
The four primary fish species were categorized as fry, juvenile or adult based on their lengths.
Statistical Analysis
Model parameters were estimated using Bayesian methods. The Bayesian estimates were produced using JAGS (Plummer 2015) and STAN (Carpenter et al. 2017). For additional information on Bayesian estimation the reader is referred to McElreath (2016).
Unless indicated otherwise, the Bayesian analyses used uninformative
normal prior distributions (Kery and Schaub 2011, 36). The posterior
distributions were estimated from 1500 Markov Chain Monte Carlo (MCMC)
samples thinned from the second halves of 3 chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that the split
\(\hat{R} \leq\) getOption("mb.rhat") (Kery and Schaub 2011, 40) and
\(\textrm{ESS} \geq 150\) for each of the monitored parameters
(Kery and Schaub 2011, 61). Where \(\hat{R}\) is the potential scale
reduction factor and \(\textrm{ESS}\) is the effective sample size.
The sensitivity of the estimates to the choice of priors was examined by multiplying the standard deviations of the normal (and log-normal) priors by 10 and using \(\hat{R}\) to test whether the samples where drawn from the same posterior distribution (Thorley and Andrusak 2017).
The parameters are summarised in terms of the point estimate, standard deviation (sd), the z-score, lower and upper 95% confidence/credible limits (CLs) and the p-value (Kery and Schaub 2011, 37, 42). For Bayesian models, the estimate is the median (50th percentile) of the MCMC samples, the z-score is \(\mathrm{mean}/\mathrm{sd}\) and the 95% CLs are the 2.5th and 97.5th percentiles. A p-value of 0.05 indicates that the lower or upper 95% CL is 0.
Where relevant, model adequacy was confirmed by examination of residual plots.
The results are displayed graphically by plotting the modeled relationships between particular variables and the response(s) with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values, respectively, while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). When informative the influence of particular variables is expressed in terms of the effect size (i.e., percent change in the response variable) with 95% confidence/credible intervals (CIs, Bradford, Korman, and Higgins 2005).
The analyses were implemented using R version 3.6.2
(R Core Team 2015) and the
mbr family of packages.
Growth
Annual growth was estimated from the inter-annual recaptures using the Fabens method (Fabens 1965) for estimating the von Bertalanffy (VB) growth curve (von Bertalanffy 1938). The VB curves is based on the premise that
\[ \frac{dl}{dt} = k (L_{\infty} - l)\]
where \(l\) is the length of the individual, \(k\) is the growth coefficient and \(L_{\infty}\) is the mean maximum length.
Integrating the above equation gives
\[ l_t = L_{\infty} (1 - e^{-k(t - t0)})\]
where \(l_t\) is the length at time \(t\) and \(t0\) is the time at which the individual would have had no length.
The Fabens form allows
\[ l_r = l_c + (L_{\infty} - l_c) (1 - e^{-kT})\]
where \(l_r\) is the length at recapture, \(l_c\) is the length at capture and \(T\) is the time at large.
Key assumptions of the growth model include:
- \(k\) can vary with discharge regime and randomly with year.
- The residual variation in growth is normally distributed.
Mountain Whitefish with a FL \(>\) 250 mm at release were excluded from the growth analysis as they appeared to be undergoing biphasic growth.
Condition
Condition was estimated via an analysis of mass-length relations (He et al. 2008).
More specifically the model was based on the allometric relationship
\[ W = \alpha L^{\beta}\]
where \(W\) is the weight (mass), \(\alpha\) is the coefficent, \(\beta\) is the exponent and \(L\) is the length.
To improve chain mixing the relation was log-transformed, i.e.,
\[ \log(W) = \log(\alpha) + \beta \log(L)\]
and the logged lengths centered, i.e., \(\log(L) - \text{mean}({\log(L)})\), prior to model fitting.
Key assumptions of the condition model include:
- \(\alpha\) can vary with the regime and season and randomly with year.
- \(\beta\) can vary with the regime and season and randomly with year.
- The residual variation in weight is log-normally distributed.
Fry were excluded from the condition analysis.
Occupancy
Occupancy, which is the probability that a particular species was present at a site, was estimated from the temporal replication of detection data (Kery and Schaub 2011, 414–18), i.e., each site was surveyed multiple times within a season. A species was considered to have been detected if one or more individuals of the species were caught or counted. It is important to note that the model estimates the probability that the species was present at a given (or typical) site in a given (or typical) year as opposed to the probability that the species was present in the entire study area. We focused on Northern Pikeminnow, Burbot, Lake Whitefish, Rainbow Trout, Redside Shiner and Sculpins because they were low enough density to not to be present at all sites at all times yet were encounted sufficiently often to provide information on spatial and temporal changes.
Key assumptions of the occupancy model include:
- Occupancy varies with season.
- Occupancy varies randomly with site and site within year.
- The effect of year on occupancy is autoregressive with a lag of one year and varies with discharge regime.
- Sites are closed, i.e., the species is present or absent at a site for all the sessions in a particular season of a year.
- Observed presence is described by a bernoulli distribution, given occupancy.
Count
The count data were analysed using an overdispersed Poisson model (Kery 2010, pp 168-170; Kery and Schaub 2011, pp 55-56) to provide estimates of the lineal river count density (count/km). The model estimates the expected count which is the product of the abundance and observer efficiency. In order to interpret the estimates as relative densities it is necessary to assume that changes in observer efficiency are negligible.
Key assumptions of the count model include:
- The count density (count/km) varies as an exponential growth model with the rate of change varying with discharge regime.
- The count density varies with season.
- The count density varies randomly with site, year and site within year.
- The counts are gamma-Poisson distributed.
In the case of suckers the count model replaced the first assumption with
- The count density varies with discharge regime.
Movement
The extent to which sites are closed, i.e., fish remain at the same site between sessions, was evaluated from a logistic ANCOVA (Kery 2010). The model estimated the probability that intra-annual recaptures were caught at the same site versus a different one.
Key assumptions of the site fidelity model include:
- Site fidelity varies with season, fish length and the interaction between season and fish length.
- Observed site fidelity is Bernoulli distributed.
Fry were excluded from the movement analysis.
Observer Length Correction
The annual bias (inaccuracy) and error (imprecision) in observer’s fish length estimates were quantified from the divergence of the length distribution of their observed fish from the length distribution of the measured fish. More specifically, the percent length correction that minimised the Jensen-Shannon divergence (Lin 1991) between the two distributions provided a measure of the inaccuracy while the minimum divergence (the Jensen-Shannon divergence was calculated with log to base 2 which means it lies between 0 and 1) provided a measure of the imprecision.
Abundance
The catch and geo-referenced count data were analysed using a capture-recapture-based overdispersed gamma-Poisson model to provide estimates of capture efficiency and absolute abundance. To maximize the number of recaptures the model grouped all the sites into a supersite for the purposes of estimating the number of marked fish but analysed the total captures at the site level.
Key assumptions of the full abundance model include:
- The density (fish/km) varies as an exponential growth model with the rate of change varying with discharge regime.
- The density varies with season.
- The density varies randomly with site, year and site within year.
- Efficiency (probability of capture) varies by season and method (capture versus count).
- Efficiency varies randomly by session within season within year.
- Marked and unmarked fish have the same probability of capture.
- There is no tag loss, migration (at the supersite level), mortality or misidentification of fish.
- The number of fish caught is gamma-Poisson distributed.
- The overdispersion varies by encounter type (count versus capture).
In the case of Adult Suckers the abundance model replaced the first assumption with
- The density varies with discharge regime.
Distribution
The site within year random effects from the count and abundance models were analysed using a linear mixed model to estimate the distribution.
Key assumptions of the linear mixed model include:
- The effect varies by river kilometer.
- The effect of river kilometer varies by discharge regime.
- The effect of river kilometer varies randomly by year.
- The effect is normally distributed.
The effects are the predicted site within year random effects after accounting for all other predictors including the site and year random effects. As such an increase in the distribution represents an increase in the relative density of fish closer to Revelstoke Dam. A positive distribution does not however necessarily indicate that the density of fish is higher closer to Revelstoke Dam.
Species Richness
The estimated probabilities of presence for the six species considered in the occupany analyses were summed to give the expected species richnesses by site and year.
Species Evenness
The site and year estimates of the lineal bank count densities from the count model for Rainbow Trout, Suckers, Burbot and Northern Pikeminnow were combined with the equivalent count estimates for Juvenile and Adult Bull Trout and Adult Mountain Whitefish from the abundance model to calculate the shannon index of evenness \((E)\). The index was calculated using the following formula where \(S\) is the number of species and \(p_i\) is the proportion of the total count belonging to the ith species.
\[ E = \frac{-\sum p_i \log(p_i)}{\log(S)}\]
Species Diversity
The site and year estimates of the lineal bank count densities from the count model for Rainbow Trout, Suckers, Burbot and Northern Pikeminnow were combined with the equivalent count estimates for Adult Bull Trout and Adult Mountain Whitefish from the abundance model to calculate species diversity profiles (Leinster and Cobbold 2012). Species diversity profiles can take similarities among species into account, allow for a range of weightings of rare versus common species (via the \(q\) sensitivity parameter), and estimate the effective number of species.
Like the species richness and evenness estimates, the species diversity profile estimates treated all species equally. The \(q\) sensitivity parameter, which measures the insensitivity to rare species, ranged from \(0\) (equivalent to richness) through \(1\) (equivalent to evenness) to \(2\) (equivalent to Simpson (1949)).
Model Templates
Growth
.model {
bKIntercept ~ dnorm(0, 5^-2)
bKRegime[1] <- 0
for(i in 2:nRegime) {
bKRegime[i] ~ dnorm(0, 5^-2)
}
sKAnnual ~ dnorm(0, 5^-2) T(0, )
for (i in 1:nAnnual) {
bKAnnual[i] ~ dnorm(0, sKAnnual^-2)
log(bK[i]) <- bKIntercept + bKRegime[step(i - Threshold) + 1] + bKAnnual[i]
}
bLinf ~ dnorm(600, 300^-2) T(100, 1000)
sGrowth ~ dnorm(0, 100^-2) T(0, )
for (i in 1:length(Growth)) {
eGrowth[i] <- (bLinf - LengthAtRelease[i]) * (1 - exp(-sum(bK[Annual[i]:(Annual[i] + Years[i] - 1)])))
Growth[i] ~ dnorm(eGrowth[i], sGrowth^-2)
}
tGrowth <- bKRegime[2]
..Block 1. The model description.
Condition
.model {
bWeightIntercept ~ dnorm(5, 5^-2)
bWeightSlope ~ dnorm(3, 5^-2)
bWeightRegimeIntercept[1] <- 0
bWeightRegimeSlope[1] <- 0
for(i in 2:nRegime) {
bWeightRegimeIntercept[i] ~ dnorm(0, 5^-2)
bWeightRegimeSlope[i] ~ dnorm(0, 5^-2)
}
bWeightSeasonIntercept[1] <- 0
bWeightSeasonSlope[1] <- 0
for(i in 2:nSeason) {
bWeightSeasonIntercept[i] ~ dnorm(0, 5^-2)
bWeightSeasonSlope[i] ~ dnorm(0, 5^-2)
}
sWeightYearIntercept ~ dnorm(0, 1^-2) T(0,)
sWeightYearSlope ~ dnorm(0, 1^-2) T(0,)
for(yr in 1:nYear) {
bWeightYearIntercept[yr] ~ dnorm(0, sWeightYearIntercept^-2)
bWeightYearSlope[yr] ~ dnorm(0, sWeightYearSlope^-2)
}
sWeight ~ dnorm(0, 1^-2) T(0,)
for(i in 1:length(Year)) {
eWeightIntercept[i] <- bWeightIntercept + bWeightRegimeIntercept[Regime[i]] + bWeightSeasonIntercept[Season[i]] + bWeightYearIntercept[Year[i]]
eWeightSlope[i] <- bWeightSlope + bWeightRegimeSlope[Regime[i]] + bWeightSeasonSlope[Season[i]] + bWeightYearSlope[Year[i]]
log(eWeight[i]) <- eWeightIntercept[i] + eWeightSlope[i] * LogLength[i]
Weight[i] ~ dlnorm(log(eWeight[i]) , sWeight^-2)
}
tCondition1 <- bWeightRegimeIntercept[2]
tCondition2 <- bWeightRegimeSlope[2]
..Block 2. The model description.
Occupancy
.model {
bRate ~ dnorm(0, 5^-2)
sRateYear ~ dnorm(0, 5^-2) T(0,)
for(i in 1:nYear) {
bRateYear[i] ~ dnorm(0, sRateYear^-2)
}
bRateRev5 ~ dnorm(0, 5^-2)
bOccupancyYear[1] ~ dnorm(0, 5^-2)
for (i in 2:nYear) {
eRateYear[i-1] <- bRate + bRateYear[i-1] + bRateRev5 * YearRev5[i-1]
bOccupancyYear[i] <- bOccupancyYear[i-1] + eRateYear[i-1]
}
bOccupancySpring ~ dnorm(0, 5^-2)
sOccupancySite ~ dnorm(0, 5^-2) T(0,)
sOccupancySiteYear ~ dnorm(0, 5^-2) T(0,)
for (i in 1:nSite) {
bOccupancySite[i] ~ dnorm(0, sOccupancySite^-2)
for (j in 1:nYear) {
bOccupancySiteYear[i,j] ~ dnorm(0, sOccupancySiteYear^-2)
}
}
for (i in 1:length(Observed)) {
logit(eObserved[i]) <- bOccupancyYear[Year[i]] + bOccupancySpring * Spring[i] + bOccupancySite[Site[i]] + bOccupancySiteYear[Site[i], Year[i]]
Observed[i] ~ dbern(eObserved[i])
}
..Block 3. The model description.
Count
.model {
bDensity ~ dnorm(0, 5^-2)
bRate ~ dnorm(0, 5^-2)
bRateRev5 ~ dnorm(0, 5^-2)
bTrendYear[1] <- bDensity
for(i in 2:nYear) {
bTrendYear[i] <- bTrendYear[i-1] + bRate + bRateRev5 * YearRev5[i-1]
}
bDensitySeason[1] <- 0
for (i in 2:nSeason) {
bDensitySeason[i] ~ dnorm(0, 5^-2)
}
sDensityYear ~ dnorm(0, 5^-2) T(0,)
for (i in 1:nYear) {
bDensityYear[i] ~ dnorm(0, sDensityYear^-2)
}
sDensitySite ~ dnorm(0, 5^-2) T(0,)
sDensitySiteYear ~ dnorm(0, 2^-2) T(0,)
for (i in 1:nSite) {
bDensitySite[i] ~ dnorm(0, sDensitySite^-2)
for (j in 1:nYear) {
bDensitySiteYear[i, j] ~ dnorm(0, sDensitySiteYear^-2)
}
}
sDispersion ~ dnorm(0, 5^-2) T(0,)
for (i in 1:length(Year)) {
log(eDensity[i]) <- bTrendYear[Year[i]] + bDensitySeason[Season[i]] + bDensityYear[Year[i]] + bDensitySite[Site[i]] + bDensitySiteYear[Site[i],Year[i]]
eCount[i] <- eDensity[i] * SiteLength[i] * ProportionSampled[i]
eDispersion[i] ~ dgamma(1 / sDispersion^2, 1 / sDispersion^2)
Count[i] ~ dpois(eCount[i] * eDispersion[i])
}
tCount <- bRateRev5
..Block 4. The model description.
Movement
.model {
bMoved ~ dnorm(0, 5^-2)
bLength ~ dnorm(0, 5^-2)
bMovedSpring ~ dnorm(0, 5^-5)
bLengthSpring ~ dnorm(0, 5^-5)
for (i in 1:length(Moved)) {
logit(eMoved[i]) <- bMoved + bMovedSpring * Spring[i] + (bLength + bLengthSpring * Spring[i]) * Length[i]
Moved[i] ~ dbern(eMoved[i])
}
..Block 5.
Abundance
.model {
bDensity ~ dnorm(0, 5^-2)
bRate ~ dnorm(0, 5^-2)
bRateRev5 ~ dnorm(0, 5^-2)
bTrendYear[1] <- bDensity
for(i in 2:nYear) {
bTrendYear[i] <- bTrendYear[i-1] + bRate + bRateRev5 * YearRev5[i-1]
}
bDensitySeason[1] <- 0
for (i in 2:nSeason) {
bDensitySeason[i] ~ dnorm(0, 5^-2)
}
sDensityYear ~ dnorm(0, 5^-2) T(0,)
for (i in 1:nYear) {
bDensityYear[i] ~ dnorm(0, sDensityYear^-2)
}
sDensitySite ~ dnorm(0, 5^-2) T(0,)
sDensitySiteYear ~ dnorm(0, 2^-2) T(0,)
for (i in 1:nSite) {
bDensitySite[i] ~ dnorm(0, sDensitySite^-2)
for (j in 1:nYear) {
bDensitySiteYear[i, j] ~ dnorm(0, sDensitySiteYear^-2)
}
}
bEfficiency ~ dnorm(0, 5^-2)
bEfficiencySeason[1] <- 0
for(i in 2:nSeason) {
bEfficiencySeason[i] ~ dnorm(0, 5^-2)
}
sEfficiencySessionSeasonYear ~ dnorm(0, 5^-2) T(0,)
for (i in 1:nSession) {
for (j in 1:nSeason) {
for (k in 1:nYear) {
bEfficiencySessionSeasonYear[i, j, k] ~ dnorm(0, sEfficiencySessionSeasonYear^-2)
}
}
}
bMultiplier <- 0
sDispersion ~ dnorm(0, 2^-2)
bMultiplierType[1] <- 0
sDispersionType[1] <- 0
for (i in 2:nType) {
bMultiplierType[i] ~ dnorm(0, 2^-2)
sDispersionType[i] ~ dnorm(0, 2^-2)
}
for(i in 1:length(EffIndex)) {
logit(eEff[i]) <- bEfficiency + bEfficiencySeason[Season[EffIndex[i]]] + bEfficiencySessionSeasonYear[Session[EffIndex[i]],Season[EffIndex[i]],Year[EffIndex[i]]]
Marked[EffIndex[i]] ~ dbin(eEff[i], Tagged[EffIndex[i]])
}
for (i in 1:length(Year)) {
logit(eEfficiency[i]) <- bEfficiency + bEfficiencySeason[Season[i]] + bEfficiencySessionSeasonYear[Session[i], Season[i], Year[i]]
log(eDensity[i]) <- bTrendYear[Year[i]] + bDensitySeason[Season[i]] + bDensityYear[Year[i]] + bDensitySite[Site[i]] + bDensitySiteYear[Site[i],Year[i]]
log(eMultiplier[i]) <- bMultiplier + bMultiplierType[Type[i]]
eCatch[i] <- eDensity[i] * SiteLength[i] * ProportionSampled[i] * eEfficiency[i] * eMultiplier[i]
log(esDispersion[i]) <- sDispersion + sDispersionType[Type[i]]
eDispersion[i] ~ dgamma(esDispersion[i]^-2 + 0.1, esDispersion[i]^-2 + 0.1)
Catch[i] ~ dpois(eCatch[i] * eDispersion[i])
}
tAbundance <- bRateRev5
..Block 6. The model description.
Distribution
.model {
bEffect ~ dnorm(0, 1^-2)
bRkm ~ dnorm(0, 1^-2)
bRkmRev5 ~ dnorm(0, 1^-2)
sRkmYear ~ dnorm(0, 1^-2) T(0,)
for(i in 1:nYear) {
bRkmYear[i] ~ dnorm(0, sRkmYear^-2)
}
sEffect ~ dnorm(0, 1^-2) T(0,)
for(i in 1:length(Effect)) {
eEffect[i] <- bEffect + (bRkm + bRkmRev5 * Rev5[i] + bRkmYear[Year[i]]) * Rkm[i]
Effect[i] ~ dnorm(eEffect[i], sEffect^-2)
}
tDistribution <- bRkmRev5Block 7. The model description.
Results
Tables
Stage
Table 1. Length cutoffs by species and stage.
| Species | Fry | Juvenile |
|---|---|---|
| Bull Trout | < 120 | < 400 |
| Mountain Whitefish | < 120 | < 175 |
| Rainbow Trout | < 120 | < 250 |
| Largescale Sucker | < 120 | < 350 |
Growth
Table 2. Parameter descriptions.
| Parameter | Description |
|---|---|
Annual[i] |
Year |
bK[i] |
Expected growth coefficient in the ith Annual |
bKAnnual[i] |
Effect of ith Annual on bKIntercept |
bKIntercept |
Intercept for log(bK) |
bKRegime[i] |
Effect of ith Regime on bKIntercept |
bLinf |
Mean maximum length |
eGrowth[i] |
Expected Growth of the ith fish |
Growth[i] |
Change in length of the ith fish between release
and recapture (mm) |
LengthAtRelease[i] |
Length of the ith fish when released (mm) |
sGrowth |
SD of residual variation about eGrowth |
sKAnnual |
SD of bKAnnual |
Threshold |
Last Annual of the first regime |
Years[i] |
Number of years between release and recapture for the
ith fish |
Bull Trout
Table 3. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -1.7507336 | 0.1199146 | -14.6232718 | -1.9888049 | -1.5167030 | 0.0006662 |
| bKRegime[2] | -0.0600006 | 0.1428115 | -0.4356453 | -0.3661568 | 0.2211612 | 0.6482345 |
| bLinf | 844.0686142 | 24.6485065 | 34.3096957 | 802.3650682 | 897.4461141 | 0.0006662 |
| sGrowth | 32.0269299 | 1.2930389 | 24.8580730 | 29.9001309 | 34.8539006 | 0.0006662 |
| sKAnnual | 0.2659911 | 0.0693731 | 3.9725837 | 0.1687522 | 0.4461194 | 0.0006662 |
| tGrowth | -0.0600006 | 0.1428115 | -0.4356453 | -0.3661568 | 0.2211612 | 0.6482345 |
Table 4. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 344 | 6 | 3 | 500 | 500 | 1128 | 1.002 | TRUE |
Table 5. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 344 | 6 | 3 | 500 | 1.002 | 1.004 | 1.002 | TRUE |
Mountain Whitefish
Table 6. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -1.7606502 | 0.1656696 | -10.621613 | -2.0833212 | -1.4416248 | 0.0006662 |
| bKRegime[2] | 0.0828494 | 0.2171573 | 0.394426 | -0.3511366 | 0.4929744 | 0.6495670 |
| bLinf | 287.1680765 | 2.3396592 | 122.772254 | 282.7681925 | 292.0508562 | 0.0006662 |
| sGrowth | 9.6000819 | 0.2015170 | 47.630110 | 9.2045096 | 9.9965840 | 0.0006662 |
| sKAnnual | 0.4095895 | 0.1020587 | 4.167034 | 0.2777268 | 0.6707852 | 0.0006662 |
| tGrowth | 0.0828494 | 0.2171573 | 0.394426 | -0.3511366 | 0.4929744 | 0.6495670 |
Table 7. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1142 | 6 | 3 | 500 | 500 | 1136 | 1.003 | TRUE |
Table 8. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 1142 | 6 | 3 | 500 | 1.003 | 1.013 | 1.006 | TRUE |
Largescale Sucker
Table 9. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -2.352517 | 3.470345 | -0.7511485 | -10.0123652 | 3.977219 | 0.4337109 |
| bKRegime[2] | -2.898824 | 3.450703 | -0.7691769 | -9.1704883 | 4.534619 | 0.4603598 |
| bLinf | 635.111272 | 99.015320 | 6.6794026 | 536.8266817 | 928.031775 | 0.0006662 |
| sGrowth | 8.981498 | 0.366308 | 24.5662641 | 8.3355939 | 9.754696 | 0.0006662 |
| sKAnnual | 2.116388 | 1.292681 | 1.8975718 | 0.9771194 | 6.022412 | 0.0006662 |
| tGrowth | -2.898824 | 3.450703 | -0.7691769 | -9.1704883 | 4.534619 | 0.4603598 |
Table 10. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 303 | 6 | 3 | 500 | 500 | 82 | 1.064 | FALSE |
Table 11. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 303 | 6 | 3 | 500 | 1.064 | 1.757 | 2.912 | FALSE |
Condition
Table 12. Parameter descriptions.
| Parameter | Description |
|---|---|
bWeightIntercept |
Intercept for eWeightIntercept |
bWeightRegimeIntercept[i] |
Effect of ith Regime on bWeightIntercept |
bWeightRegimeSlope[i] |
Effect of ith Regime on bWeightSlope |
bWeightSeasonIntercept[i] |
Effect of ith Season on bWeightIntercept |
bWeightSeasonSlope[i] |
Effect of ith Season on bWeightSlope |
bWeightSlope |
Intercept for eWeightSlope |
bWeightYearIntercept[i] |
Effect of ith Year on bWeightIntercept |
bWeightYearSlope[i] |
Random effect of ith Year on bWeightSlope |
eWeight[i] |
Expected Weight of the ith fish |
eWeightIntercept[i] |
Intercept for log(eWeight[i]) |
eWeightSlope[i] |
Effect of LogLength on eWeightIntercept |
LogLength[i] |
The centered log(Length) of the ith fish |
sWeight |
SD of residual variation about eWeight |
sWeightYearIntercept |
SD of bWeightYearIntercept |
sWeightYearSlope |
SD of bWeightYearSlope |
Weight[i] |
The Weight of the ith fish |
Bull Trout
Table 13. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 6.8166826 | 0.0242804 | 280.7480460 | 6.7704401 | 6.8659191 | 0.0006662 |
| bWeightRegimeIntercept[2] | -0.0838463 | 0.0336963 | -2.4701919 | -0.1495648 | -0.0182574 | 0.0139907 |
| bWeightRegimeSlope[2] | 0.0402081 | 0.0460121 | 0.8920033 | -0.0476286 | 0.1348475 | 0.3484344 |
| bWeightSeasonIntercept[2] | 0.0009707 | 0.0086753 | 0.0922100 | -0.0159284 | 0.0174969 | 0.9253831 |
| bWeightSeasonSlope[2] | 0.0085434 | 0.0220951 | 0.3811584 | -0.0356207 | 0.0515235 | 0.6828781 |
| bWeightSlope | 3.1675132 | 0.0331265 | 95.5808860 | 3.0986533 | 3.2312403 | 0.0006662 |
| sWeight | 0.1362534 | 0.0015990 | 85.1977311 | 0.1330747 | 0.1394445 | 0.0006662 |
| sWeightYearIntercept | 0.0675277 | 0.0140357 | 4.9424494 | 0.0483610 | 0.1030031 | 0.0006662 |
| sWeightYearSlope | 0.0867526 | 0.0211165 | 4.2331160 | 0.0562734 | 0.1389527 | 0.0006662 |
| tCondition1 | -0.0838463 | 0.0336963 | -2.4701919 | -0.1495648 | -0.0182574 | 0.0139907 |
| tCondition2 | 0.0402081 | 0.0460121 | 0.8920033 | -0.0476286 | 0.1348475 | 0.3484344 |
Table 14. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 3630 | 11 | 3 | 500 | 200 | 675 | 1.003 | TRUE |
Table 15. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 3630 | 11 | 3 | 500 | 1.003 | 1.003 | 1.002 | TRUE |
Mountain Whitefish
Table 16. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 4.8029945 | 0.0141002 | 340.6197156 | 4.7748676 | 4.8312753 | 0.0006662 |
| bWeightRegimeIntercept[2] | -0.0151951 | 0.0202780 | -0.7538523 | -0.0568943 | 0.0240782 | 0.4390406 |
| bWeightRegimeSlope[2] | -0.0061139 | 0.0247906 | -0.2576246 | -0.0552766 | 0.0416127 | 0.8121252 |
| bWeightSeasonIntercept[2] | -0.0446255 | 0.0038943 | -11.4842247 | -0.0525053 | -0.0371512 | 0.0006662 |
| bWeightSeasonSlope[2] | -0.1053670 | 0.0178666 | -5.8999711 | -0.1408853 | -0.0705854 | 0.0006662 |
| bWeightSlope | 3.2078663 | 0.0175648 | 182.6059766 | 3.1724569 | 3.2416189 | 0.0006662 |
| sWeight | 0.1001294 | 0.0007745 | 129.2741614 | 0.0985946 | 0.1016629 | 0.0006662 |
| sWeightYearIntercept | 0.0396337 | 0.0084986 | 4.8152238 | 0.0282522 | 0.0612275 | 0.0006662 |
| sWeightYearSlope | 0.0414961 | 0.0119166 | 3.5775354 | 0.0234636 | 0.0695947 | 0.0006662 |
| tCondition1 | -0.0151951 | 0.0202780 | -0.7538523 | -0.0568943 | 0.0240782 | 0.4390406 |
| tCondition2 | -0.0061139 | 0.0247906 | -0.2576246 | -0.0552766 | 0.0416127 | 0.8121252 |
Table 17. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 8530 | 11 | 3 | 500 | 500 | 1004 | 1.006 | TRUE |
Table 18. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 8530 | 11 | 3 | 500 | 1.006 | 1.006 | 1.15 | FALSE |
Rainbow Trout
Table 19. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 4.7264442 | 0.0178071 | 265.4560365 | 4.6920934 | 4.7632632 | 0.0006662 |
| bWeightRegimeIntercept[2] | -0.0150140 | 0.0249748 | -0.6173774 | -0.0650983 | 0.0335656 | 0.4856762 |
| bWeightRegimeSlope[2] | -0.0519394 | 0.0448721 | -1.1628595 | -0.1383590 | 0.0350962 | 0.2191872 |
| bWeightSeasonIntercept[2] | -0.0705237 | 0.0153196 | -4.6156100 | -0.1000832 | -0.0408214 | 0.0006662 |
| bWeightSeasonSlope[2] | 0.0222651 | 0.0364029 | 0.5943697 | -0.0485086 | 0.0933276 | 0.5536309 |
| bWeightSlope | 3.0875166 | 0.0332232 | 92.9310496 | 3.0201936 | 3.1579685 | 0.0006662 |
| sWeight | 0.1099768 | 0.0031358 | 35.1242239 | 0.1043694 | 0.1165475 | 0.0006662 |
| sWeightYearIntercept | 0.0398596 | 0.0120961 | 3.4381871 | 0.0232159 | 0.0696368 | 0.0006662 |
| sWeightYearSlope | 0.0667392 | 0.0223293 | 3.1109495 | 0.0353323 | 0.1193577 | 0.0006662 |
| tCondition1 | -0.0150140 | 0.0249748 | -0.6173774 | -0.0650983 | 0.0335656 | 0.4856762 |
| tCondition2 | -0.0519394 | 0.0448721 | -1.1628595 | -0.1383590 | 0.0350962 | 0.2191872 |
Table 20. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 663 | 11 | 3 | 500 | 500 | 1203 | 1.003 | TRUE |
Table 21. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 663 | 11 | 3 | 500 | 1.003 | 1.004 | 1.001 | TRUE |
Largescale Sucker
Table 22. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 6.8232546 | 0.0232227 | 293.810078 | 6.7778992 | 6.8667944 | 0.0006662 |
| bWeightSeasonIntercept[2] | 0.0216273 | 0.0053627 | 4.054425 | 0.0117158 | 0.0328505 | 0.0006662 |
| bWeightSeasonSlope[2] | 0.1629237 | 0.0465700 | 3.493556 | 0.0718370 | 0.2535204 | 0.0006662 |
| bWeightSlope | 2.9127933 | 0.0734495 | 39.626157 | 2.7561414 | 3.0586804 | 0.0006662 |
| sWeight | 0.0833673 | 0.0010978 | 75.946096 | 0.0812544 | 0.0856207 | 0.0006662 |
| sWeightYearIntercept | 0.0611456 | 0.0199913 | 3.262224 | 0.0390647 | 0.1148657 | 0.0006662 |
| sWeightYearSlope | 0.2076533 | 0.0674905 | 3.266476 | 0.1291200 | 0.3831665 | 0.0006662 |
Table 23. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 2769 | 7 | 3 | 500 | 500 | 843 | 1.002 | TRUE |
Table 24. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 2765 | 6 | 3 | 500 | 1.002 | 1.007 | 2.633 | FALSE |
Occupancy
Table 25. Parameter descriptions.
| Parameter | Description |
|---|---|
bOccupancySite[i] |
Effect of ith site on bOccupancyYear |
bOccupancySiteYear[i,j] |
Effect of ith site in jth year on bOccupancyYear |
bOccupancySpring |
Effect of spring on bOccupancyYear |
bOccupancyYear[i] |
Expected Occupancy in ith year |
bRate |
Intercept of eRateYear |
bRateRev5[i] |
Effect of Revelstoke 5 regime on bRate |
bRateYear[i] |
Effect of ith year on biRate |
eObserved[i] |
Probability of observing a species on ith site visit |
eRateYear[i] |
Change in bOccupancyYear between year i-1 and year i |
Observed[i] |
Whether the species was observed on ith site visit |
sOccupancySite |
SD of bOccupancySite |
sOccupancySiteYear |
SD of bOccupancySiteYear |
sRateYear |
SD of bRateYear |
Rainbow Trout
Table 26. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -0.0211189 | 0.2933838 | -0.0979971 | -0.5964877 | 0.5512443 | 0.9427049 |
| bRate | 0.2537841 | 0.3430187 | 0.6925871 | -0.5085145 | 0.8544788 | 0.4350433 |
| bRateRev5 | -0.2047145 | 0.5098728 | -0.4001313 | -1.2226440 | 0.8787705 | 0.6628914 |
| sOccupancySite | 2.0806027 | 0.4730078 | 4.5454854 | 1.4274104 | 3.3042769 | 0.0006662 |
| sOccupancySiteYear | 0.5931010 | 0.2000258 | 2.8809056 | 0.0950440 | 0.9331820 | 0.0006662 |
| sRateYear | 0.9728467 | 0.3069866 | 3.3034821 | 0.5344169 | 1.7067354 | 0.0006662 |
Table 27. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 366 | 1.005 | TRUE |
Burbot
Table 28. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -0.5055025 | 0.3039636 | -1.646470 | -1.0616464 | 0.0981813 | 0.1112592 |
| bRate | 0.4443332 | 0.3858177 | 1.195467 | -0.3066406 | 1.2791748 | 0.2005330 |
| bRateRev5 | -0.6188830 | 0.5591564 | -1.128256 | -1.7831547 | 0.4850129 | 0.2391739 |
| sOccupancySite | 1.0662578 | 0.3017792 | 3.686698 | 0.6769883 | 1.8392708 | 0.0006662 |
| sOccupancySiteYear | 0.4876430 | 0.2273156 | 2.091691 | 0.0259983 | 0.8943945 | 0.0006662 |
| sRateYear | 1.1010054 | 0.3185481 | 3.575430 | 0.6365314 | 1.8663881 | 0.0006662 |
Table 29. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 423 | 1.005 | TRUE |
Lake Whitefish
Table 30. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -4.8888136 | 0.7989035 | -6.2296245 | -6.7578043 | -3.6131507 | 0.0006662 |
| bRate | 0.2390948 | 0.4966443 | 0.4704596 | -0.7520939 | 1.1535805 | 0.6322452 |
| bRateRev5 | -0.3323371 | 0.7794873 | -0.4032121 | -1.8436480 | 1.2587995 | 0.6815456 |
| sOccupancySite | 0.5073103 | 0.1717557 | 3.1062233 | 0.2565075 | 0.9383171 | 0.0006662 |
| sOccupancySiteYear | 0.2061891 | 0.1606613 | 1.4294934 | 0.0075733 | 0.5900137 | 0.0006662 |
| sRateYear | 1.5804621 | 0.3645380 | 4.4716618 | 1.0709421 | 2.4733664 | 0.0006662 |
Table 31. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 194 | 1.024 | TRUE |
Northern Pikeminnow
Table 32. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -2.1552771 | 0.4337606 | -4.973836 | -3.0033473 | -1.3202058 | 0.0006662 |
| bRate | 0.3351248 | 0.2862747 | 1.212567 | -0.1742807 | 0.9804073 | 0.1832112 |
| bRateRev5 | -0.4626214 | 0.4161821 | -1.144838 | -1.3393860 | 0.3194777 | 0.2151899 |
| sOccupancySite | 1.3647952 | 0.3589283 | 3.945096 | 0.8552119 | 2.2392677 | 0.0006662 |
| sOccupancySiteYear | 0.5537642 | 0.2568455 | 2.104395 | 0.0483798 | 1.0224085 | 0.0006662 |
| sRateYear | 0.7056723 | 0.2677340 | 2.781286 | 0.3180342 | 1.3635894 | 0.0006662 |
Table 33. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 513 | 1.006 | TRUE |
Redside Shiner
Table 34. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -0.9379891 | 0.3706036 | -2.5505426 | -1.6802086 | -0.2304014 | 0.0099933 |
| bRate | 0.3703824 | 0.5136177 | 0.7603619 | -0.5354205 | 1.5738008 | 0.4230513 |
| bRateRev5 | -0.5140931 | 0.7206089 | -0.7622041 | -2.0820541 | 0.8429950 | 0.4083944 |
| sOccupancySite | 2.2327082 | 0.6040548 | 3.8822362 | 1.4683617 | 3.7530884 | 0.0006662 |
| sOccupancySiteYear | 0.2818792 | 0.2056617 | 1.5032140 | 0.0196938 | 0.7611805 | 0.0006662 |
| sRateYear | 1.3237075 | 0.4201057 | 3.3006207 | 0.7483029 | 2.3454497 | 0.0006662 |
Table 35. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 249 | 1.007 | TRUE |
Sculpins
Table 36. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySpring | -0.4346491 | 0.2748119 | -1.6123220 | -0.9821016 | 0.0799755 | 0.0992672 |
| bRate | 0.5347873 | 0.4357812 | 1.2439978 | -0.2644184 | 1.4457847 | 0.2138574 |
| bRateRev5 | -0.6518429 | 0.6551080 | -0.9900303 | -1.9479542 | 0.6253316 | 0.2898068 |
| sOccupancySite | 1.3207870 | 0.3031855 | 4.4996817 | 0.9151275 | 2.1170614 | 0.0006662 |
| sOccupancySiteYear | 0.4126556 | 0.2059560 | 1.9538603 | 0.0180123 | 0.7767846 | 0.0006662 |
| sRateYear | 1.2839029 | 0.3284961 | 4.0313897 | 0.8045447 | 2.0550941 | 0.0006662 |
Table 37. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 6 | 3 | 500 | 1000 | 224 | 1.008 | TRUE |
Count
Table 38. Parameter descriptions.
| Parameter | Description |
|---|---|
bDensity |
bTrendYear in the first year |
bDensitySeason |
Effect of season on bTrendYear |
bDensitySite[i] |
Effect of ith site on bTrendYear |
bDensitySiteYear[i,j] |
Effect of ith site in jth year on
bDensityTrend |
bDensityYear[i] |
Effect of ith year on bTrendYear |
bRate |
Exponential population growth rate |
bRateRev5 |
Effect of Rev5 on bRate |
bTrendYear[i] |
The intercept for the log(eDensity) in the ith
year |
Count[i] |
Count on ith site visit |
eCount[i] |
Expected count on ith site visit |
eDensity[i] |
Expected lineal count density on ith site visit |
eDispersion[i] |
Overdispersion on ith site visit |
ProportionSampled[i] |
Proportion of site sampled on ith site visit |
sDensitySite |
SD of bDensitySite |
sDensitySiteYear |
SD of bDensitySiteYear |
sDensityYear |
SD of bDensityYear |
sDispersion[i] |
SD of eDispersion |
SiteLength[i] |
Length of site on ith site visit |
YearRev5[i] |
Whether the rate of change between the ith and
i+1th year is effectd by Rev5 |
Rainbow Trout
Table 39. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | -2.7051949 | 0.6772050 | -4.036072 | -4.1463532 | -1.4863898 | 0.0006662 |
| bDensitySeason[2] | -0.1193521 | 0.1536112 | -0.736468 | -0.4120815 | 0.1798996 | 0.4710193 |
| bRate | 0.2416045 | 0.0711581 | 3.452179 | 0.1123462 | 0.3984610 | 0.0019987 |
| bRateRev5 | -0.3484113 | 0.1304420 | -2.696805 | -0.6201202 | -0.1138323 | 0.0099933 |
| sDensitySite | 1.5618622 | 0.3627564 | 4.435372 | 1.0473463 | 2.4749919 | 0.0006662 |
| sDensitySiteYear | 0.7064079 | 0.0775009 | 9.141961 | 0.5628694 | 0.8682872 | 0.0006662 |
| sDensityYear | 0.6272727 | 0.1787453 | 3.625837 | 0.3693837 | 1.0906850 | 0.0006662 |
| sDispersion | 0.7981945 | 0.0526826 | 15.192758 | 0.7014973 | 0.9106660 | 0.0006662 |
| tCount | -0.3484113 | 0.1304420 | -2.696805 | -0.6201202 | -0.1138323 | 0.0099933 |
Table 40. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 9 | 3 | 500 | 2000 | 980 | 1.006 | TRUE |
Burbot
Table 41. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | -2.9860636 | 0.7961686 | -3.765667 | -4.5799083 | -1.4077311 | 0.0006662 |
| bDensitySeason[2] | -0.7763300 | 0.2796950 | -2.789257 | -1.3585135 | -0.2739136 | 0.0046636 |
| bRate | 0.1790349 | 0.1107058 | 1.603171 | -0.0346883 | 0.3979308 | 0.0966023 |
| bRateRev5 | -0.4014537 | 0.2131198 | -1.882632 | -0.8440015 | 0.0286095 | 0.0606262 |
| sDensitySite | 0.8635717 | 0.2456301 | 3.687171 | 0.5418852 | 1.4862107 | 0.0006662 |
| sDensitySiteYear | 0.4372803 | 0.1828296 | 2.336221 | 0.0597502 | 0.7758318 | 0.0006662 |
| sDensityYear | 1.0901883 | 0.2991498 | 3.762872 | 0.6480600 | 1.8221336 | 0.0006662 |
| sDispersion | 1.2125365 | 0.1340482 | 9.033011 | 0.9569587 | 1.4710729 | 0.0006662 |
| tCount | -0.4014537 | 0.2131198 | -1.882632 | -0.8440015 | 0.0286095 | 0.0606262 |
Table 42. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 9 | 3 | 500 | 2000 | 1190 | 1.006 | TRUE |
Northern Pikeminnow
Table 43. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | -4.1309573 | 0.7767589 | -5.405655 | -5.8609401 | -2.7906326 | 0.0006662 |
| bDensitySeason[2] | -2.3853256 | 0.4331203 | -5.561123 | -3.2941309 | -1.6211892 | 0.0006662 |
| bRate | 0.3302540 | 0.0946643 | 3.565492 | 0.1626128 | 0.5379072 | 0.0006662 |
| bRateRev5 | -0.6243164 | 0.1678747 | -3.782043 | -0.9864425 | -0.3262295 | 0.0019987 |
| sDensitySite | 1.2642294 | 0.3432588 | 3.849017 | 0.8051259 | 2.1237908 | 0.0006662 |
| sDensitySiteYear | 0.6673665 | 0.1909880 | 3.411952 | 0.2062757 | 0.9854695 | 0.0006662 |
| sDensityYear | 0.6337221 | 0.2138734 | 3.105955 | 0.3330658 | 1.1557920 | 0.0006662 |
| sDispersion | 1.3366890 | 0.1301647 | 10.310899 | 1.1002730 | 1.6054051 | 0.0006662 |
| tCount | -0.6243164 | 0.1678747 | -3.782043 | -0.9864425 | -0.3262295 | 0.0019987 |
Table 44. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 9 | 3 | 500 | 2000 | 1070 | 1.007 | TRUE |
Suckers
Table 45. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 1.9723382 | 0.2166413 | 9.093113 | 1.5432369 | 2.4011244 | 0.0006662 |
| bDensityRev5 | 0.5783026 | 0.2597159 | 2.226959 | 0.0656159 | 1.0905701 | 0.0246502 |
| bDensitySeason[2] | -0.3095755 | 0.0928386 | -3.348808 | -0.4865168 | -0.1348317 | 0.0006662 |
| sDensitySite | 0.4500476 | 0.0989077 | 4.656642 | 0.3053964 | 0.6891601 | 0.0006662 |
| sDensitySiteYear | 0.5076887 | 0.0456408 | 11.125705 | 0.4214611 | 0.6024636 | 0.0006662 |
| sDensityYear | 0.5463992 | 0.0992974 | 5.587980 | 0.4008861 | 0.7852651 | 0.0006662 |
| sDispersion | 0.7383009 | 0.0221660 | 33.311984 | 0.6957616 | 0.7845337 | 0.0006662 |
| tCount | 0.5783026 | 0.2597159 | 2.226959 | 0.0656159 | 1.0905701 | 0.0246502 |
Table 46. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1096 | 8 | 3 | 500 | 200 | 142 | 1.038 | FALSE |
Movement
Table 47. Parameter descriptions.
| Parameter | Description |
|---|---|
bLength |
Effect of Length on bMoved |
bLengthSpring |
Effect of Spring on bLength |
bMoved |
Intercept for logit(eMoved) |
bMovedSpring |
Effect of Spring on bMoved |
eMoved[i] |
Probability of different site from previous encounter for
ith recaptured fish |
Length[i] |
Length of ith recaptured fish (mm) |
Moved[i] |
Indicates whether ith recaptured fish is recorded at a
different site from previous encounter |
Spring[i] |
Whether the ith recaptured is from the spring |
Bull Trout
Table 48. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | 0.0050559 | 0.0015796 | 3.2237394 | 0.0020402 | 0.0083934 | 0.0006662 |
| bLengthSpring | 0.0012484 | 0.0058311 | 0.3211759 | -0.0076176 | 0.0152995 | 0.8187875 |
| bMoved | -2.0021253 | 0.6898047 | -2.9212149 | -3.4733841 | -0.7255709 | 0.0019987 |
| bMovedSpring | 0.3117504 | 2.5278178 | 0.0604711 | -5.3193628 | 4.4640225 | 0.8907395 |
Table 49. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 157 | 4 | 3 | 500 | 500 | 1437 | 1.001 | TRUE |
Mountain Whitefish
Table 50. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | -0.0019543 | 0.0028975 | -0.6847212 | -0.0074879 | 0.0035420 | 0.4803464 |
| bLengthSpring | -0.0263823 | 0.0066429 | -3.9881570 | -0.0401646 | -0.0138978 | 0.0006662 |
| bMoved | 0.4406461 | 0.7379263 | 0.6124895 | -0.9888788 | 1.8485747 | 0.5416389 |
| bMovedSpring | 5.4182611 | 1.5846881 | 3.4179195 | 2.3832482 | 8.5514241 | 0.0006662 |
Table 51. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 489 | 4 | 3 | 500 | 500 | 1268 | 1 | TRUE |
Rainbow Trout
Table 52. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | 0.0114662 | 0.0059343 | 1.986689 | 0.0006735 | 0.0250390 | 0.0366422 |
| bLengthSpring | 0.2159914 | 0.1212505 | 1.869137 | 0.0275220 | 0.4828487 | 0.0126582 |
| bMoved | -3.5209461 | 1.6116435 | -2.280991 | -7.0724454 | -0.6771077 | 0.0139907 |
| bMovedSpring | -65.7943350 | 36.6070156 | -1.892888 | -147.2647827 | -9.1633549 | 0.0099933 |
Table 53. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 27 | 4 | 3 | 500 | 500 | 1167 | 1.002 | TRUE |
Largescale Sucker
Table 54. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | -0.0106151 | 0.0054874 | -1.979825 | -0.0224177 | -0.0006919 | 0.0379747 |
| bLengthSpring | -0.1762254 | 0.0847866 | -2.142366 | -0.3610148 | -0.0343018 | 0.0086609 |
| bMoved | 4.4296540 | 2.3704001 | 1.925367 | 0.1732403 | 9.4337950 | 0.0419720 |
| bMovedSpring | 77.3757147 | 37.3347441 | 2.135704 | 14.6155554 | 158.8981791 | 0.0086609 |
Table 55. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 81 | 4 | 3 | 500 | 500 | 427 | 1.008 | TRUE |
Abundance
Table 56. Parameter descriptions.
| Parameter | Description |
|---|---|
bDensity |
Intercept for log(eDensity) in the 1st year |
bDensitySeason[i] |
Effect of ith season on bTrendYear |
bDensitySite[i] |
Effect of ith site on bDensity |
bDensitySiteYear[i,j] |
Effect of ith site in jth year on
bDensity |
bDensityYear[i] |
Effect of ith year on bDensity |
bEfficiency |
Intercept for logit(eEfficiency) |
bEfficiencySeason[i] |
Effect of ith season on bEfficiency |
bEfficiencySessionSeasonYear[i, j, k] |
Effect of ith Session in jth Season
of kth Year on bEfficiency |
bRate |
Exponential annual population growth rate |
bRateRev5[i] |
Effect of Rev5 on bRate |
bTrendYear[i] |
Intercept for log(eDensity) in the ith
year |
Catch[i] |
Number of fish caught on ith site visit |
eAbundance[i] |
Predicted abundance on ith site visit |
eDensity[i] |
Predicted lineal density on ith site visit |
eEfficiency[i] |
Predicted efficiency during ith site visit |
Marked[i] |
Number of marked fish caught in ith river
visit |
sDensitySite |
SD of bDensitySite |
sDensitySiteYear |
SD of bDensitySiteYear |
sDensityYear |
SD of bDensityYear |
sEfficiencySessionSeasonYear |
SD of bEfficiencySessionSeasonYear |
Tagged[i] |
Number of fish tagged prior to ith river
visit |
Bull Trout
Juvenile
Table 57. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 2.0529633 | 0.3643553 | 5.6419537 | 1.2940096 | 2.7447415 | 0.0006662 |
| bDensitySeason[2] | 0.2339380 | 0.3533404 | 0.6687714 | -0.4216598 | 0.9338769 | 0.4990007 |
| bEfficiency | -3.1511169 | 0.1390130 | -22.6589741 | -3.4221171 | -2.8809197 | 0.0006662 |
| bEfficiencySeason[2] | -0.3669385 | 0.3539413 | -1.0534084 | -1.0944416 | 0.3094929 | 0.2818121 |
| bMultiplierType[2] | 0.4924246 | 0.1440083 | 3.4447712 | 0.2230068 | 0.7787287 | 0.0019987 |
| bRate | 0.1428264 | 0.0434402 | 3.2989324 | 0.0601781 | 0.2313121 | 0.0033311 |
| bRateRev5 | -0.1486458 | 0.0835254 | -1.7997614 | -0.3177113 | 0.0086817 | 0.0566289 |
| sDensitySite | 0.6293581 | 0.1521014 | 4.2631644 | 0.4161771 | 1.0120476 | 0.0006662 |
| sDensitySiteYear | 0.2826389 | 0.0532901 | 5.2830055 | 0.1718522 | 0.3807650 | 0.0006662 |
| sDensityYear | 0.4003514 | 0.1084853 | 3.7611028 | 0.2304797 | 0.6409416 | 0.0006662 |
| sDispersion | -0.8975232 | 0.1265749 | -7.1636252 | -1.1868920 | -0.6844391 | 0.0006662 |
| sDispersionType[2] | 0.4042719 | 0.2373376 | 1.6527969 | -0.1067815 | 0.8328237 | 0.1205863 |
| sEfficiencySessionSeasonYear | 0.2522319 | 0.0468564 | 5.3671331 | 0.1631056 | 0.3467806 | 0.0006662 |
| tAbundance | -0.1486458 | 0.0835254 | -1.7997614 | -0.3177113 | 0.0086817 | 0.0566289 |
Table 58. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1211 | 14 | 3 | 500 | 500 | 544 | 1.006 | TRUE |
Adult
Table 59. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 4.1859710 | 0.2580021 | 16.1719566 | 3.6486484 | 4.6571261 | 0.0006662 |
| bDensitySeason[2] | -0.2033853 | 0.3449450 | -0.5794384 | -0.8363666 | 0.5130081 | 0.5389740 |
| bEfficiency | -3.6192948 | 0.1184504 | -30.5606299 | -3.8540114 | -3.3957365 | 0.0006662 |
| bEfficiencySeason[2] | -0.0893283 | 0.3493405 | -0.2860700 | -0.8024300 | 0.5389374 | 0.7828115 |
| bMultiplierType[2] | 0.6087917 | 0.1190852 | 5.1062637 | 0.3835729 | 0.8434613 | 0.0006662 |
| bRate | 0.0182260 | 0.0256005 | 0.7258335 | -0.0352378 | 0.0703218 | 0.4523651 |
| bRateRev5 | -0.0050941 | 0.0500328 | -0.1205790 | -0.1048534 | 0.0929095 | 0.9280480 |
| sDensitySite | 0.5212359 | 0.1262549 | 4.3101459 | 0.3634835 | 0.8390878 | 0.0006662 |
| sDensitySiteYear | 0.4018795 | 0.0392624 | 10.2805731 | 0.3295881 | 0.4796723 | 0.0006662 |
| sDensityYear | 0.2002960 | 0.0824979 | 2.4730273 | 0.0379251 | 0.3794340 | 0.0006662 |
| sDispersion | -0.9085711 | 0.0861245 | -10.5559208 | -1.0893487 | -0.7475905 | 0.0006662 |
| sDispersionType[2] | 0.4059878 | 0.1669858 | 2.4245293 | 0.0692949 | 0.7318899 | 0.0179880 |
| sEfficiencySessionSeasonYear | 0.1999823 | 0.0414635 | 4.8791176 | 0.1242672 | 0.2851098 | 0.0006662 |
| tAbundance | -0.0050941 | 0.0500328 | -0.1205790 | -0.1048534 | 0.0929095 | 0.9280480 |
Table 60. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1211 | 14 | 3 | 500 | 500 | 585 | 1.008 | TRUE |
Mountain Whitefish
Juvenile
Table 61. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 5.6816464 | 0.6604471 | 8.6035822 | 4.3319739 | 7.0293233 | 0.0006662 |
| bDensitySeason[2] | 0.3877354 | 0.6940322 | 0.5775852 | -0.9862879 | 1.8043141 | 0.5483011 |
| bEfficiency | -5.7826757 | 0.4486936 | -12.9350860 | -6.8125697 | -4.9968378 | 0.0006662 |
| bEfficiencySeason[2] | 0.0998247 | 0.6950220 | 0.1240544 | -1.3376216 | 1.4191500 | 0.8840773 |
| bMultiplierType[2] | 0.8969023 | 0.1924674 | 4.6497038 | 0.5359927 | 1.2755229 | 0.0006662 |
| bRate | 0.0935275 | 0.1469269 | 0.6613852 | -0.1639698 | 0.4075821 | 0.5043304 |
| bRateRev5 | -0.1572920 | 0.1949248 | -0.8265433 | -0.5740876 | 0.1896977 | 0.4083944 |
| sDensitySite | 0.8950822 | 0.2138415 | 4.3546389 | 0.6112824 | 1.4368639 | 0.0006662 |
| sDensitySiteYear | 0.5395837 | 0.0618339 | 8.7534063 | 0.4259818 | 0.6700358 | 0.0006662 |
| sDensityYear | 0.4593405 | 0.1746362 | 2.7930515 | 0.2306607 | 0.8854366 | 0.0006662 |
| sDispersion | -0.5406260 | 0.0869359 | -6.2824077 | -0.7285570 | -0.3865931 | 0.0006662 |
| sDispersionType[2] | 0.6002065 | 0.1506491 | 4.0109040 | 0.3235035 | 0.9039499 | 0.0006662 |
| sEfficiencySessionSeasonYear | 0.3201542 | 0.0608110 | 5.2990462 | 0.2154955 | 0.4435075 | 0.0006662 |
| tAbundance | -0.1572920 | 0.1949248 | -0.8265433 | -0.5740876 | 0.1896977 | 0.4083944 |
Table 62. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 995 | 14 | 3 | 500 | 500 | 116 | 1.037 | FALSE |
Adult
Table 63. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 6.6330829 | 0.2123302 | 31.2507257 | 6.2198812 | 7.0452007 | 0.0006662 |
| bDensitySeason[2] | -0.6156399 | 0.1132639 | -5.4645941 | -0.8461007 | -0.4002648 | 0.0006662 |
| bEfficiency | -3.9832943 | 0.0592741 | -67.1998023 | -4.1011046 | -3.8668193 | 0.0006662 |
| bEfficiencySeason[2] | 0.8643610 | 0.1134215 | 7.5850353 | 0.6440628 | 1.0801909 | 0.0006662 |
| bMultiplierType[2] | 0.8309869 | 0.1170480 | 7.0989377 | 0.6029264 | 1.0579082 | 0.0006662 |
| bRate | -0.0033987 | 0.0180606 | -0.1833426 | -0.0378838 | 0.0331600 | 0.8574284 |
| bRateRev5 | 0.0245543 | 0.0346176 | 0.7059429 | -0.0464292 | 0.0904741 | 0.4963358 |
| sDensitySite | 0.5992936 | 0.1419010 | 4.3580822 | 0.4055336 | 0.9794851 | 0.0006662 |
| sDensitySiteYear | 0.4050866 | 0.0278353 | 14.5868181 | 0.3530109 | 0.4613234 | 0.0006662 |
| sDensityYear | 0.1187903 | 0.0625967 | 1.9073700 | 0.0099283 | 0.2524529 | 0.0006662 |
| sDispersion | -0.8099160 | 0.0364119 | -22.2428965 | -0.8809641 | -0.7406524 | 0.0006662 |
| sDispersionType[2] | 0.4337653 | 0.0943264 | 4.6141835 | 0.2467712 | 0.6173565 | 0.0006662 |
| sEfficiencySessionSeasonYear | 0.2215050 | 0.0281099 | 7.9075601 | 0.1715526 | 0.2807482 | 0.0006662 |
| tAbundance | 0.0245543 | 0.0346176 | 0.7059429 | -0.0464292 | 0.0904741 | 0.4963358 |
Table 64. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1211 | 14 | 3 | 500 | 500 | 196 | 1.017 | TRUE |
Rainbow Trout
Table 65. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 0.5035328 | 0.5535634 | 0.8991013 | -0.6415210 | 1.6055876 | 0.3550966 |
| bDensitySeason[2] | 0.1665738 | 0.6970374 | 0.3021429 | -1.0665170 | 1.6045870 | 0.8001332 |
| bEfficiency | -2.5466367 | 0.2585561 | -9.9087863 | -3.1236454 | -2.0773126 | 0.0006662 |
| bEfficiencySeason[2] | -0.4533962 | 0.6920429 | -0.6990281 | -1.8533202 | 0.8223461 | 0.4990007 |
| bMultiplierType[2] | -0.0299201 | 1.9889840 | 0.0117350 | -3.8220236 | 4.0732843 | 0.9906729 |
| bRate | 0.0023524 | 0.1369591 | -0.0186858 | -0.2877056 | 0.2683257 | 0.9853431 |
| bRateRev5 | 0.0825676 | 0.1830594 | 0.4605125 | -0.2820071 | 0.4425316 | 0.6215856 |
| sDensitySite | 1.1631629 | 0.3093726 | 3.9208599 | 0.7671309 | 1.9162633 | 0.0006662 |
| sDensitySiteYear | 0.5284092 | 0.1320284 | 3.9844240 | 0.2392489 | 0.7817148 | 0.0006662 |
| sDensityYear | 0.3544851 | 0.1994533 | 1.8540220 | 0.0270004 | 0.8289877 | 0.0006662 |
| sDispersion | -1.4727050 | 1.0531446 | -1.6568585 | -4.3706970 | -0.4486307 | 0.0006662 |
| sDispersionType[2] | -0.0967444 | 2.0336782 | -0.0198595 | -3.9784430 | 4.0945658 | 0.9653564 |
| sEfficiencySessionSeasonYear | 0.3314460 | 0.1346054 | 2.4330432 | 0.0448715 | 0.5855767 | 0.0006662 |
| tAbundance | 0.0825676 | 0.1830594 | 0.4605125 | -0.2820071 | 0.4425316 | 0.6215856 |
Table 66. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 875 | 14 | 3 | 500 | 500 | 132 | 1.016 | FALSE |
Largescale Sucker
Table 67. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 5.1056970 | 0.2403126 | 21.2628672 | 4.6068258 | 5.5729691 | 0.0006662 |
| bDensitySeason[2] | -0.0089223 | 0.5552050 | 0.0502835 | -0.9173956 | 1.2070935 | 0.9880080 |
| bEfficiency | -3.5133030 | 0.1438967 | -24.4181839 | -3.8002228 | -3.2455222 | 0.0006662 |
| bEfficiencySeason[2] | -1.1053125 | 0.5598503 | -2.0242550 | -2.3361830 | -0.1496616 | 0.0193205 |
| bMultiplierType[2] | 0.6392151 | 0.2209639 | 2.8979748 | 0.2108205 | 1.0853563 | 0.0059960 |
| sDensitySite | 0.4814094 | 0.1196857 | 4.1794057 | 0.3224456 | 0.7779551 | 0.0006662 |
| sDensitySiteYear | 0.4190435 | 0.0501355 | 8.3693694 | 0.3249745 | 0.5221869 | 0.0006662 |
| sDensityYear | 0.5051093 | 0.1780942 | 2.9973844 | 0.2689088 | 0.9405951 | 0.0006662 |
| sDispersion | -0.6902780 | 0.0677848 | -10.1966320 | -0.8308407 | -0.5620322 | 0.0006662 |
| sDispersionType[2] | 0.4027684 | 0.1289317 | 3.0948560 | 0.1457699 | 0.6401236 | 0.0033311 |
| sEfficiencySessionSeasonYear | 0.4853366 | 0.0702473 | 6.9731355 | 0.3678391 | 0.6408407 | 0.0006662 |
Table 68. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 780 | 11 | 3 | 500 | 500 | 436 | 1.006 | TRUE |
Distribution
Table 69. Parameter descriptions.
| Parameter | Description |
|---|---|
bEffect |
Intercept for eEffect |
bRkm |
Effect of Rkm on bEffect |
bRkmRev5 |
Effect of Rev5 on bRkm |
bRkmYear[i] |
Effect of ith year on bRkm |
eEffect |
Expected Effect |
Effect |
Estimated site and year effect from the count or abundance model |
Rkm |
Standardised river kilometre |
sEffect |
SD of residual variation in Effect |
sRkmYear |
SD of bRkmYear |
Bull Trout
Juvenile
Table 70. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | 0.0005560 | 0.0070110 | 0.0624877 | -0.0130753 | 0.0140627 | 0.9280480 |
| bRkm | -0.0024619 | 0.0037364 | -0.6466934 | -0.0093860 | 0.0050706 | 0.4963358 |
| bRkmRev5 | 0.0046702 | 0.0053132 | 0.8619732 | -0.0057774 | 0.0147606 | 0.3777482 |
| sEffect | 0.1175736 | 0.0050325 | 23.3820282 | 0.1083647 | 0.1278787 | 0.0006662 |
| sRkmYear | 0.0036914 | 0.0034803 | 1.2626905 | 0.0001472 | 0.0126233 | 0.0006662 |
| tDistribution | 0.0046702 | 0.0053132 | 0.8619732 | -0.0057774 | 0.0147606 | 0.3777482 |
Table 71. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 180 | 1.008 | TRUE |
Table 72. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.008 | 1.007 | 1.014 | TRUE |
Adult
Table 73. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | 0.0000161 | 0.0146368 | 0.0397544 | -0.0268423 | 0.0296271 | 0.9986676 |
| bRkm | -0.0068287 | 0.0091752 | -0.7582207 | -0.0251290 | 0.0114135 | 0.4203864 |
| bRkmRev5 | 0.0209920 | 0.0135455 | 1.5354268 | -0.0047073 | 0.0468544 | 0.1285809 |
| sEffect | 0.2532118 | 0.0112255 | 22.6257503 | 0.2333017 | 0.2753542 | 0.0006662 |
| sRkmYear | 0.0170700 | 0.0085107 | 2.0303378 | 0.0016103 | 0.0351675 | 0.0006662 |
| tDistribution | 0.0209920 | 0.0135455 | 1.5354268 | -0.0047073 | 0.0468544 | 0.1285809 |
Table 74. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 270 | 1.01 | TRUE |
Table 75. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.01 | 1.017 | 1.012 | TRUE |
Mountain Whitefish
Table 76. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | -0.0007872 | 0.0167896 | -0.0522631 | -0.0335893 | 0.0329969 | 0.9560293 |
| bRkm | -0.0063828 | 0.0148024 | -0.4466699 | -0.0356024 | 0.0228475 | 0.6335776 |
| bRkmRev5 | 0.0202507 | 0.0213924 | 0.9540819 | -0.0226802 | 0.0609906 | 0.3257828 |
| sEffect | 0.2873738 | 0.0129032 | 22.3162554 | 0.2647355 | 0.3141468 | 0.0006662 |
| sRkmYear | 0.0354937 | 0.0104231 | 3.5071894 | 0.0184673 | 0.0601103 | 0.0006662 |
| tDistribution | 0.0202507 | 0.0213924 | 0.9540819 | -0.0226802 | 0.0609906 | 0.3257828 |
Table 77. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 918 | 1.003 | TRUE |
Table 78. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.003 | 1.008 | 1.004 | TRUE |
Rainbow Trout
Table 79. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | 0.0014539 | 0.0205235 | 0.0629021 | -0.0381008 | 0.0423060 | 0.9626915 |
| bRkm | -0.0275127 | 0.0168693 | -1.6326304 | -0.0609019 | 0.0055611 | 0.1019320 |
| bRkmRev5 | 0.0506114 | 0.0251752 | 2.0188935 | 0.0034055 | 0.1011712 | 0.0353098 |
| sEffect | 0.3498825 | 0.0153002 | 22.9142667 | 0.3228388 | 0.3825013 | 0.0006662 |
| sRkmYear | 0.0401194 | 0.0127838 | 3.2422669 | 0.0195411 | 0.0692078 | 0.0006662 |
| tDistribution | 0.0506114 | 0.0251752 | 2.0188935 | 0.0034055 | 0.1011712 | 0.0353098 |
Table 80. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 956 | 1.004 | TRUE |
Table 81. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.004 | 1.003 | 1.002 | TRUE |
Burbot
Table 82. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | 0.0050579 | 0.0054731 | 0.9266906 | -0.0056143 | 0.0159120 | 0.3604264 |
| bRkm | -0.0001730 | 0.0038312 | -0.0712277 | -0.0077430 | 0.0074115 | 0.9653564 |
| bRkmRev5 | 0.0000940 | 0.0058511 | -0.0095035 | -0.0113190 | 0.0115683 | 0.9893404 |
| sEffect | 0.0926473 | 0.0039330 | 23.5786832 | 0.0852809 | 0.1005426 | 0.0006662 |
| sRkmYear | 0.0087613 | 0.0030949 | 2.9069827 | 0.0036781 | 0.0154934 | 0.0006662 |
| tDistribution | 0.0000940 | 0.0058511 | -0.0095035 | -0.0113190 | 0.0115683 | 0.9893404 |
Table 83. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 1007 | 1.004 | TRUE |
Table 84. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.004 | 1.004 | 1.002 | TRUE |
Northern Pikeminnow
Table 85. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | 0.0075408 | 0.0122483 | 0.5866496 | -0.0179544 | 0.0309517 | 0.5549634 |
| bRkm | -0.0060325 | 0.0070691 | -0.8410001 | -0.0201001 | 0.0074931 | 0.4057295 |
| bRkmRev5 | 0.0036046 | 0.0105771 | 0.3636478 | -0.0168000 | 0.0253749 | 0.7295137 |
| sEffect | 0.2073002 | 0.0090617 | 22.9017328 | 0.1904712 | 0.2255666 | 0.0006662 |
| sRkmYear | 0.0117230 | 0.0065332 | 1.8561004 | 0.0011888 | 0.0259696 | 0.0006662 |
| tDistribution | 0.0036046 | 0.0105771 | 0.3636478 | -0.0168000 | 0.0253749 | 0.7295137 |
Table 86. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 372 | 1.004 | TRUE |
Table 87. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.004 | 1.033 | 1.02 | TRUE |
Suckers
Table 88. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bEffect | -0.0033554 | 0.0193178 | -0.141963 | -0.0396495 | 0.0346014 | 0.8614257 |
| bRkm | -0.0176746 | 0.0159376 | -1.100899 | -0.0493184 | 0.0141814 | 0.2618254 |
| bRkmRev5 | 0.0248050 | 0.0232503 | 1.075789 | -0.0197124 | 0.0718914 | 0.2724850 |
| sEffect | 0.3216352 | 0.0142079 | 22.668846 | 0.2954979 | 0.3504725 | 0.0006662 |
| sRkmYear | 0.0388333 | 0.0117806 | 3.392725 | 0.0202747 | 0.0676331 | 0.0006662 |
| tDistribution | 0.0248050 | 0.0232503 | 1.075789 | -0.0197124 | 0.0718914 | 0.2724850 |
Table 89. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 10 | 1056 | 1.003 | TRUE |
Table 90. Sensitivity of posteriors to choice of priors.
| n | K | nchains | niters | rhat_1 | rhat_2 | rhat_all | converged |
|---|---|---|---|---|---|---|---|
| 285 | 6 | 3 | 500 | 1.003 | 1.004 | 1.003 | TRUE |
Effect Size
Table 91. The significance levels for the management hypotheses tested in the analyses. The Direction column indicates whether significant changes were positive or negative. The estimates and 95% lower and upper credible intervals are the effect sizes.
| Analysis | Species | Stage | Significance | Direction | Estimate | Lower | Upper |
|---|---|---|---|---|---|---|---|
| Abundance/Count - Density | Sucker | All | 0.0246502 | + | 78 % | 7 % | 198 % |
| Abundance/Count - Rate | Bull Trout | Juvenile | 0.0566289 | -14 % | -27 % | 1 % | |
| Abundance/Count - Rate | Bull Trout | Adult | 0.9280480 | -1 % | -10 % | 10 % | |
| Abundance/Count - Rate | Mountain Whitefish | Juvenile | 0.4083944 | -15 % | -44 % | 21 % | |
| Abundance/Count - Rate | Mountain Whitefish | Adult | 0.4963358 | 2 % | -5 % | 9 % | |
| Abundance/Count - Rate | Rainbow Trout | All | 0.0099933 | - | -29 % | -46 % | -11 % |
| Abundance/Count - Rate | Rainbow Trout | Adult | 0.6215856 | 9 % | -25 % | 56 % | |
| Abundance/Count - Rate | Burbot | All | 0.0606262 | -33 % | -57 % | 3 % | |
| Abundance/Count - Rate | Northern Pikeminnow | All | 0.0019987 | - | -46 % | -63 % | -28 % |
| Condition | Bull Trout | Juvenile | 0.0166556 | - | -9 % | -16 % | -3 % |
| Condition | Bull Trout | Adult | 0.0273151 | - | -7 % | -13 % | -1 % |
| Condition | Mountain Whitefish | Juvenile | 0.7441706 | -1 % | -7 % | 5 % | |
| Condition | Mountain Whitefish | Adult | 0.4177215 | -2 % | -6 % | 2 % | |
| Condition | Rainbow Trout | Juvenile | 0.8707528 | 0 % | -6 % | 7 % | |
| Condition | Rainbow Trout | Adult | 0.2485010 | -3 % | -9 % | 2 % | |
| Distribution | Bull Trout | Juvenile | 0.3777482 | 0 % | -1 % | 1 % | |
| Distribution | Bull Trout | Adult | 0.1285809 | 2 % | 0 % | 5 % | |
| Distribution | Mountain Whitefish | Adult | 0.3257828 | 2 % | -2 % | 6 % | |
| Distribution | Rainbow Trout | All | 0.0353098 | + | 5 % | 0 % | 11 % |
| Distribution | Sucker | All | 0.2724850 | 3 % | -2 % | 7 % | |
| Distribution | Burbot | All | 0.9893404 | 0 % | -1 % | 1 % | |
| Distribution | Northern Pikeminnow | All | 0.7295137 | 0 % | -2 % | 3 % | |
| Growth | Bull Trout | All | 0.6548967 | -7 % | -31 % | 24 % | |
| Growth | Mountain Whitefish | All | 0.7268488 | 8 % | -30 % | 64 % |
Figures
Growth
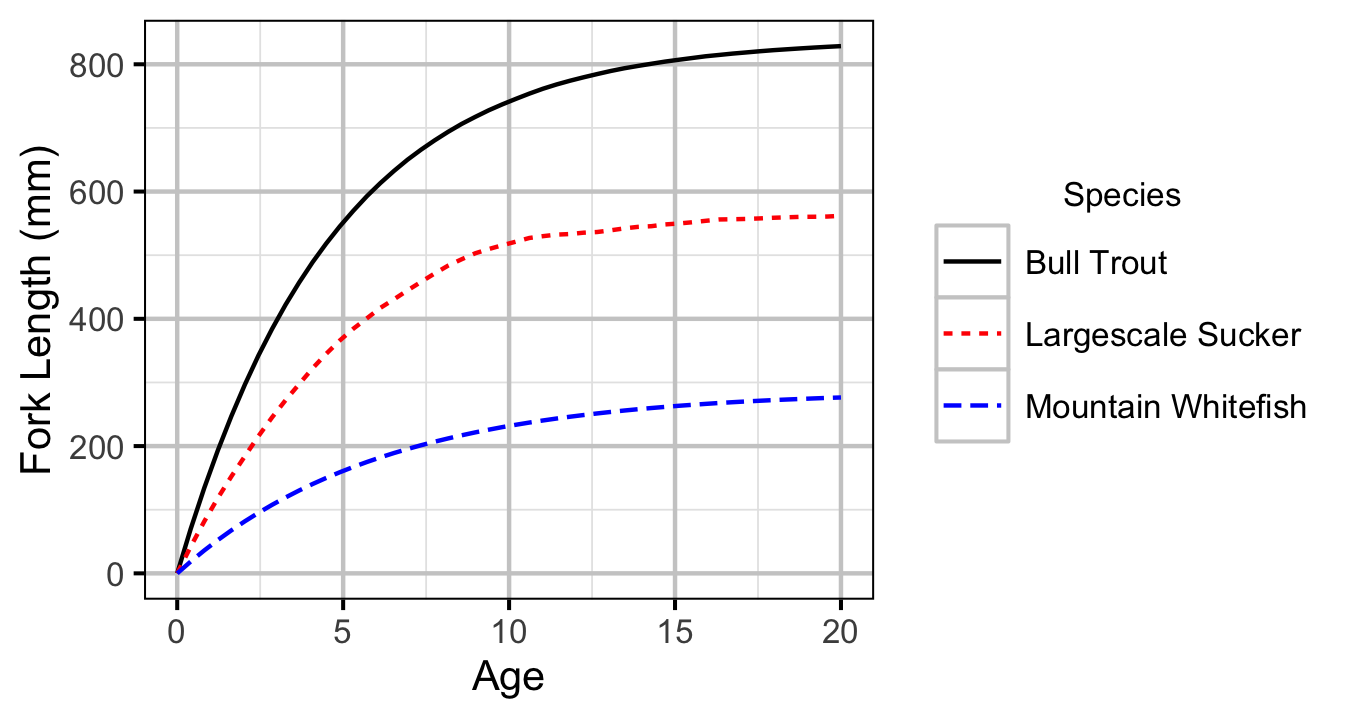
Figure 1. Predicted growth curve by species.
Bull Trout
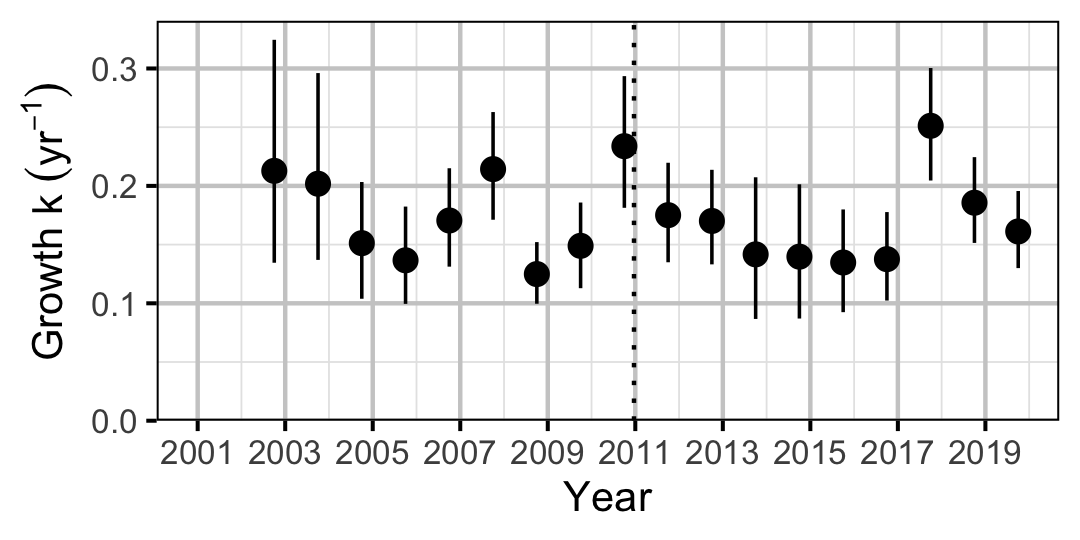
Figure 2. Predicted von Bertalanffy growth coefficient, k, by year (with 95% CIs).
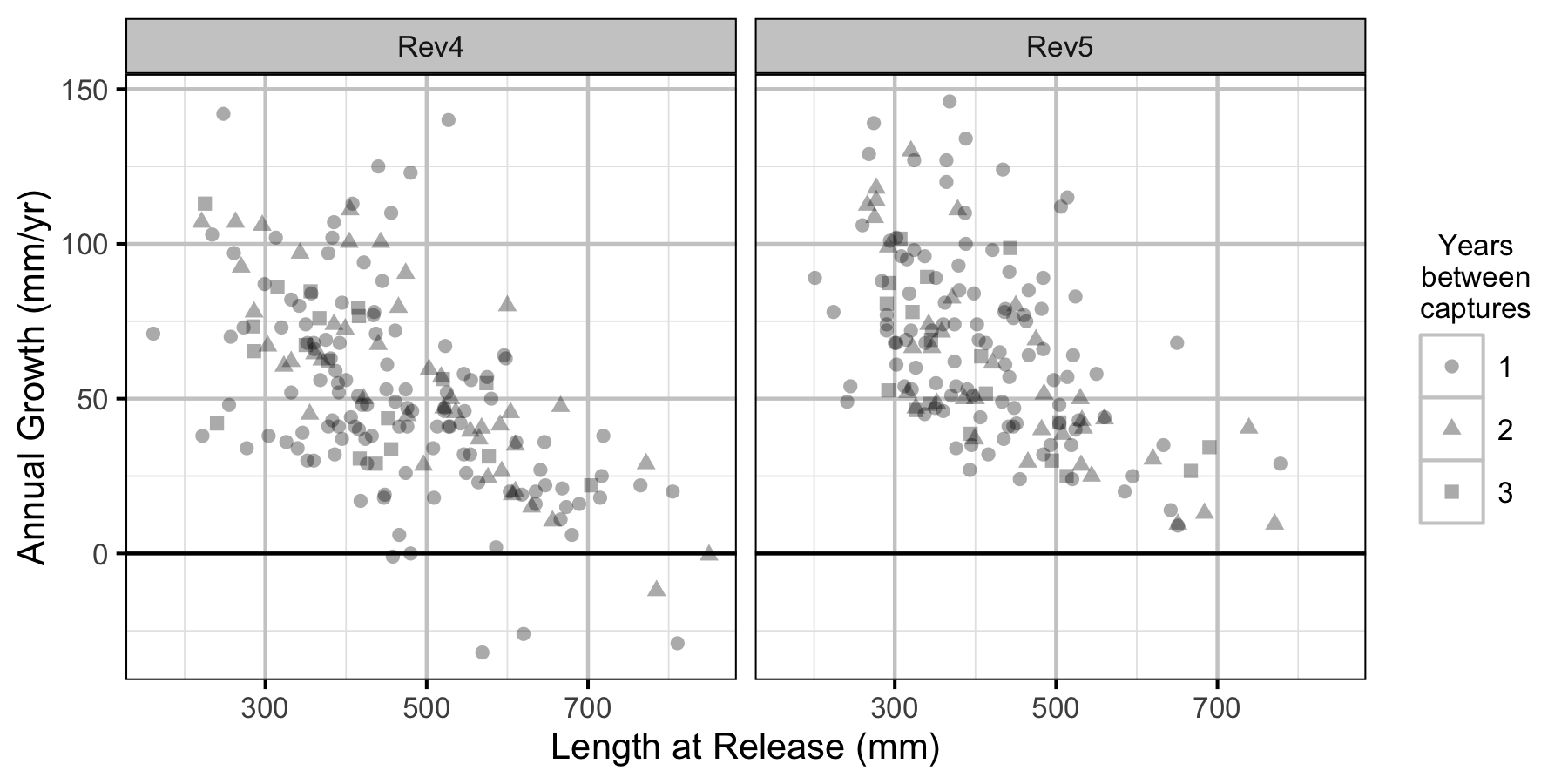
Figure 3. The mean annual fall to fall length change by length at release, flow regime and years at large.
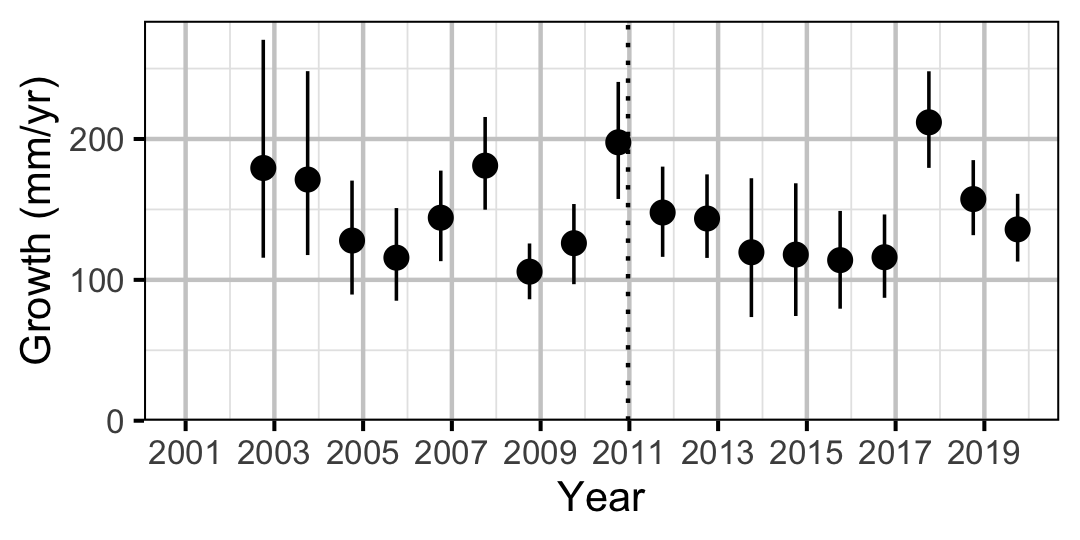
Figure 4. Predicted maximum growth by year (with 95% CIs).
Mountain Whitefish
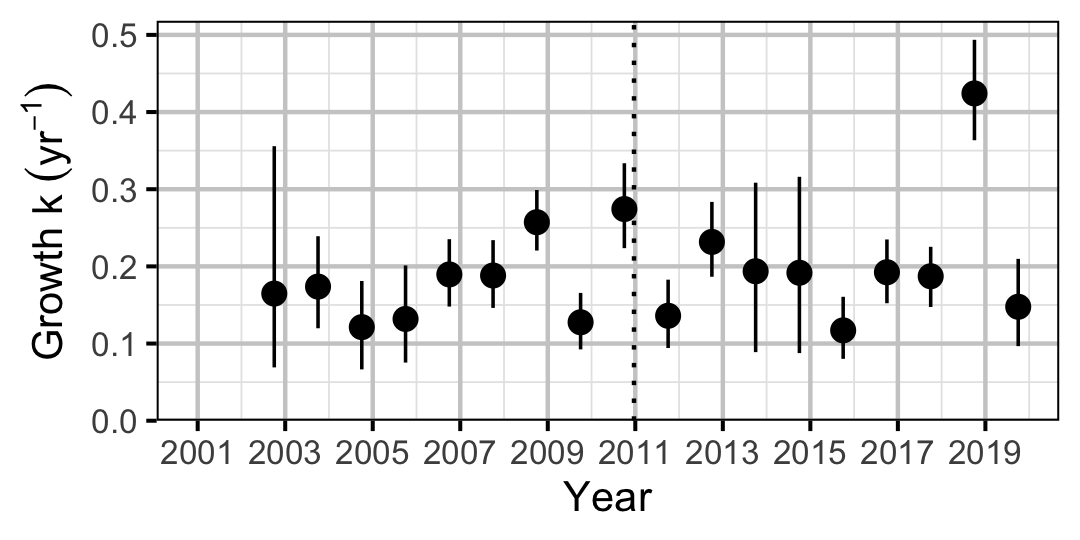
Figure 5. Predicted von Bertalanffy growth coefficient, k, by year (with 95% CIs).
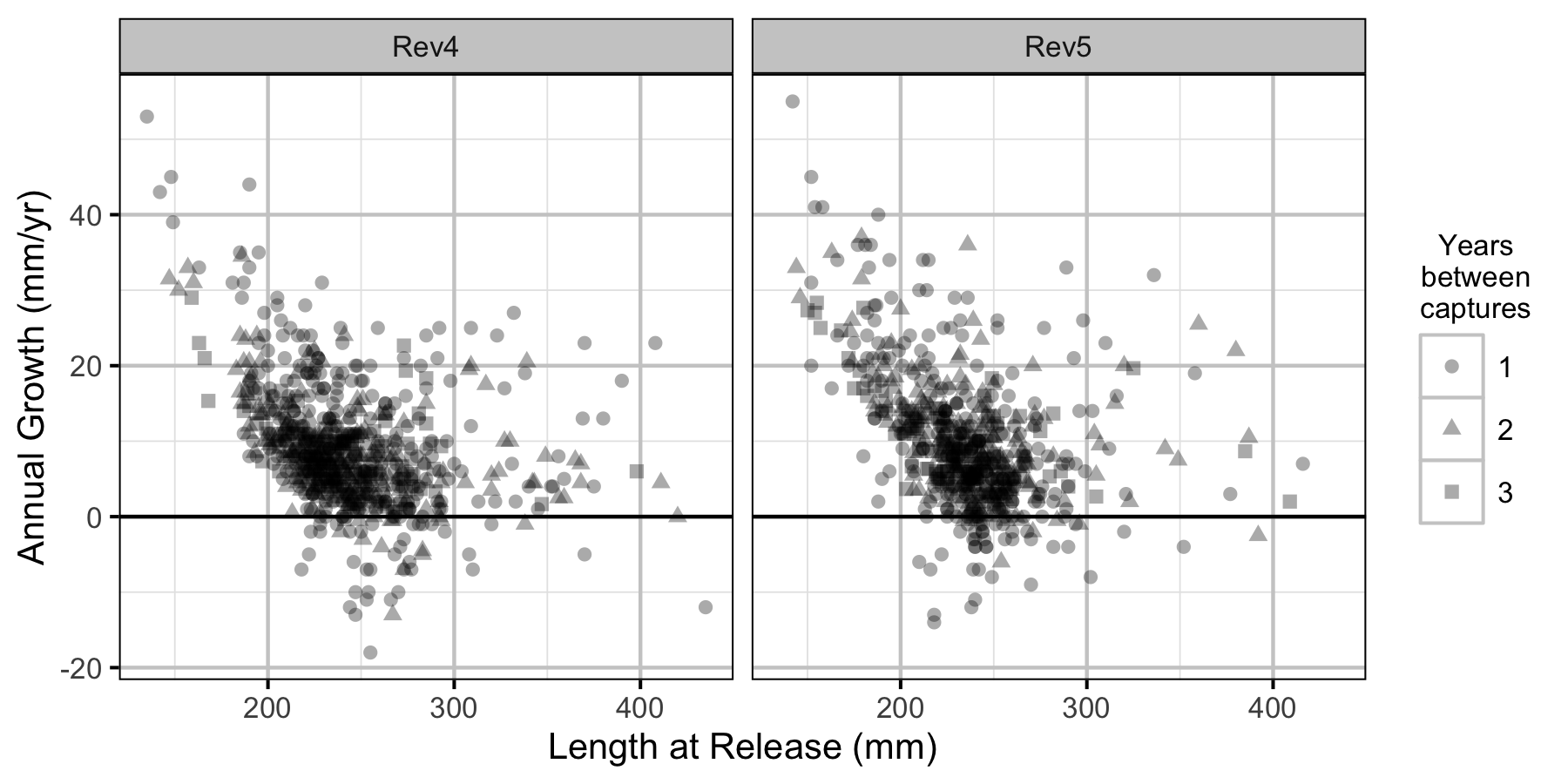
Figure 6. The mean annual fall to fall length change by length at release, flow regime and years at large.
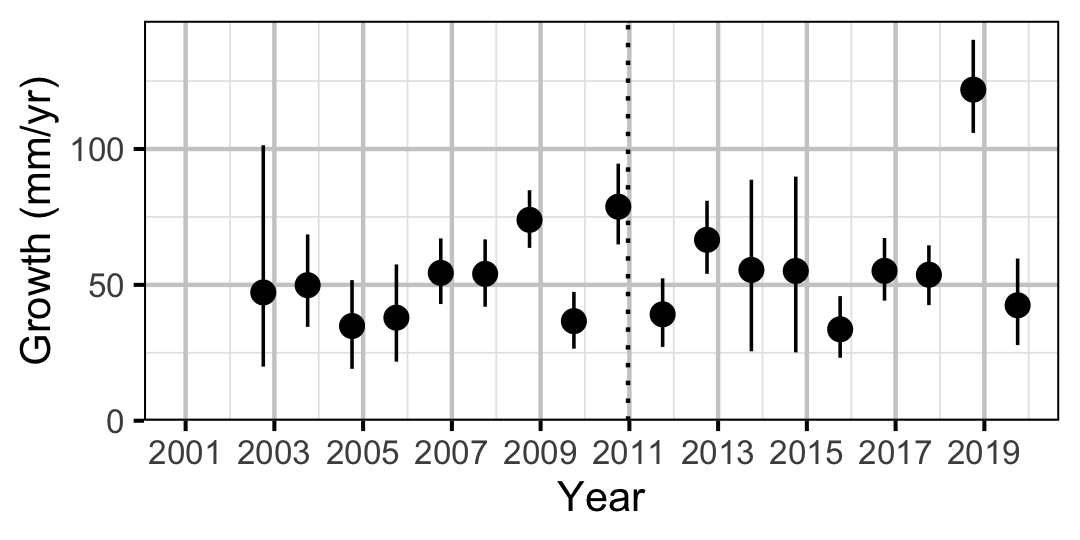
Figure 7. Predicted maximum growth by year (with 95% CIs).
Rainbow Trout
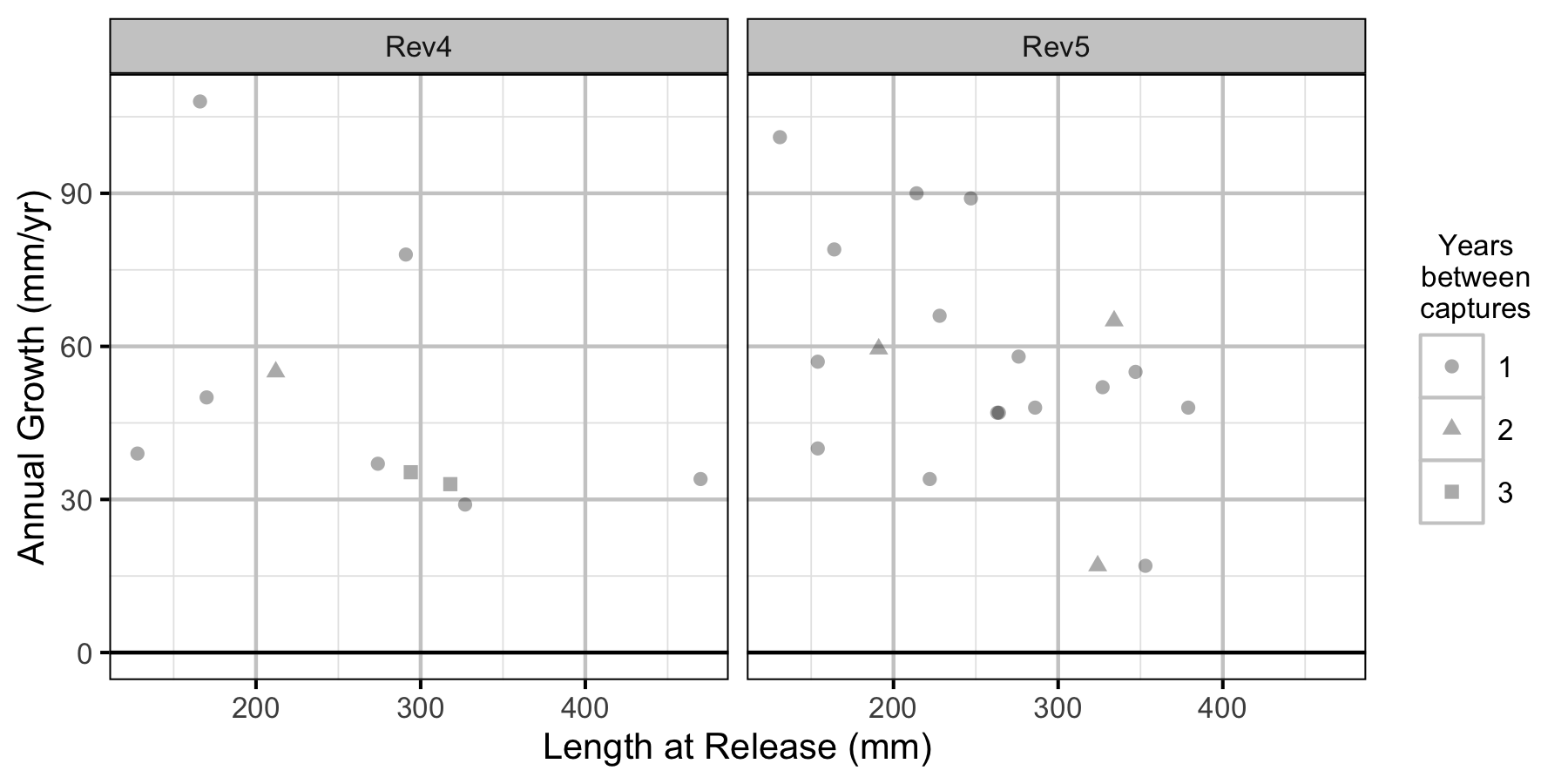
Figure 8. The mean annual fall to fall length change by length at release, flow regime and years at large.
Largescale Sucker
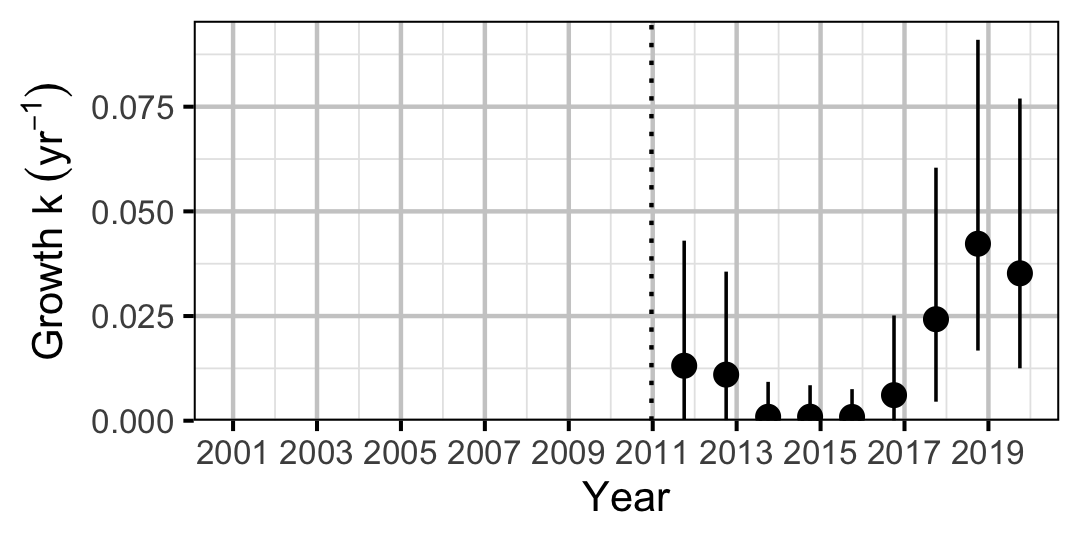
Figure 9. Predicted von Bertalanffy growth coefficient, k, by year (with 95% CIs).
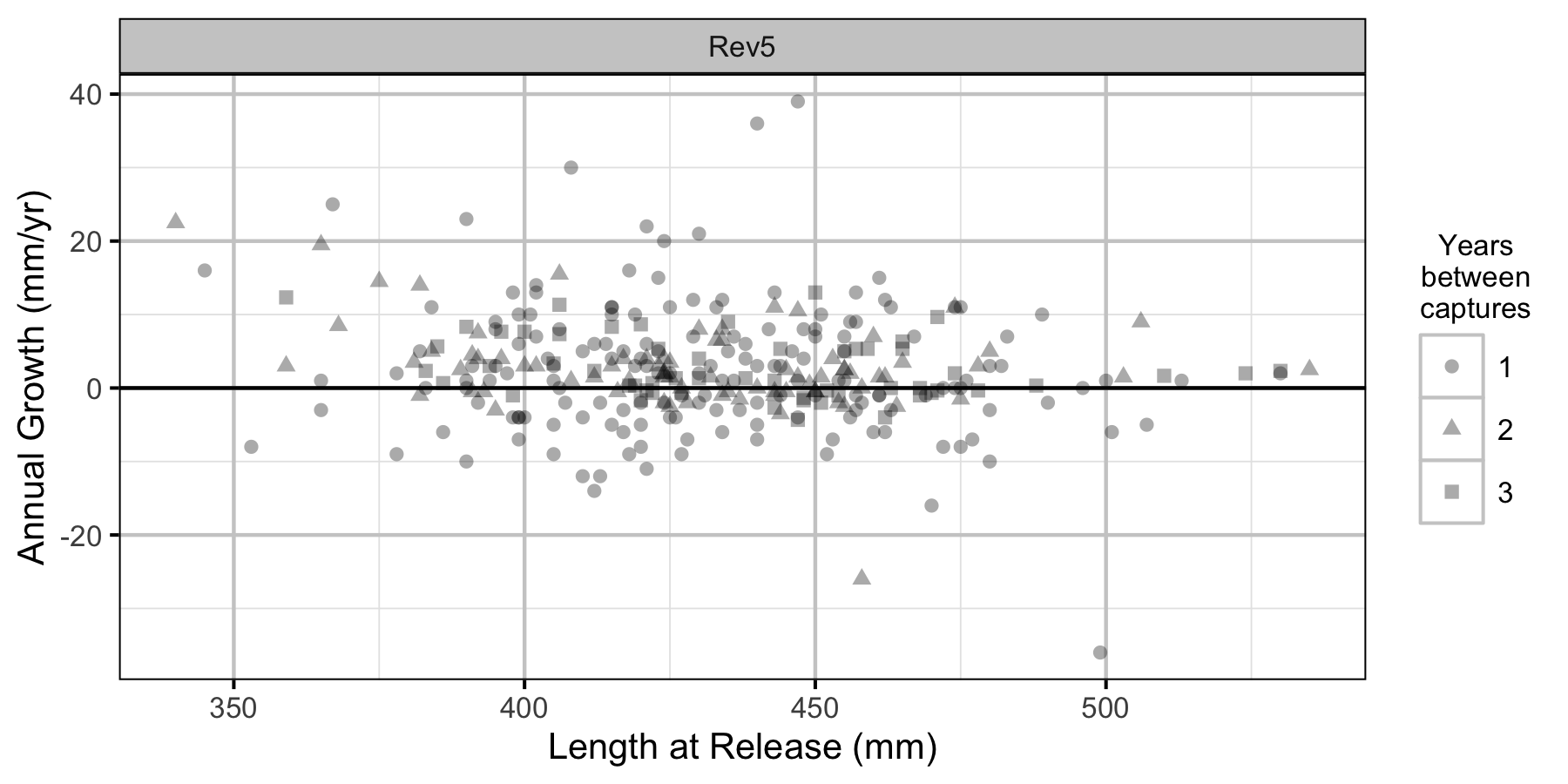
Figure 10. The mean annual fall to fall length change by length at release, flow regime and years at large.
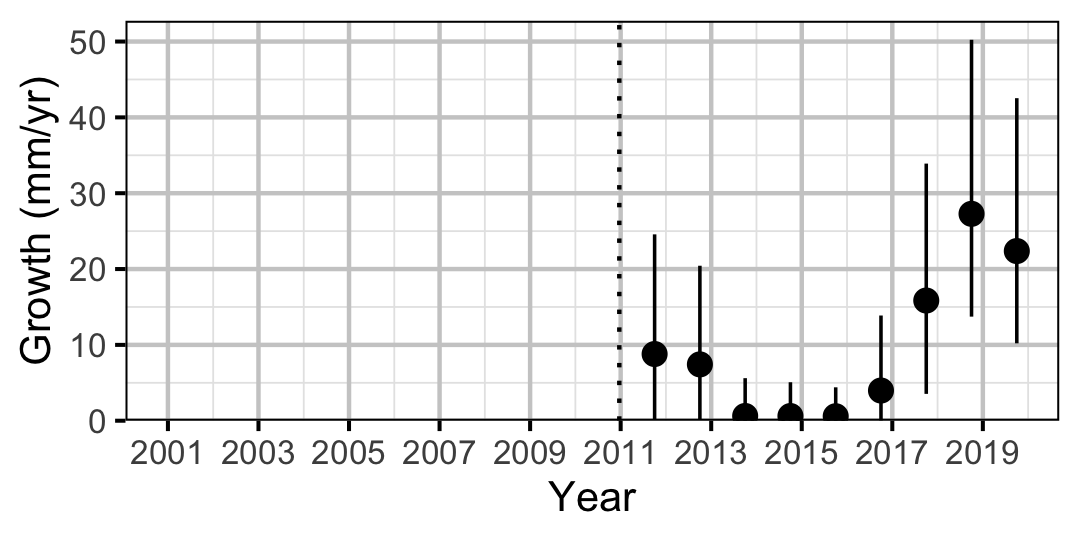
Figure 11. Predicted maximum growth by year (with 95% CIs).
Condition
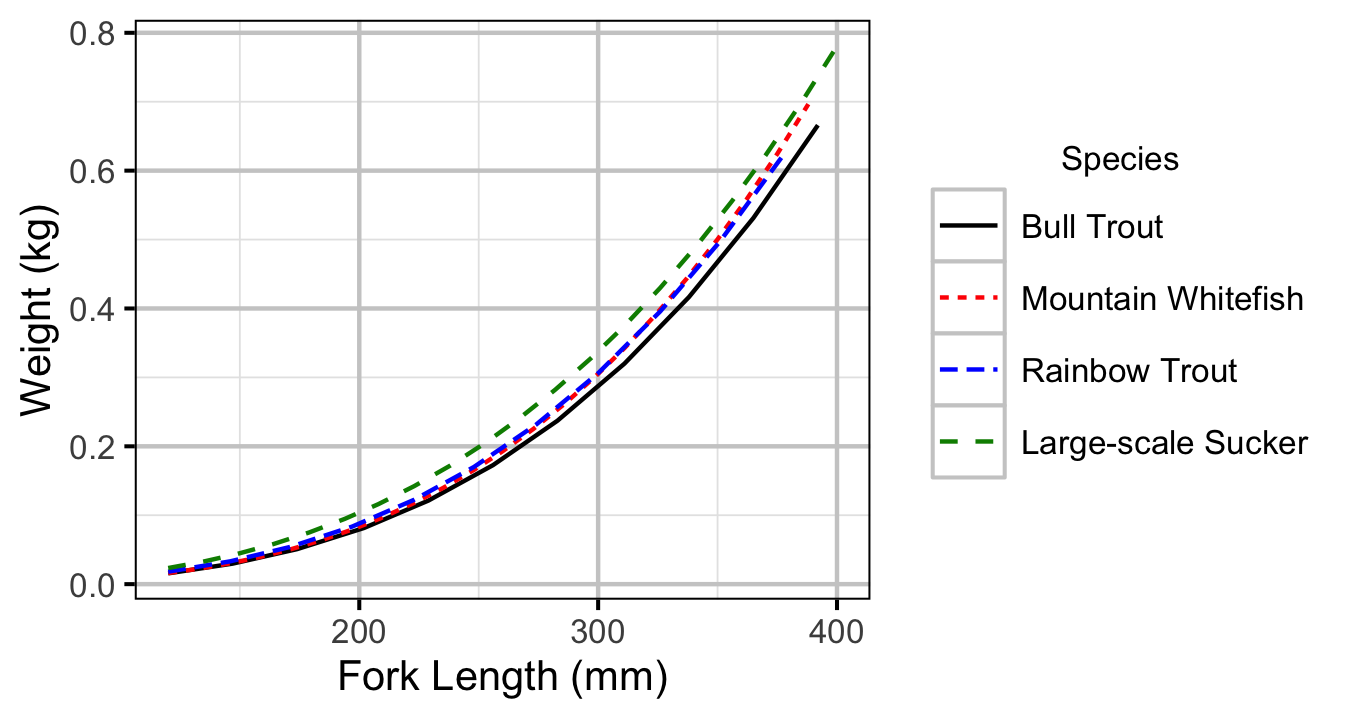
Figure 12. Predicted length-mass relationship by species.
Bull Trout
Juvenile
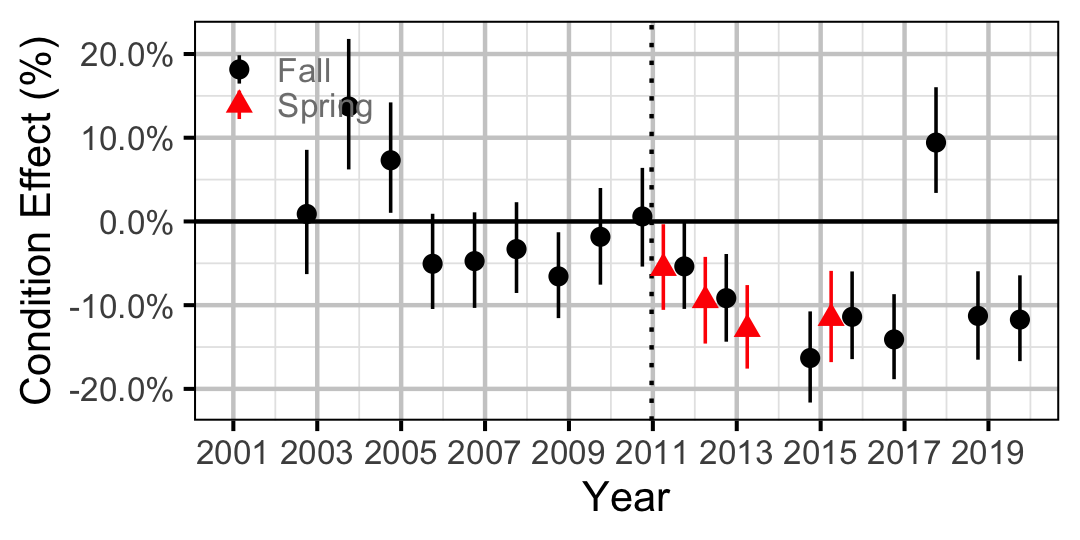
Figure 13. Body condition effect size estimates (with 95% CIs) by year for a 300 mm juvenile Bull Trout.
Adult
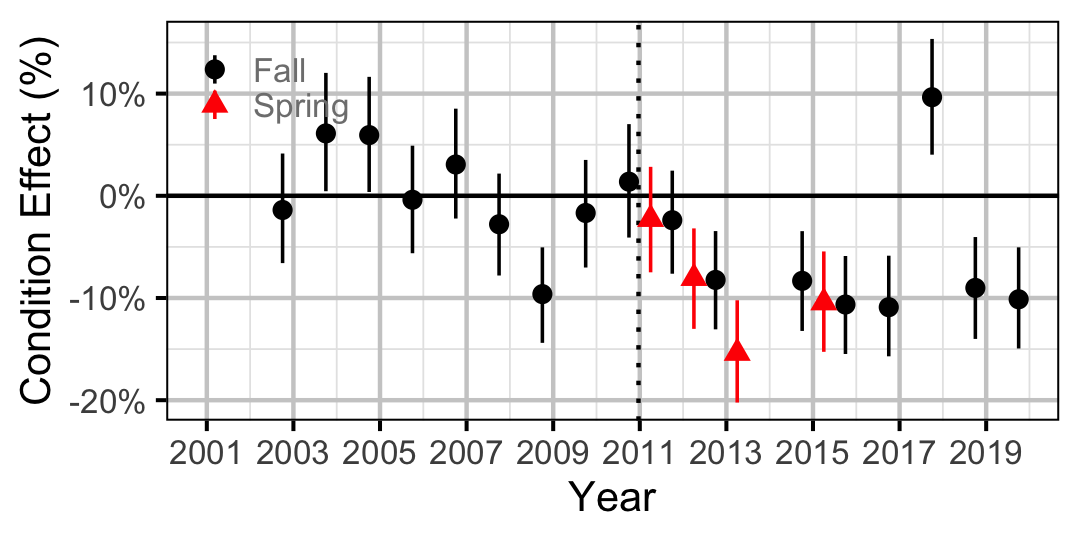
Figure 14. Body condition effect size estimates (with 95% CIs) by year for a 500 mm adult Bull Trout.
Mountain Whitefish
Juvenile
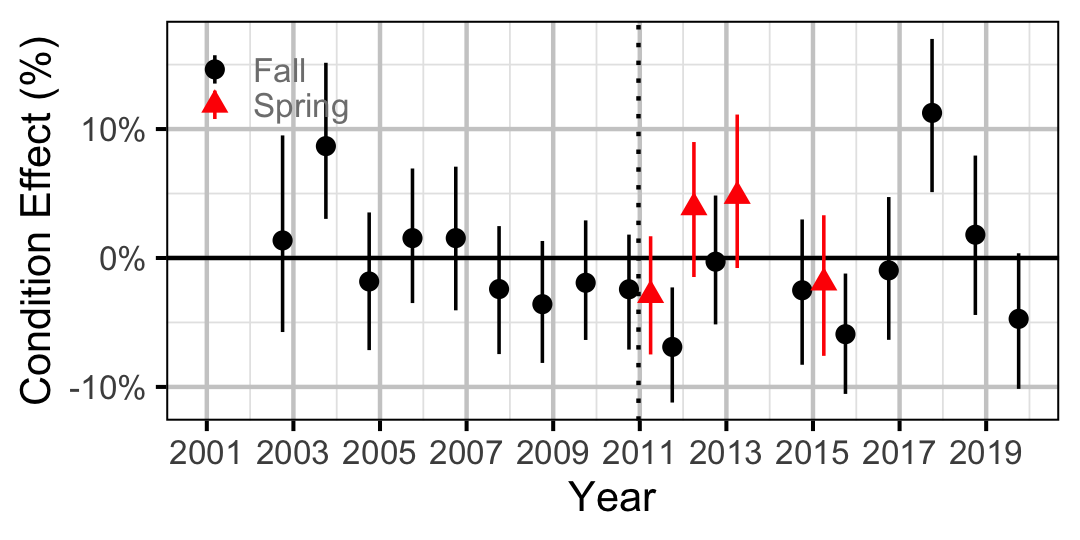
Figure 15. Body condition effect size estimates (with 95% CIs) by year for a 100 mm juvenile Mountain Whitefish.
Adult
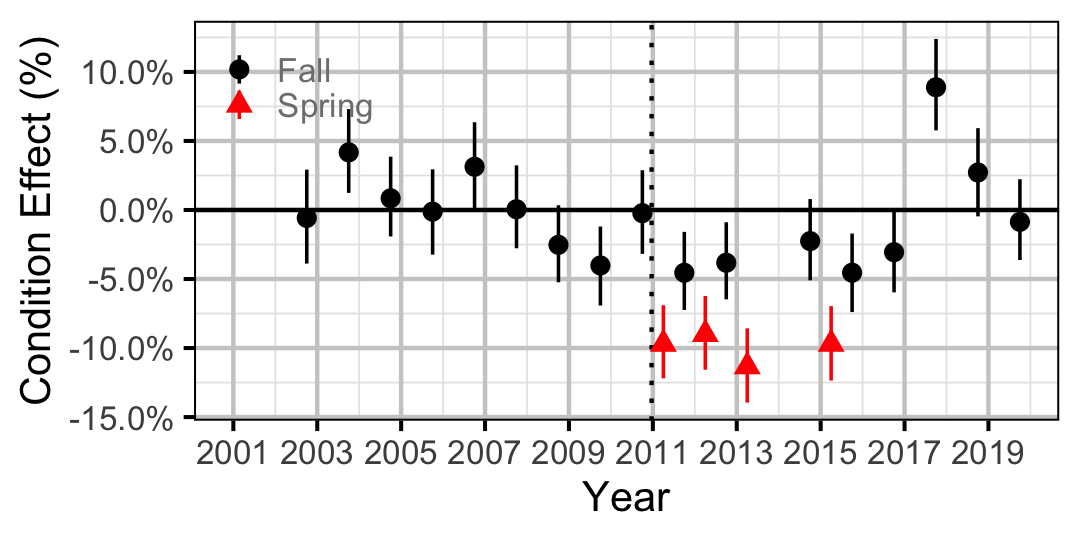
Figure 16. Body condition effect size estimates (with 95% CIs) by year for a 250 mm adult Mountain Whitefish.
Rainbow Trout
Juvenile
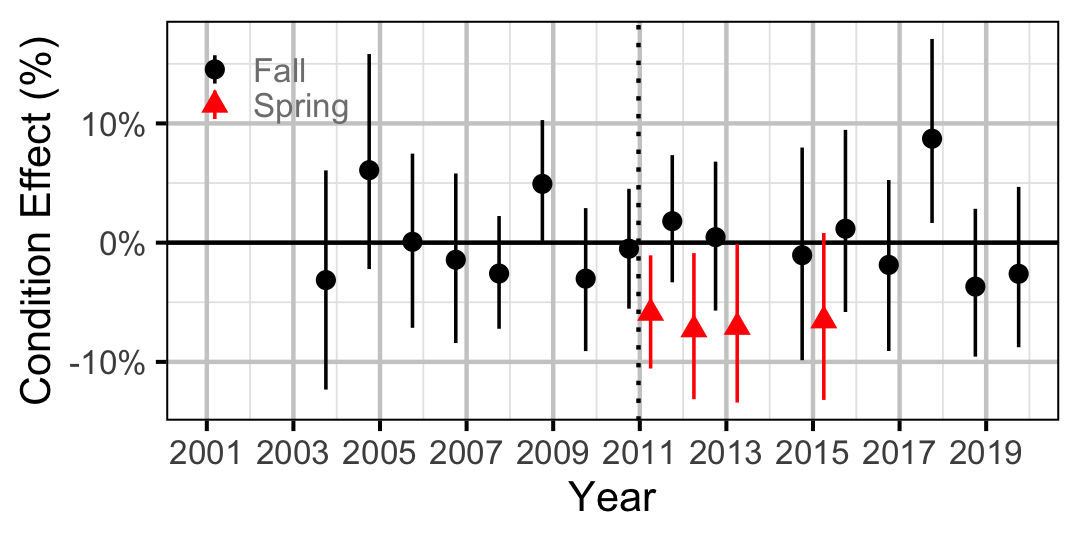
Figure 17. Body condition effect size estimates (with 95% CIs) by year for a 150 mm juvenile Rainbow Trout.
Adult
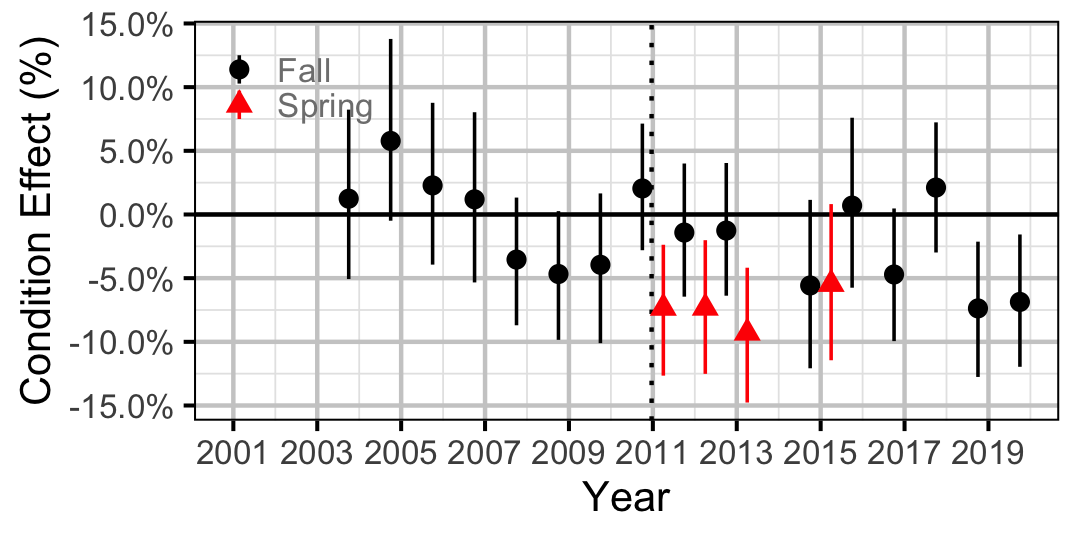
Figure 18. Body condition effect size estimates (with 95% CIs) by year for a 300 mm adult Rainbow Trout.
Largescale Sucker
Juvenile
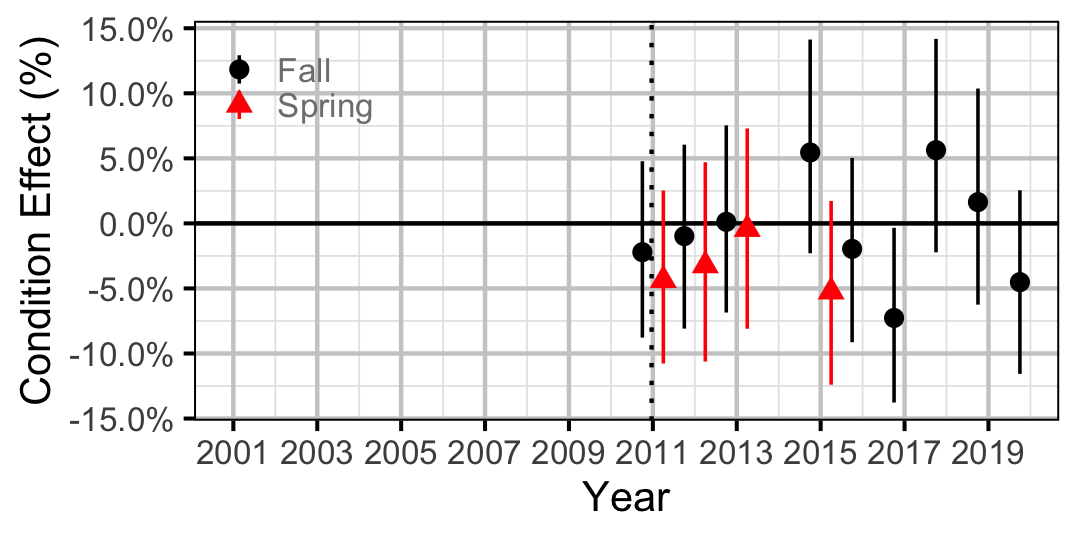
Figure 19. Body condition effect size estimates (with 95% CIs) by year for a 300 mm juvenile Largescale Sucker.
Adult
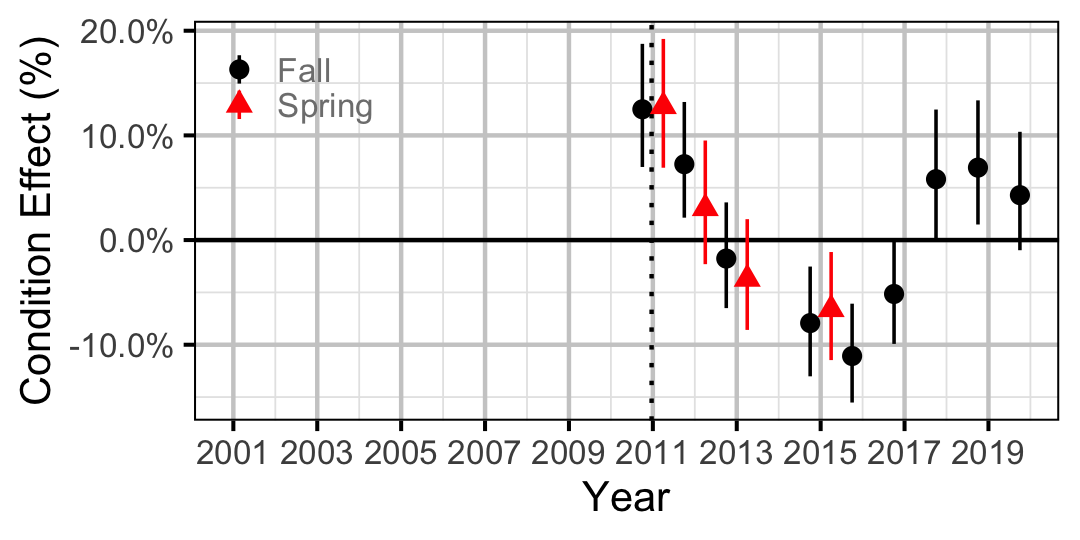
Figure 20. Body condition effect size estimates (with 95% CIs) by year for a 500 mm adult Largescale Sucker.
Occupancy
Rainbow Trout
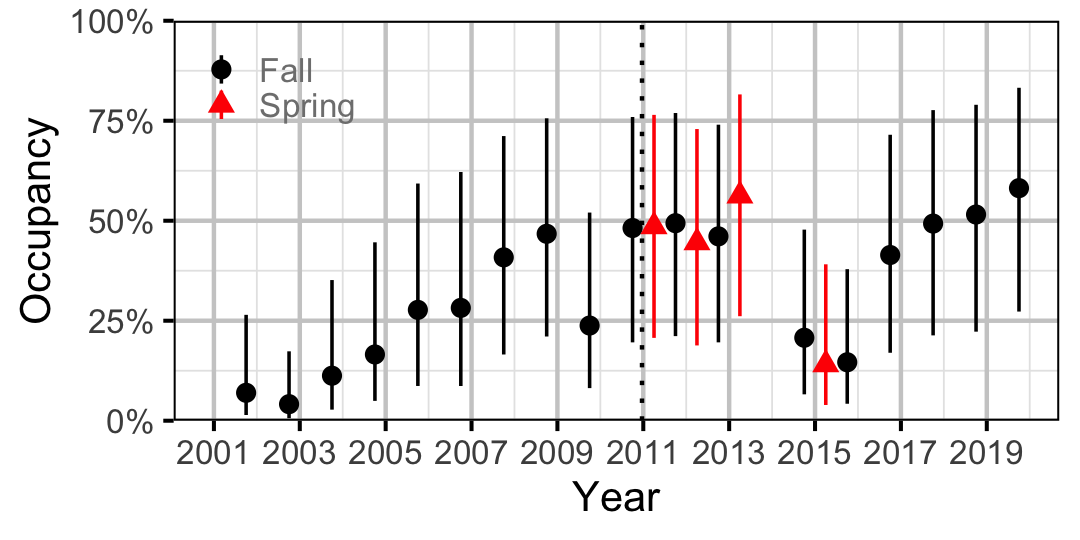
Figure 21. Estimated occupancy of Rainbow Trout at a typical site by year (with 95% CIs).
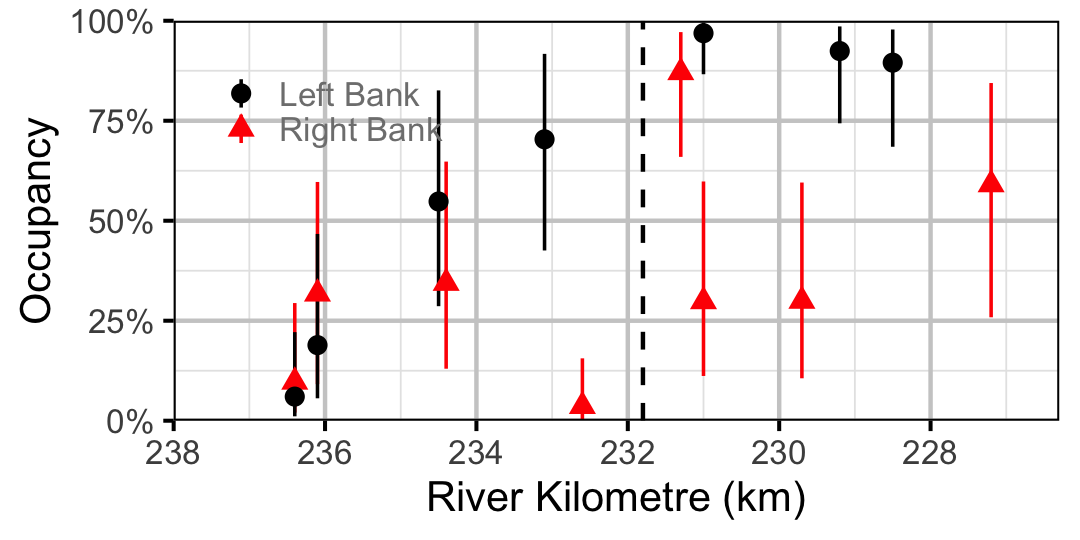
Figure 22. Estimated occupancy of Rainbow Trout in 2010 by site (with 95% CIs).
Burbot
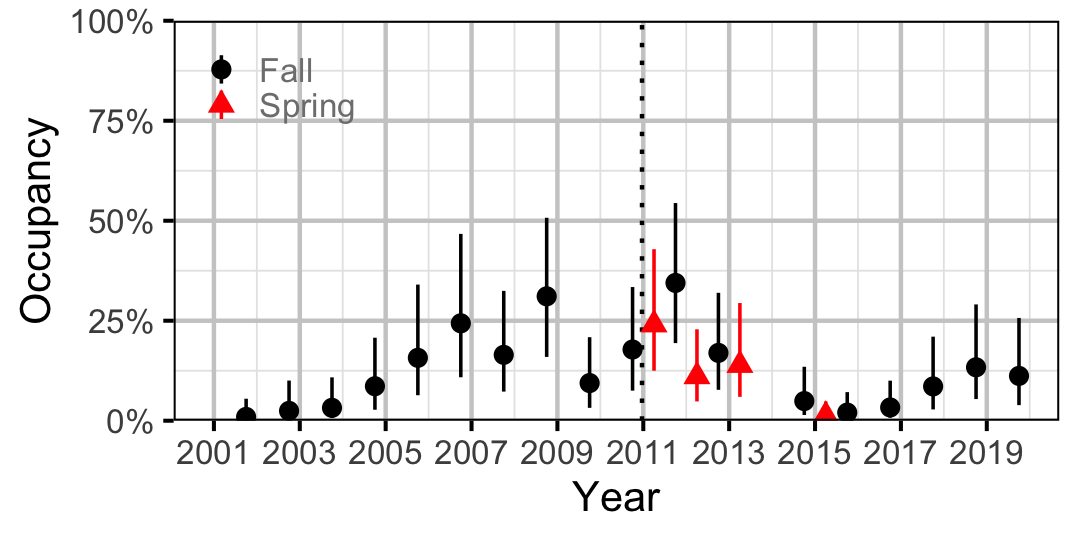
Figure 23. Estimated occupancy of Burbot at a typical site by year (with 95% CIs).
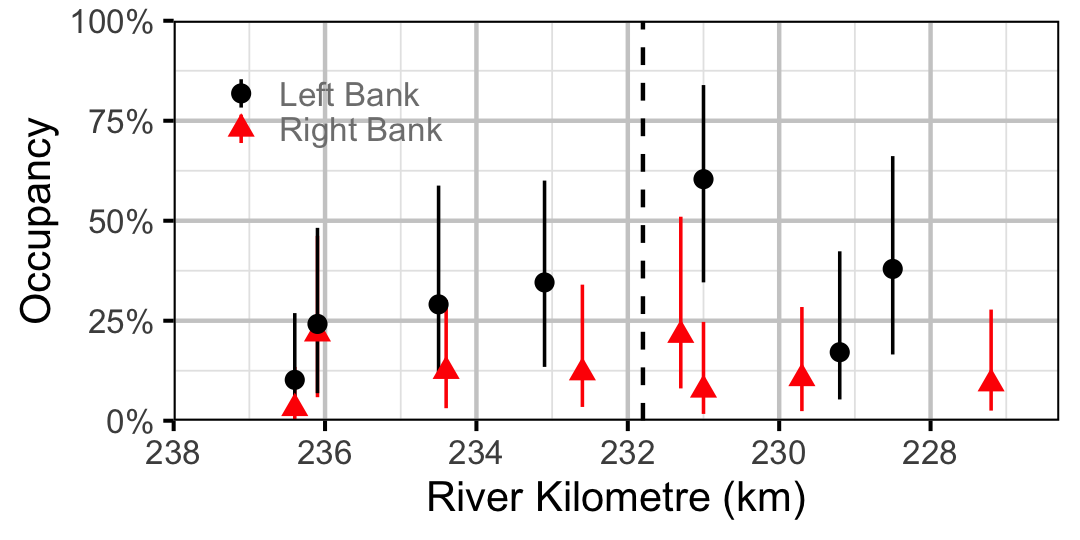
Figure 24. Estimated occupancy of Burbot in 2010 by site (with 95% CIs).
Lake Whitefish
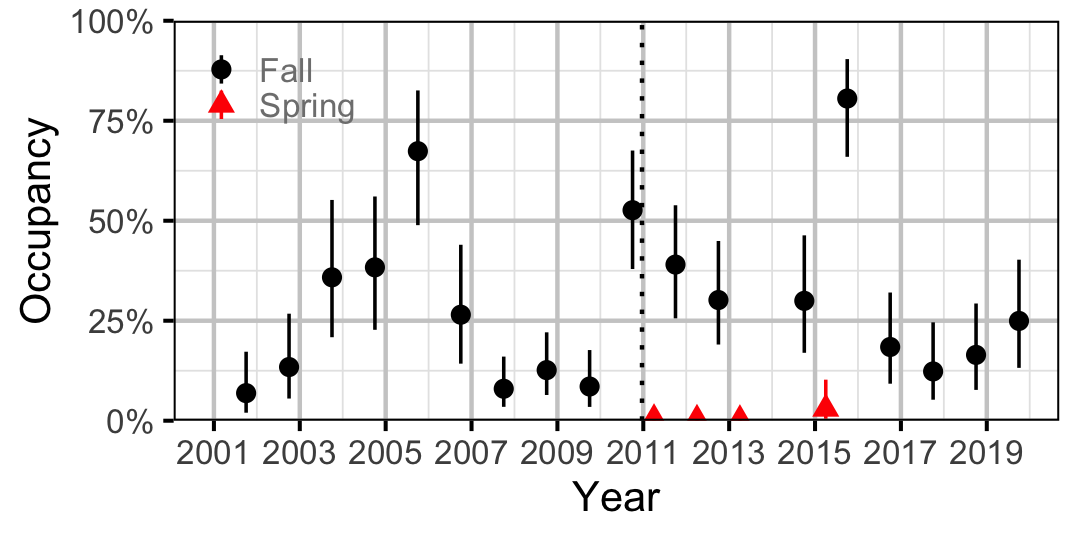
Figure 25. Estimated occupancy of Lake Whitefish at a typical site by year (with 95% CIs).
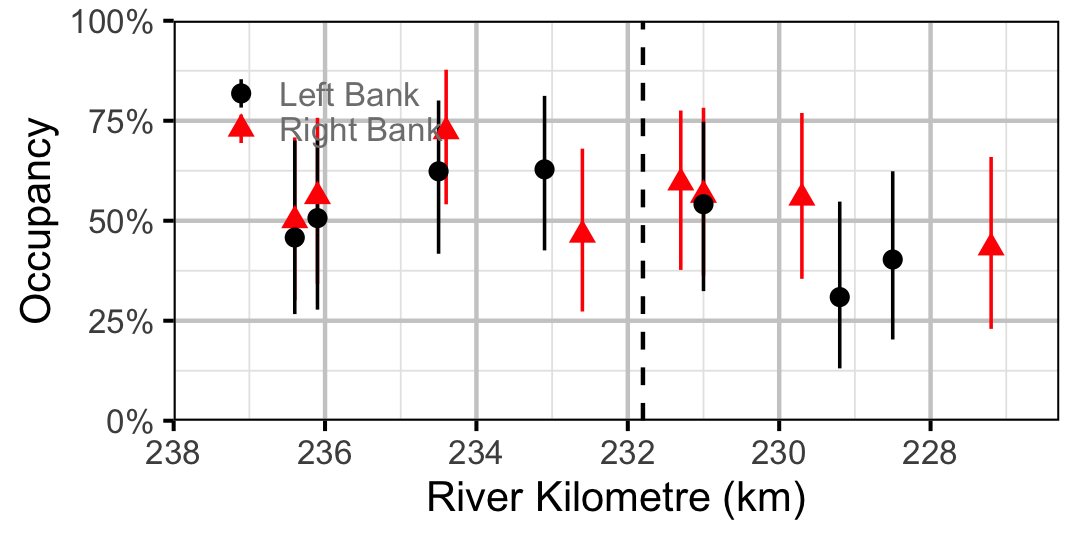
Figure 26. Estimated occupancy of Lake Whitefish in 2010 by site (with 95% CIs).
Northern Pikeminnow
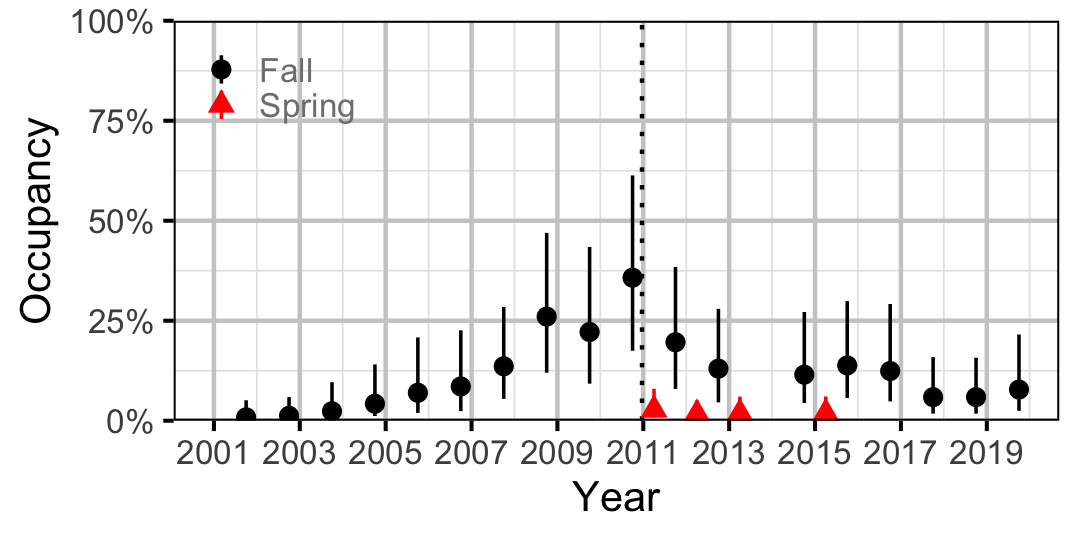
Figure 27. Estimated occupancy of Northern Pikeminnow at a typical site by year (with 95% CIs).
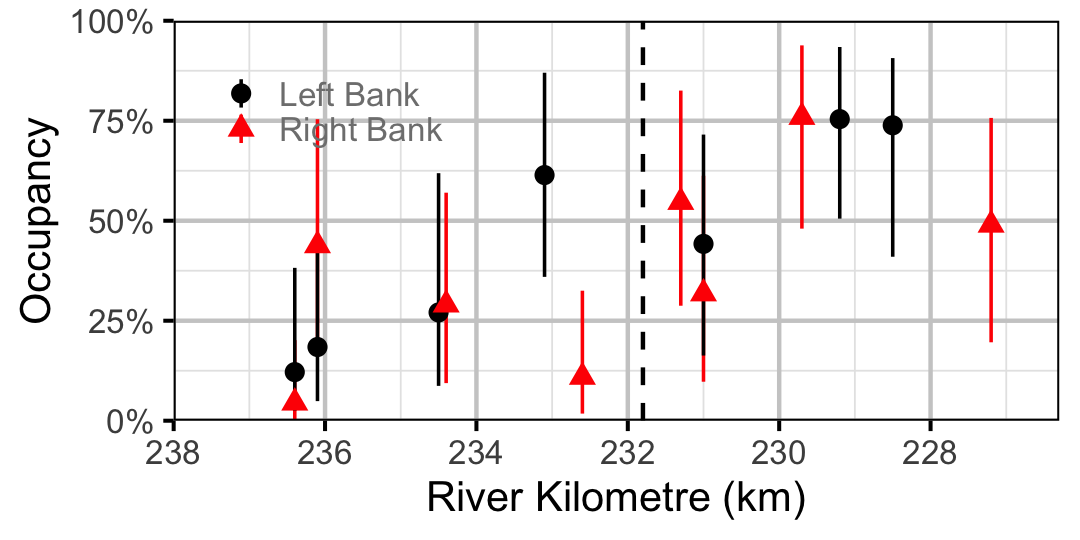
Figure 28. Estimated occupancy of Northern Pikeminnow in 2010 by site (with 95% CIs).
Redside Shiner
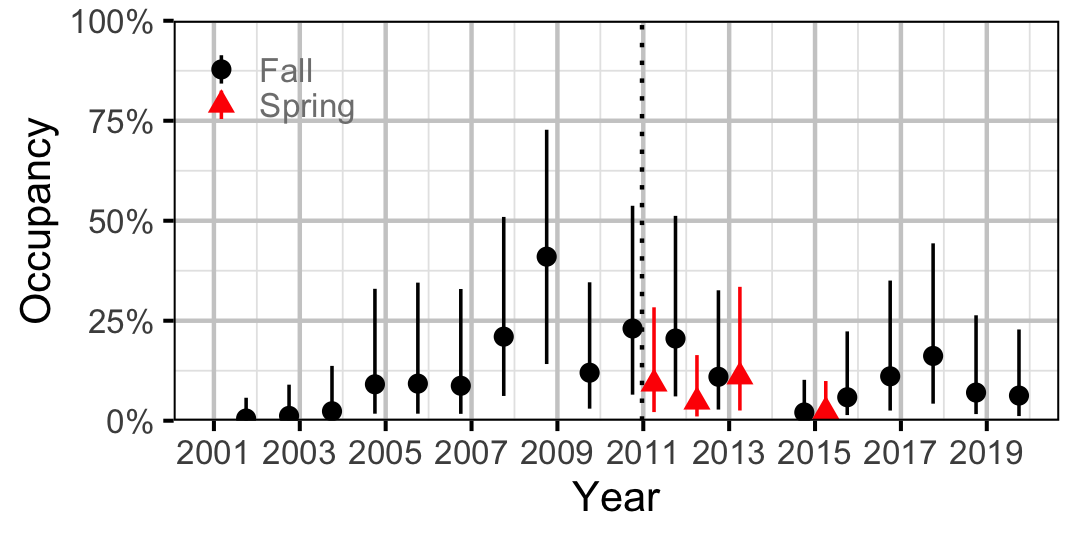
Figure 29. Estimated occupancy of Redside Shiner at a typical site by year (with 95% CIs).
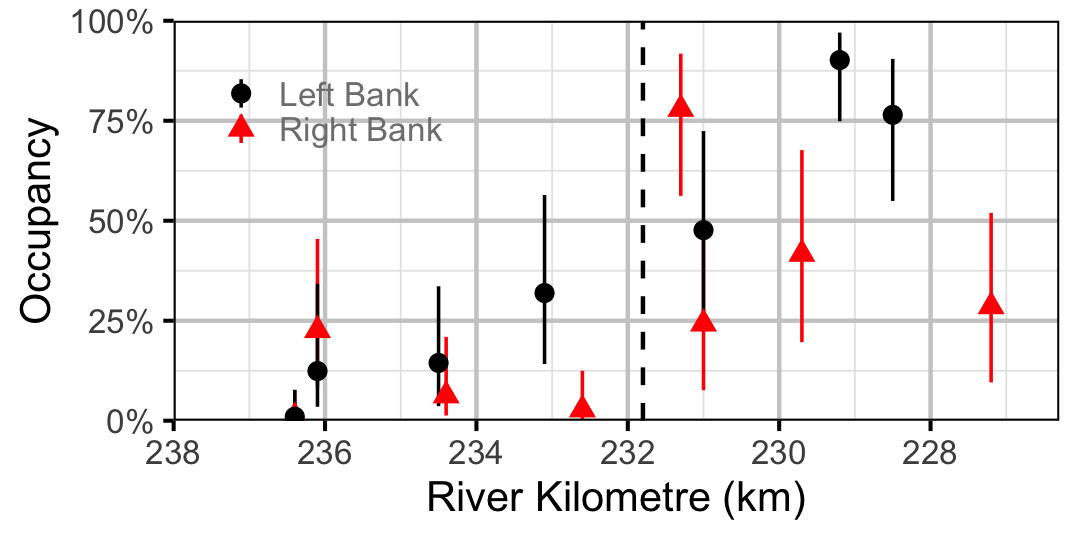
Figure 30. Estimated occupancy of Redside Shiner in 2010 by site (with 95% CIs).
Sculpins
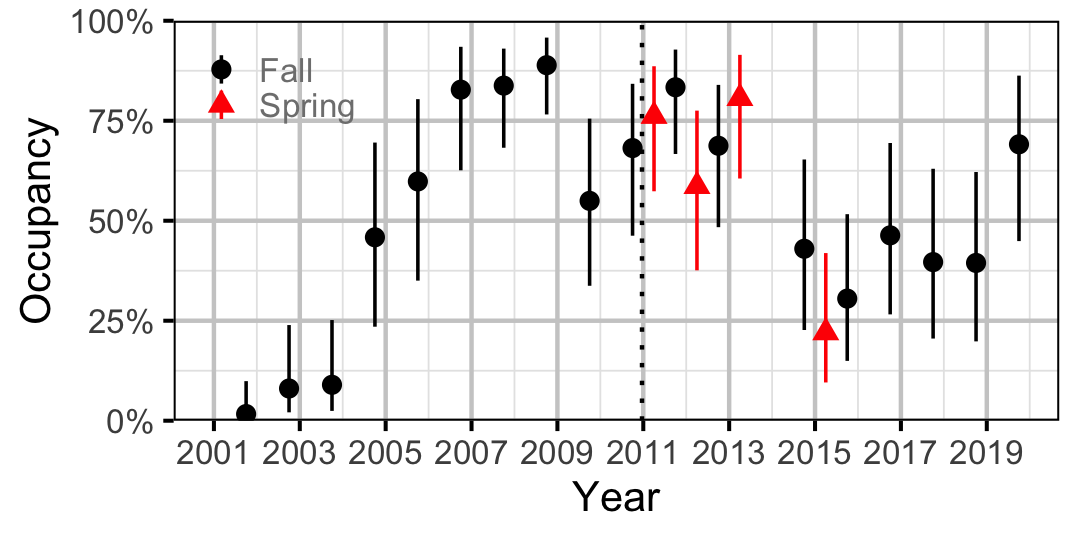
Figure 31. Estimated occupancy of Sculpins at a typical site by year (with 95% CIs).
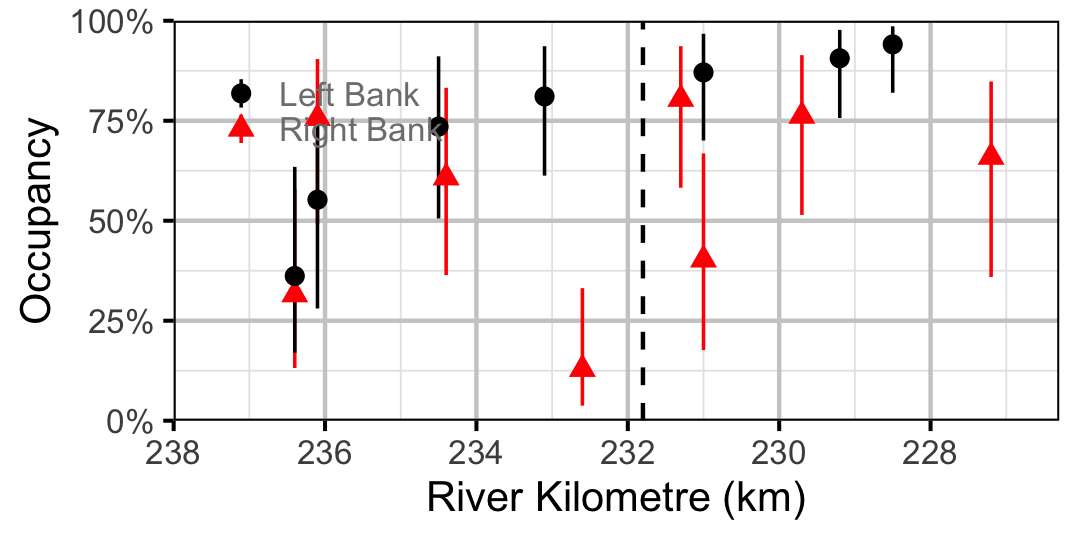
Figure 32. Estimated occupancy of Sculpins in 2010 by site (with 95% CIs).
Count
Rainbow Trout
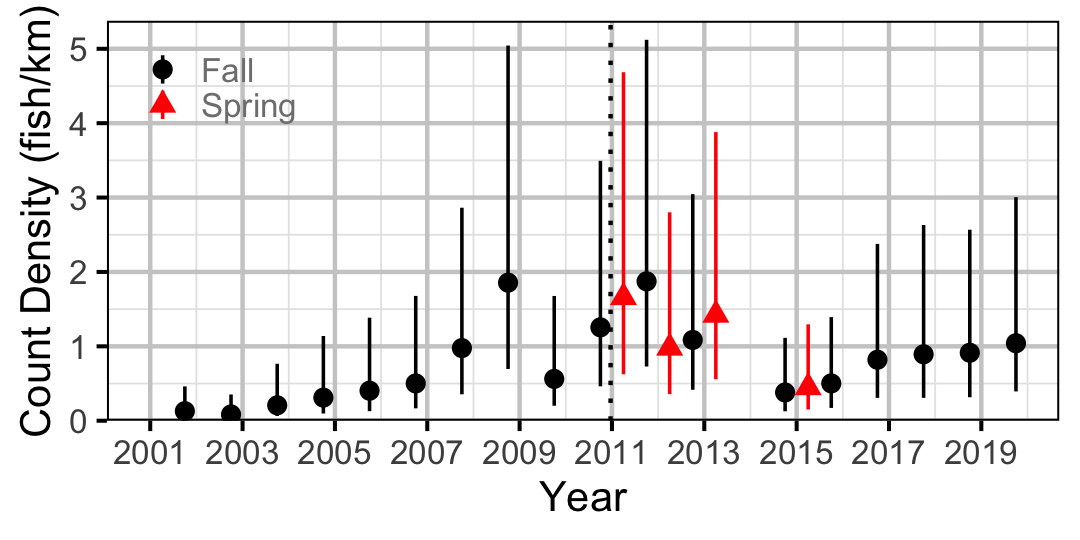
Figure 33. Estimated lineal river count density of Rainbow Trout by year (with 95% CIs).
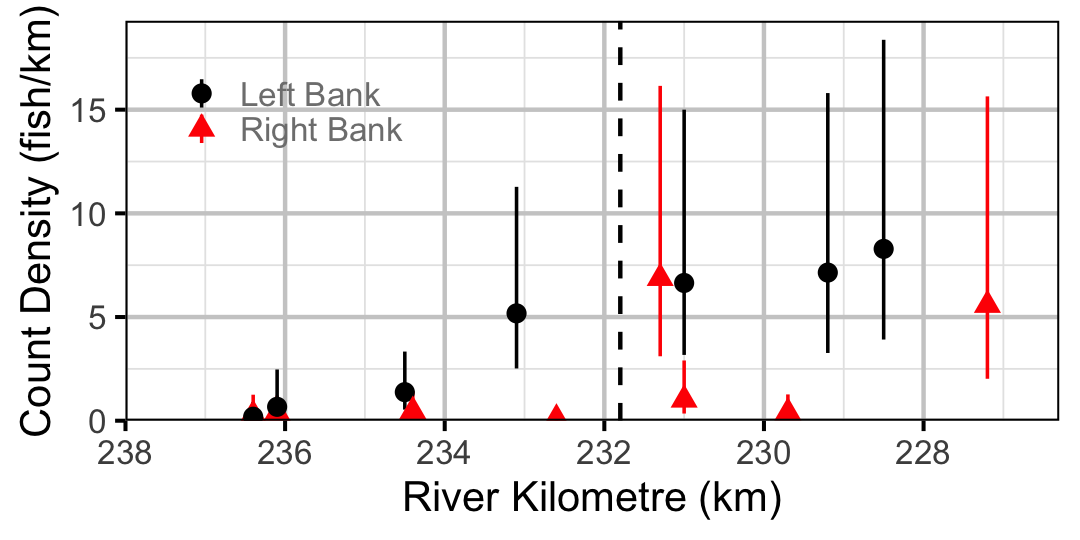
Figure 34. Estimated lineal river count density of Rainbow Trout by site in 2010 (with 95% CIs).
Burbot
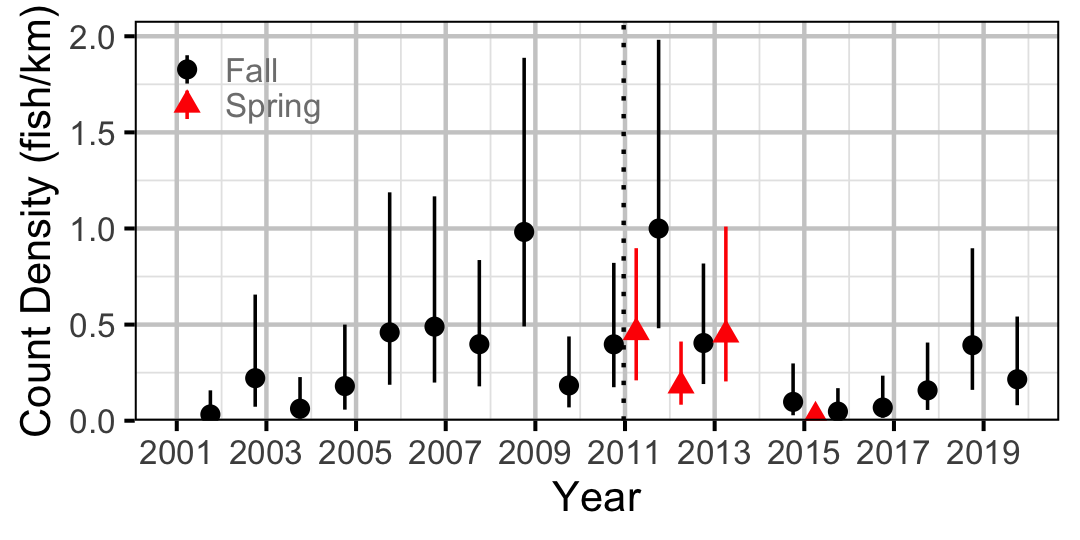
Figure 35. Estimated lineal river count density of Burbot by year (with 95% CIs).
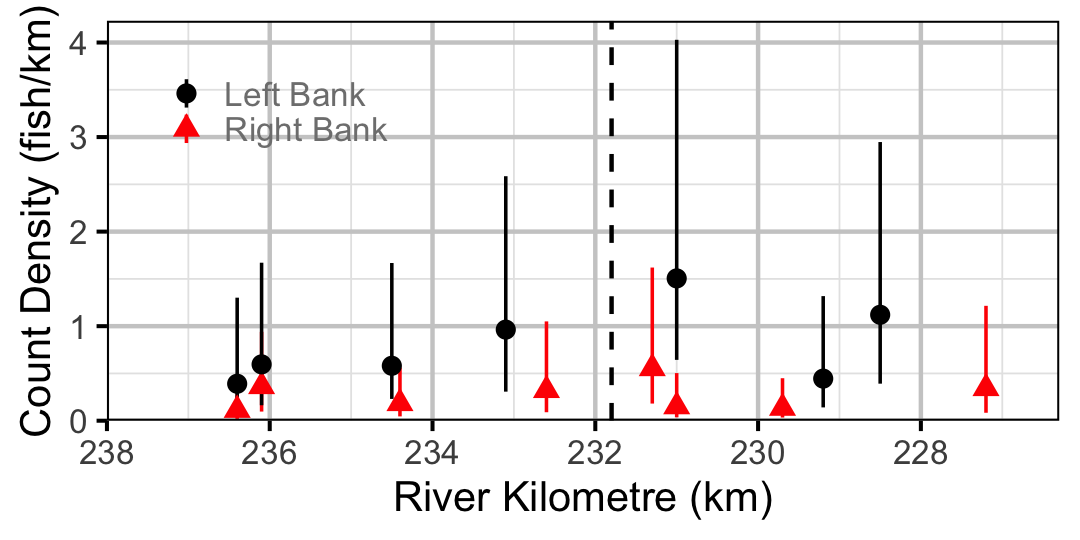
Figure 36. Estimated lineal river count density of Burbot by site in 2010 (with 95% CIs).
Northern Pikeminnow
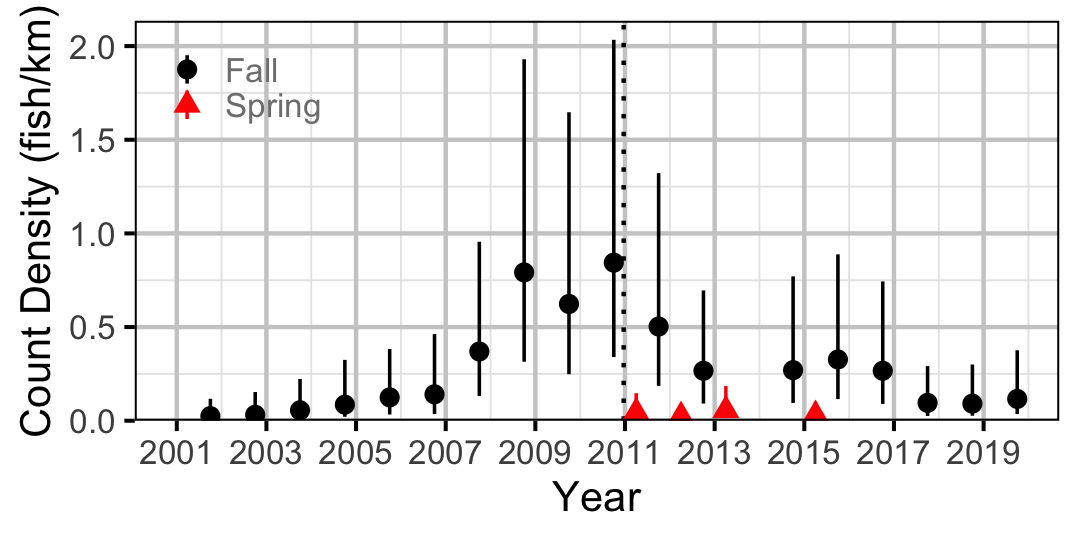
Figure 37. Estimated lineal river count density of Northern Pikeminnow by year (with 95% CIs).
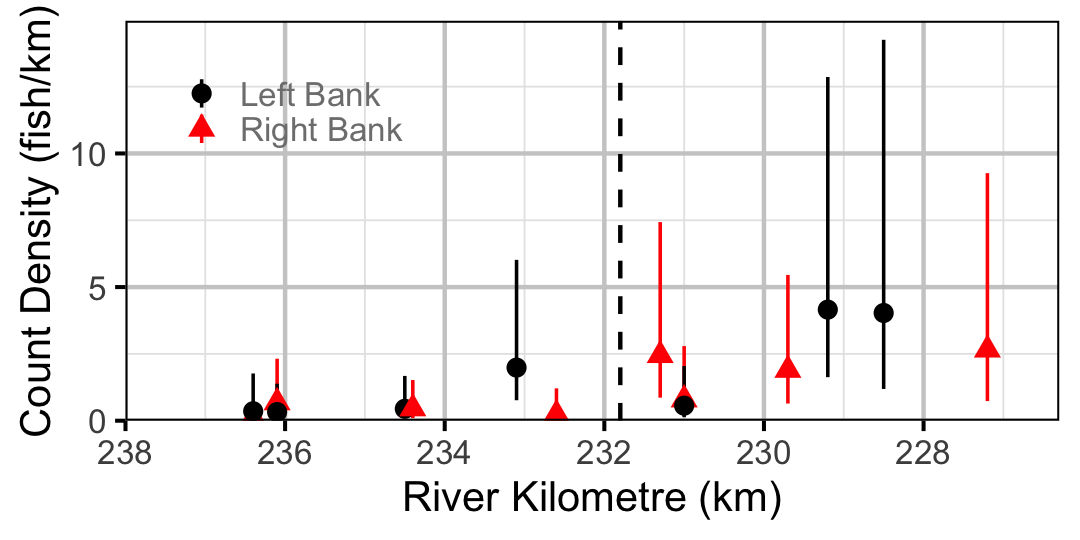
Figure 38. Estimated lineal river count density of Northern Pikeminnow by site in 2010 (with 95% CIs).
Suckers
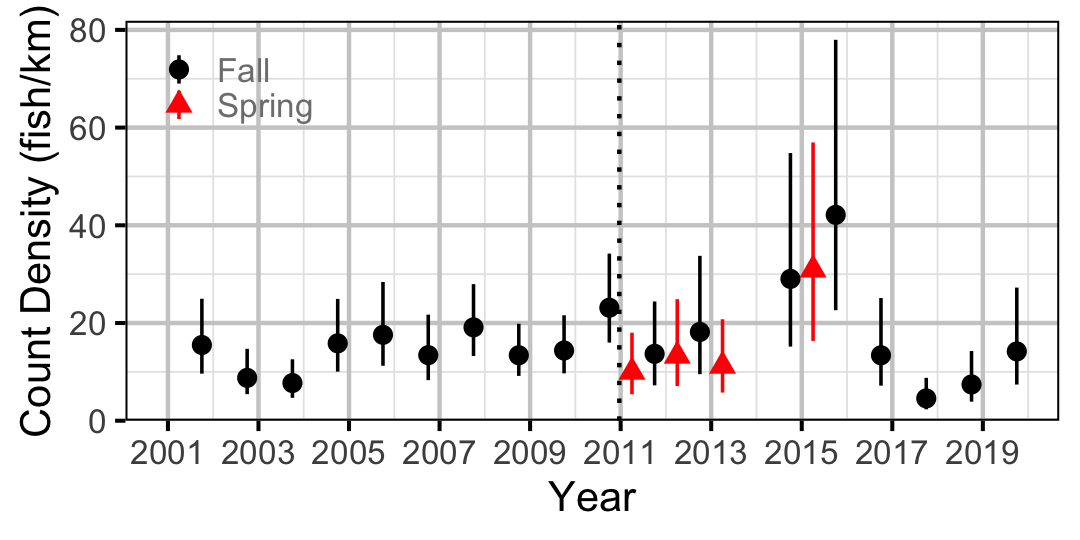
Figure 39. Estimated lineal river count density of Sucker by year (with 95% CIs).
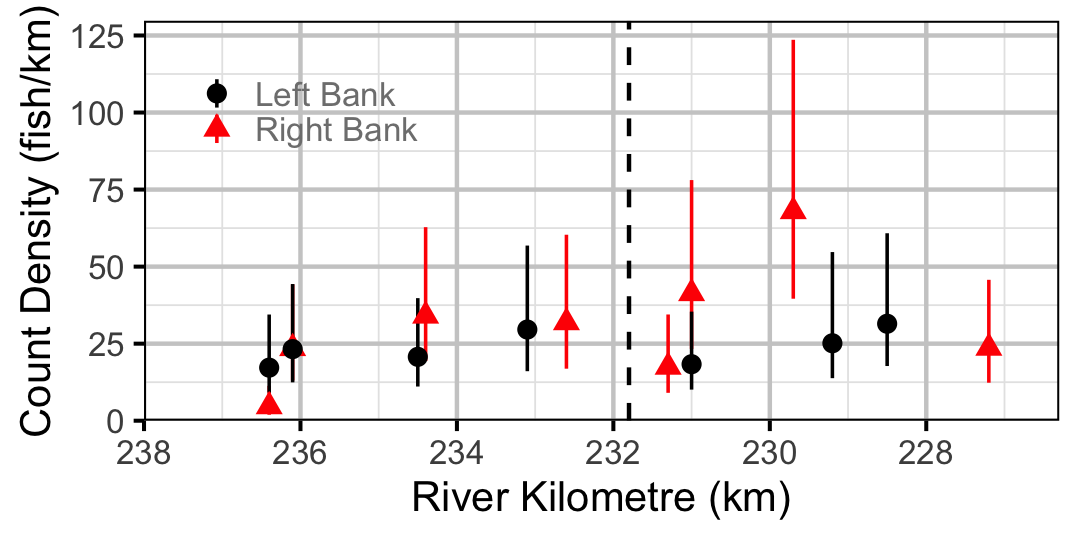
Figure 40. Estimated lineal river count density of Sucker by site in 2010 (with 95% CIs).
Movement
Bull Trout
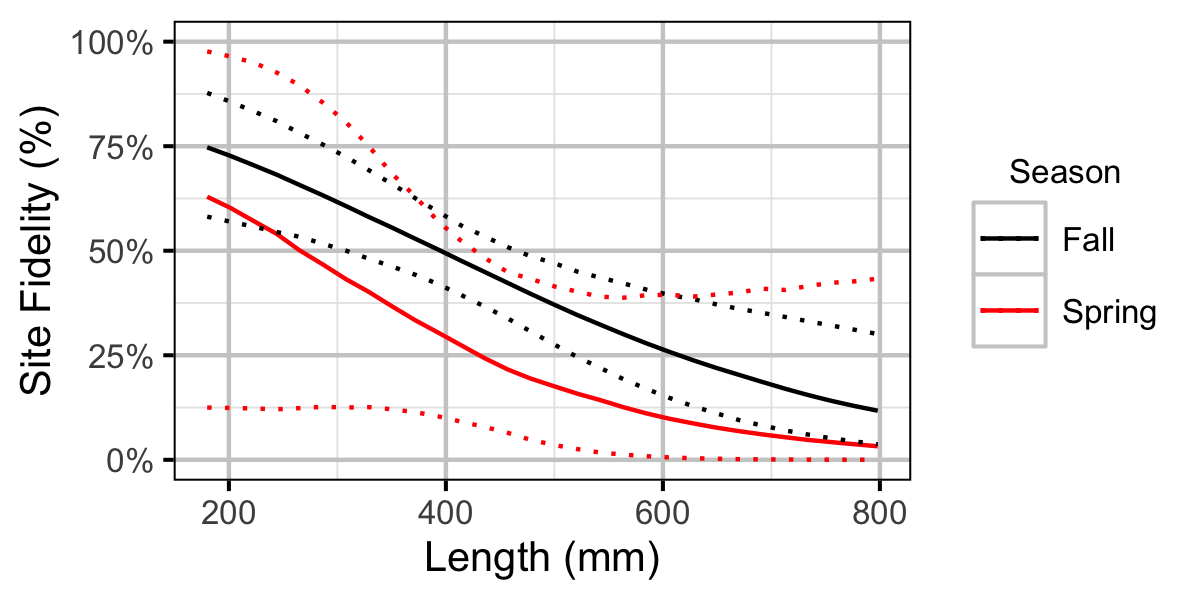
Figure 41. Probability of recapture at the same site versus a different site by fish length and season (with 95% CIs).
Mountain Whitefish
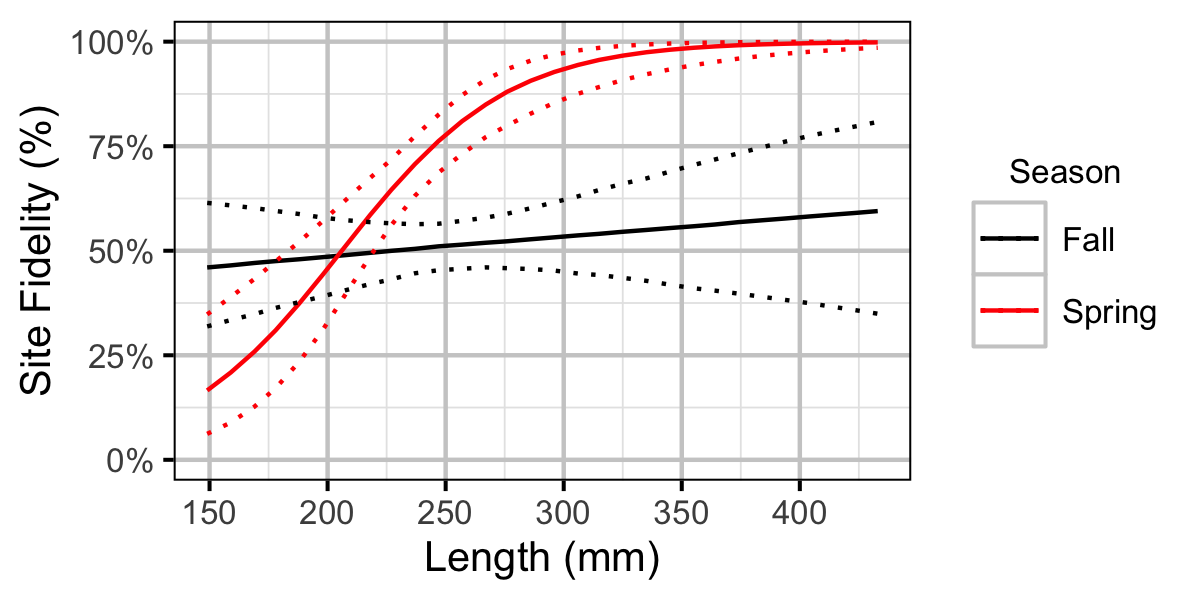
Figure 42. Probability of recapture at the same site versus a different site by fish length and season (with 95% CIs).
Rainbow Trout
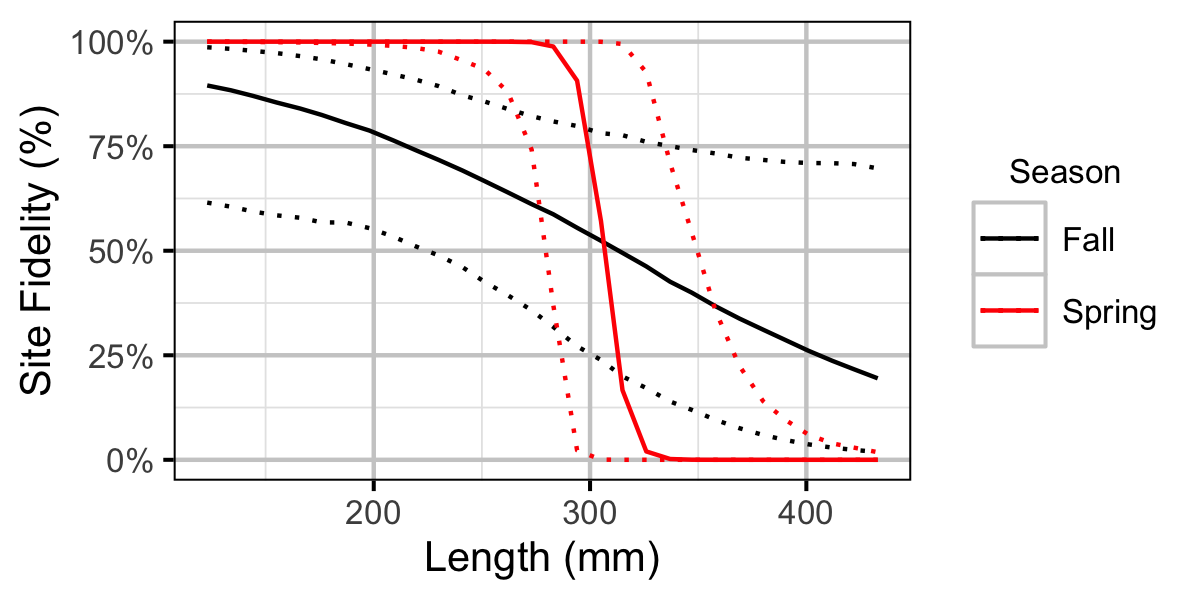
Figure 43. Probability of recapture at the same site versus a different site by fish length and season (with 95% CIs).
Largescale Sucker
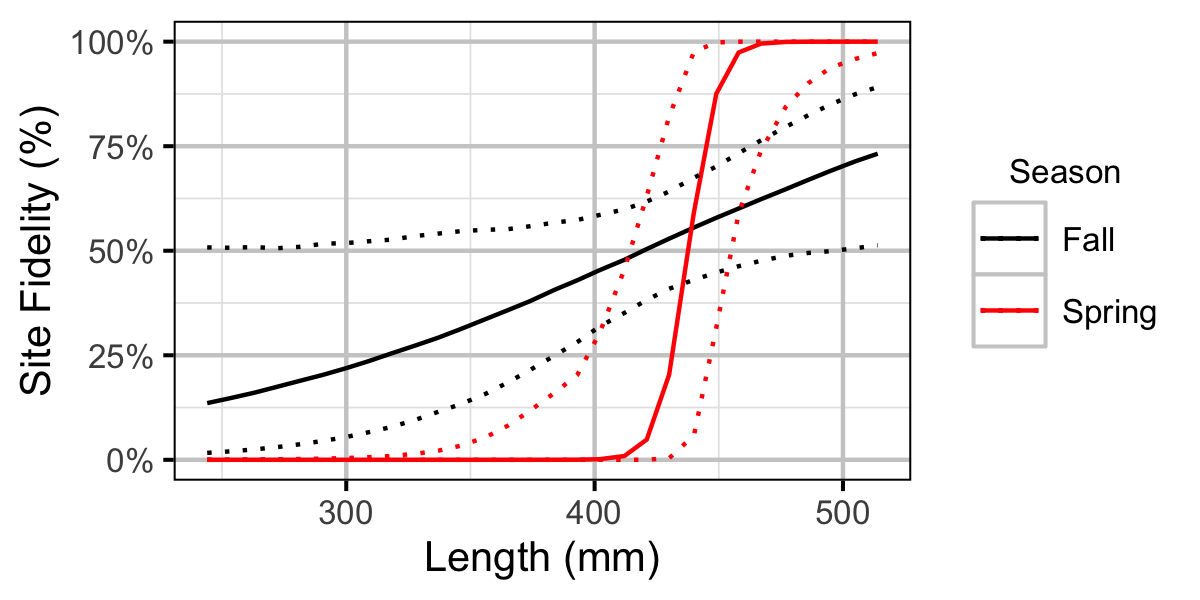
Figure 44. Probability of recapture at the same site versus a different site by fish length and season (with 95% CIs).
Observer Length Correction
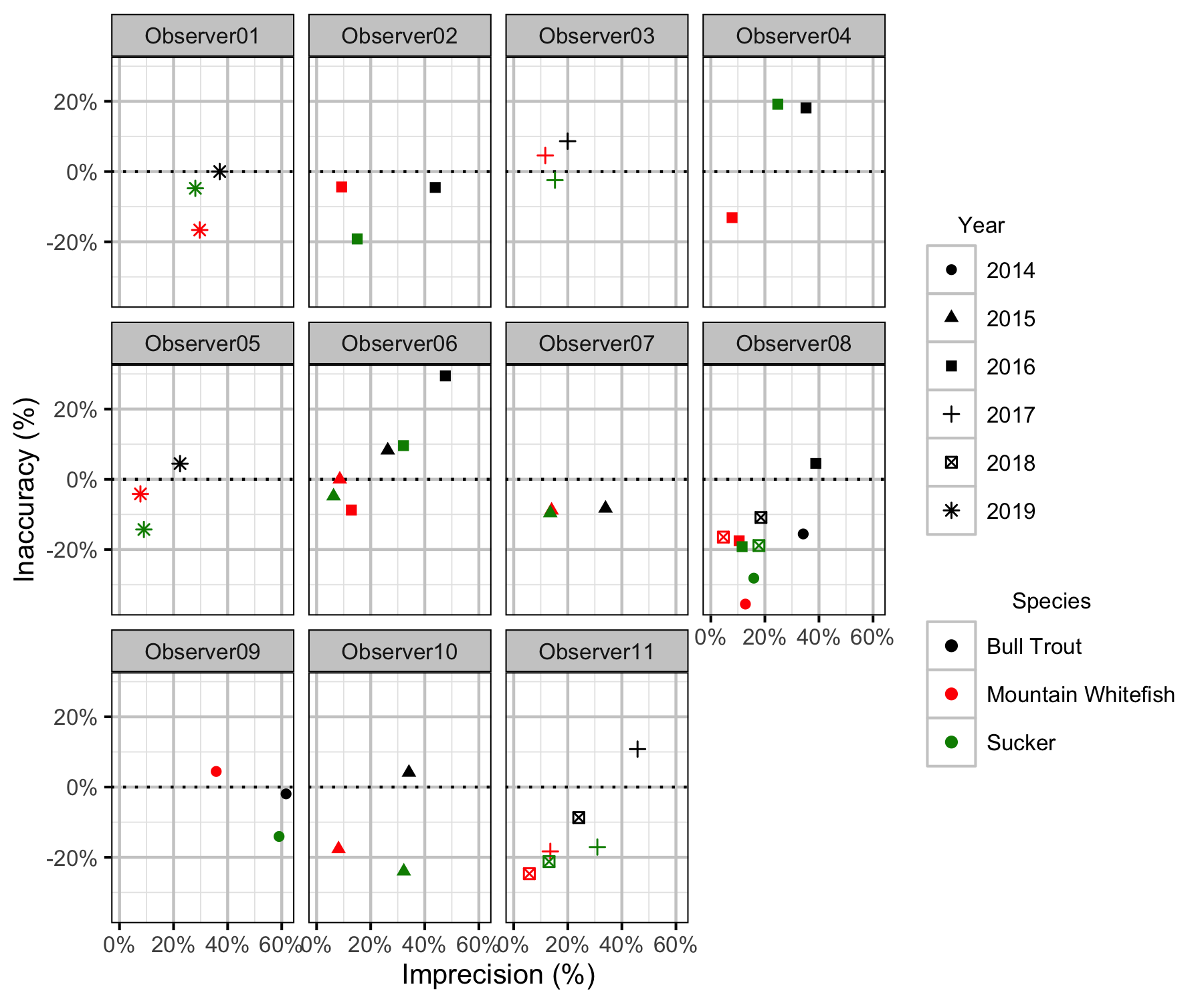
Figure 45. Length inaccuracy and imprecision by observer, year and species.
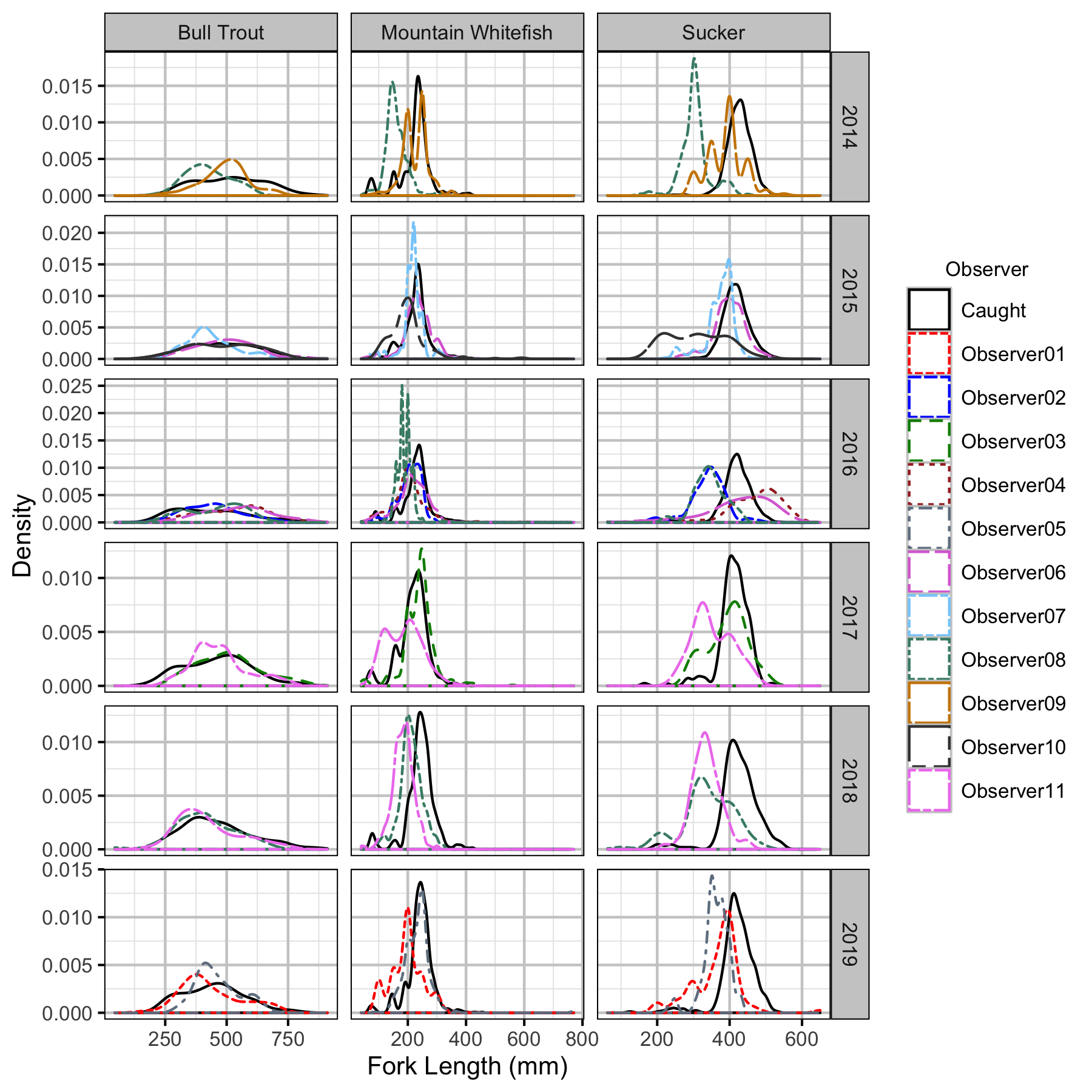
Figure 46. Observed length density plots by species, year and observer.
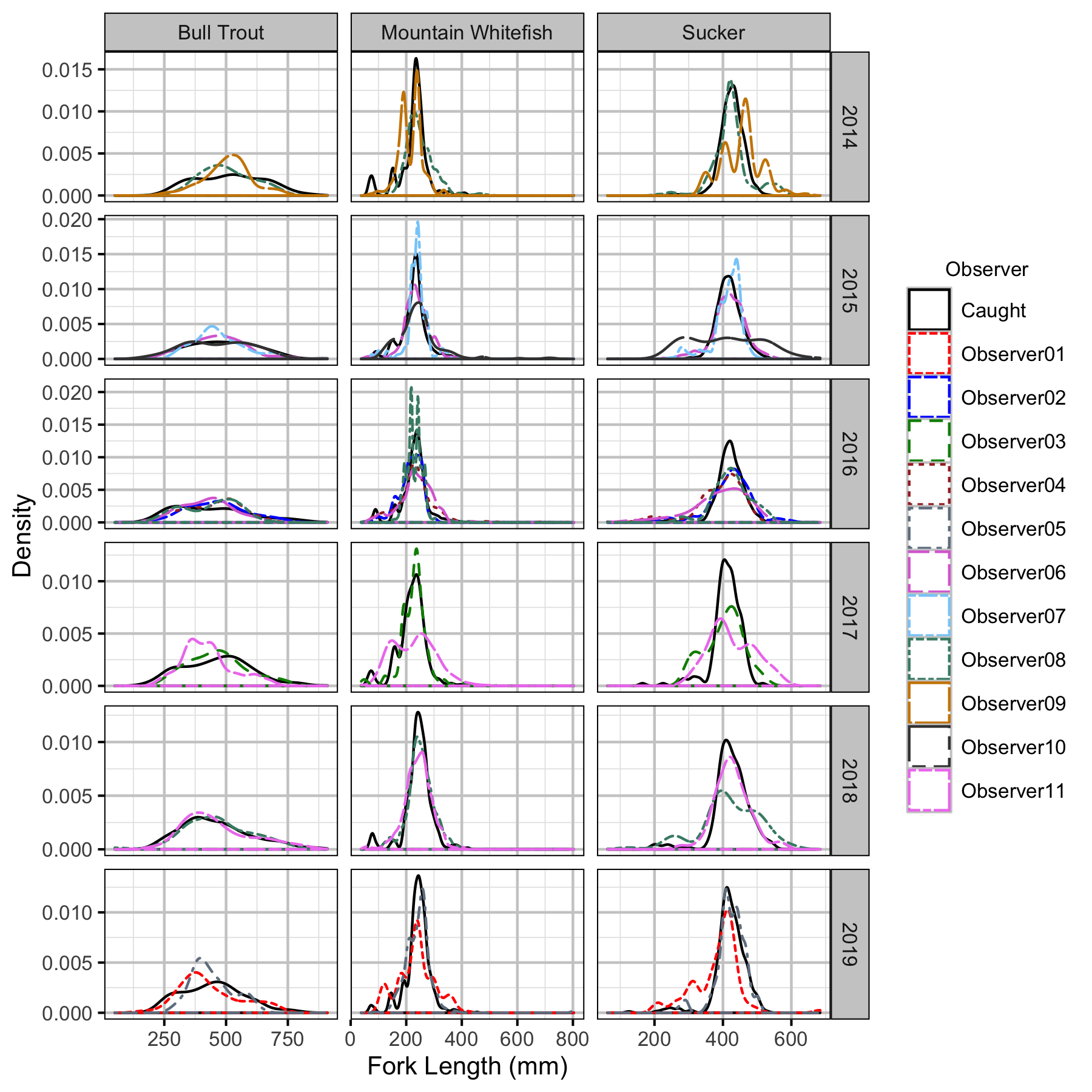
Figure 47. Corrected length density plots by species, year and observer.
Abundance
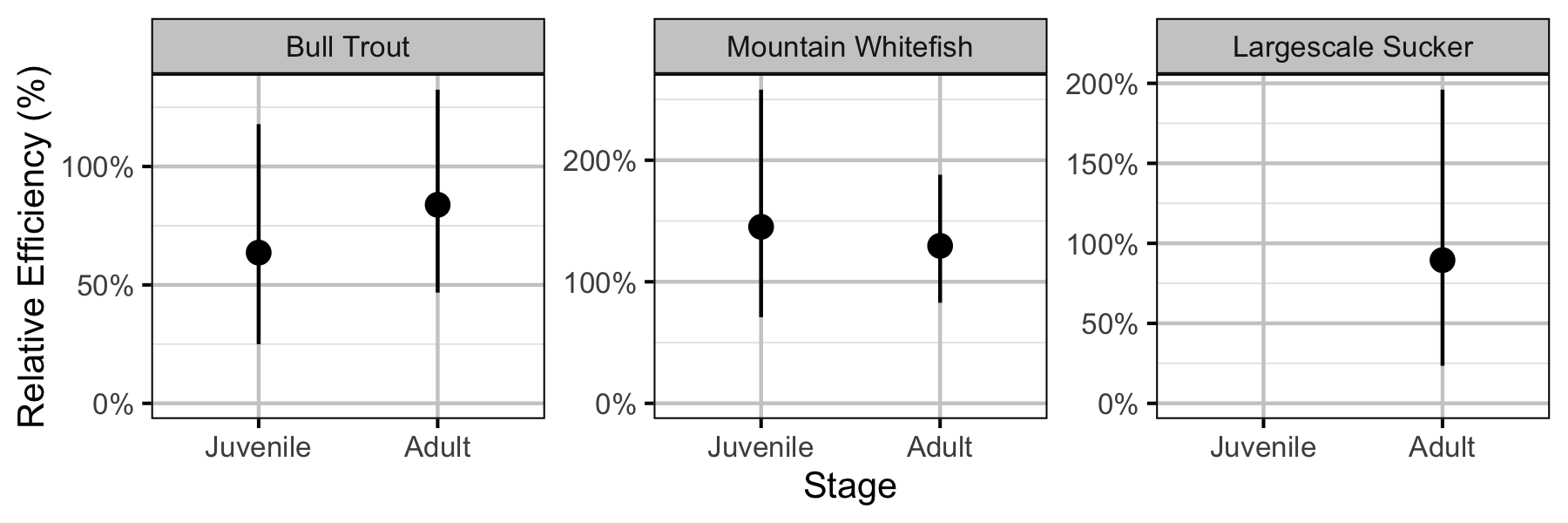
Figure 48. Effect of counting (versus capture) on encounter efficiency by species and stage (with 95% CIs).
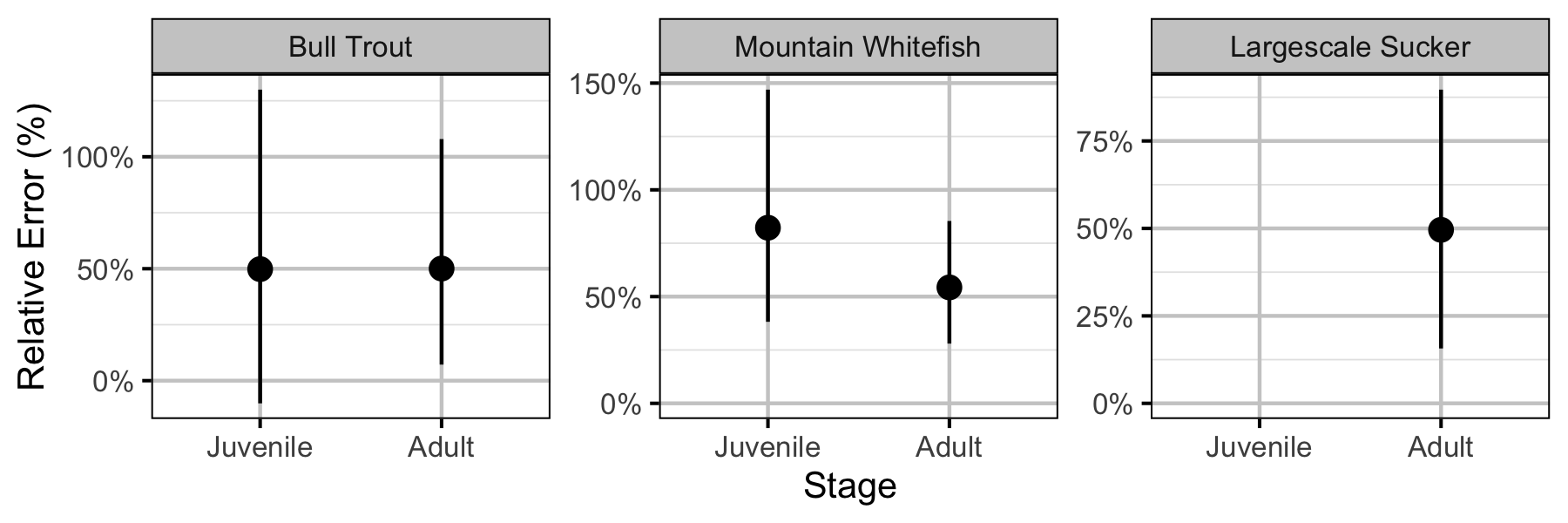
Figure 49. Effect of counting (versus capture) on overdispersion efficiency by species and stage (with 95% CIs).
Bull Trout
Juvenile
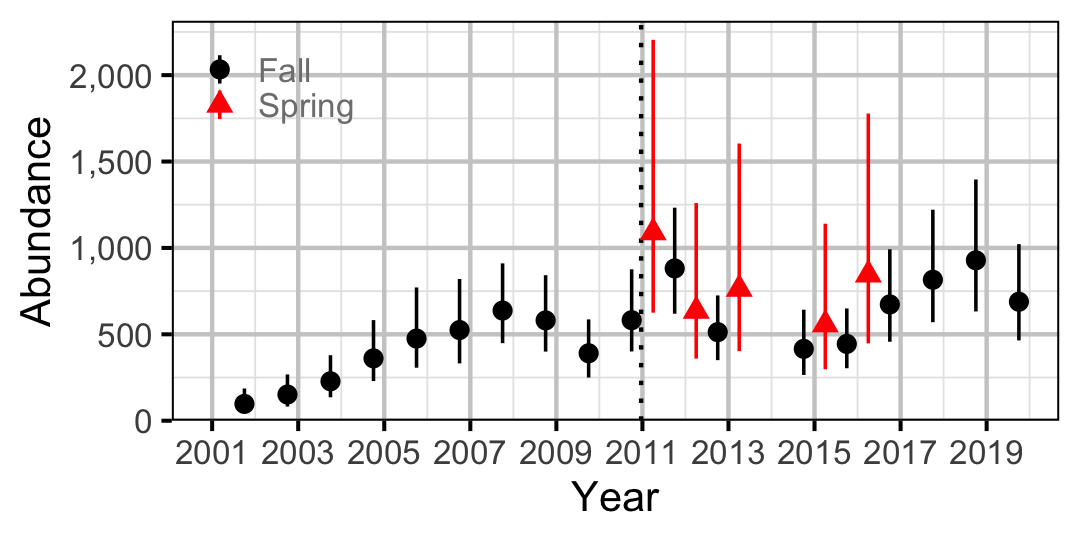
Figure 50. Abundance of Juvenile Bull Trout by year (with 95% CIs).
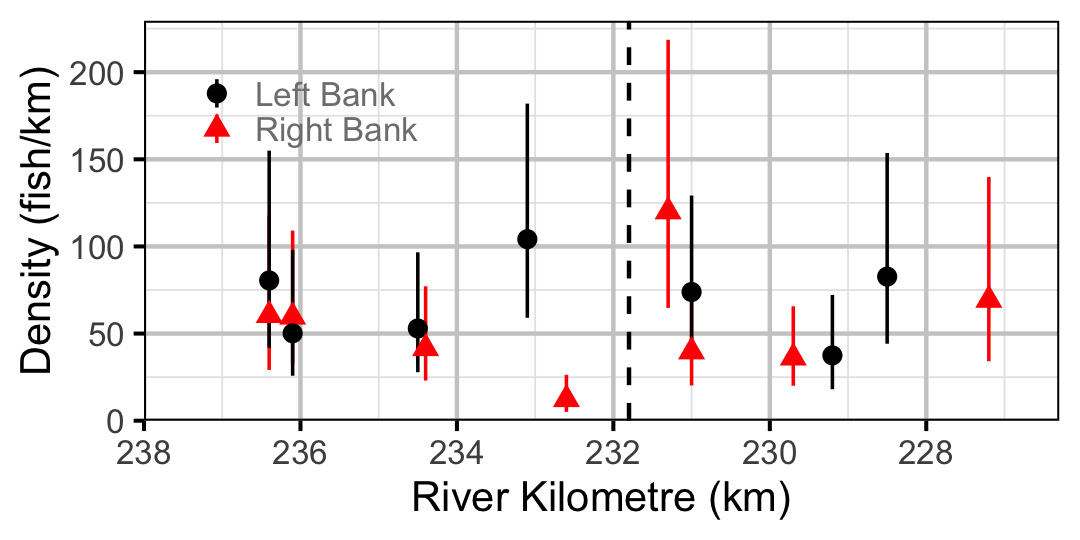
Figure 51. Estimated lineal river count density of Juvenile Bull Trout by site in 2010(with 95% CIs).
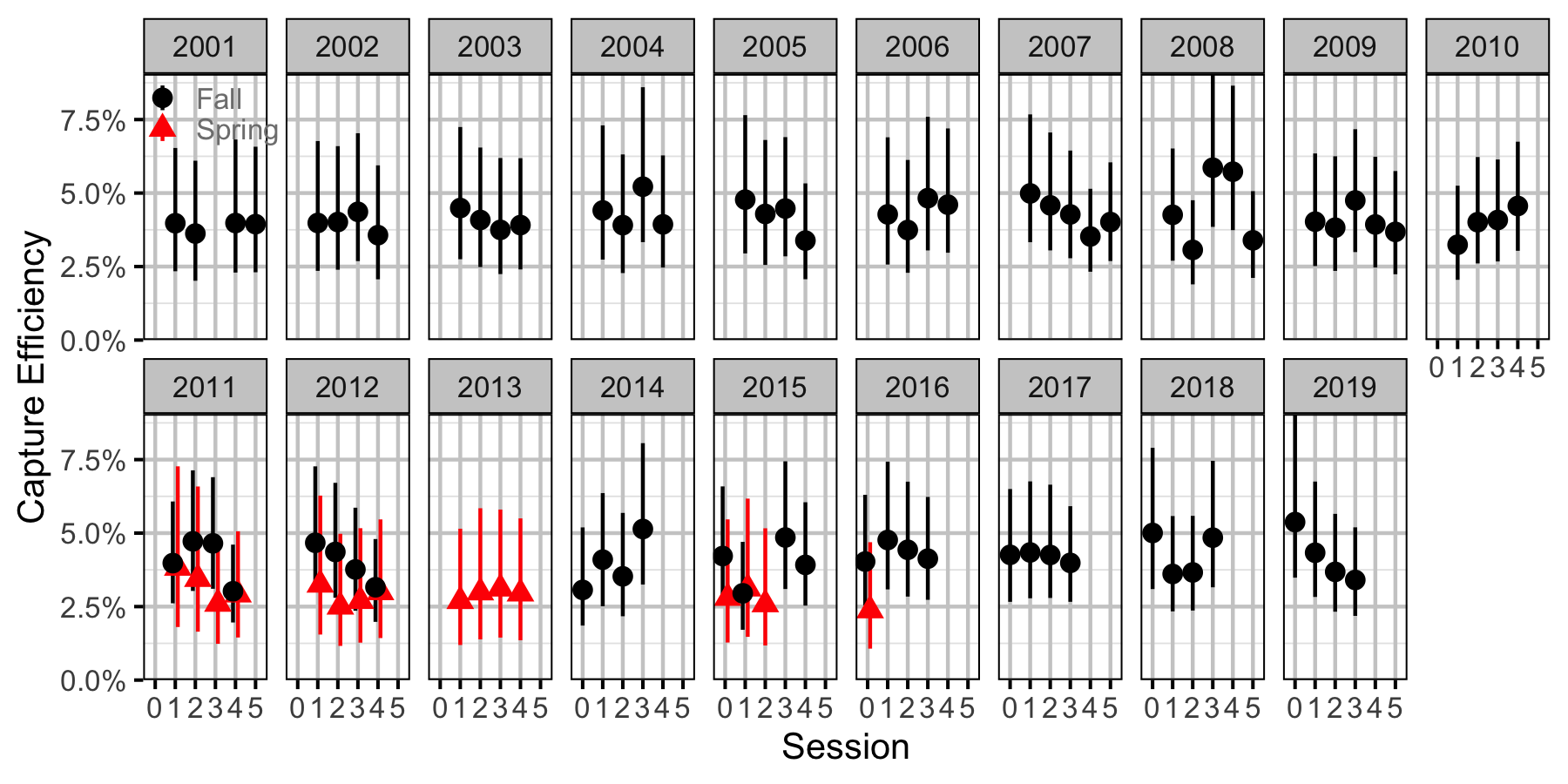
Figure 52. Capture efficiency for Juvenile Bull Trout by session and year (with 95% CIs).
Adult
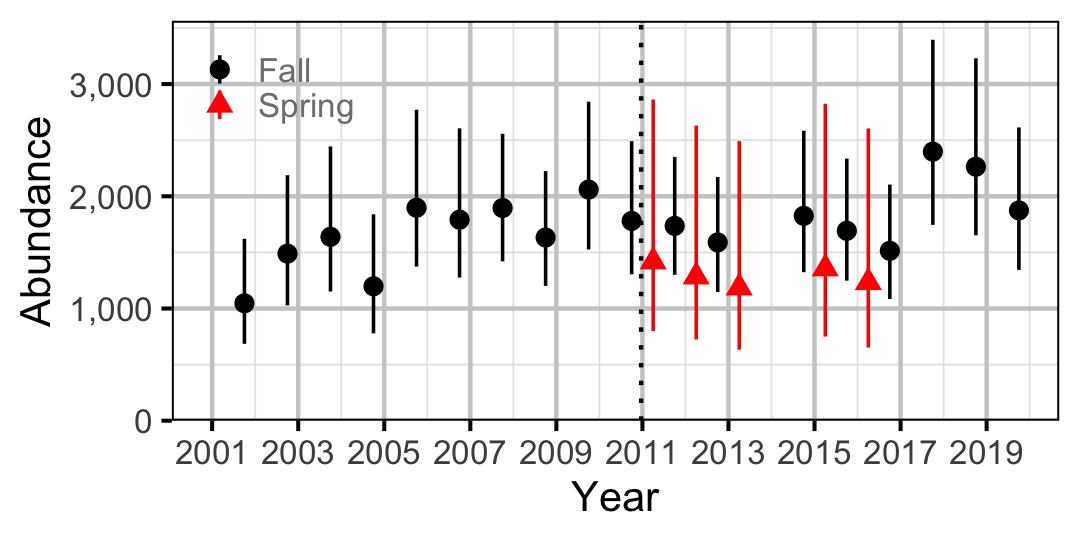
Figure 53. Abundance of Adult Bull Trout by year (with 95% CIs).
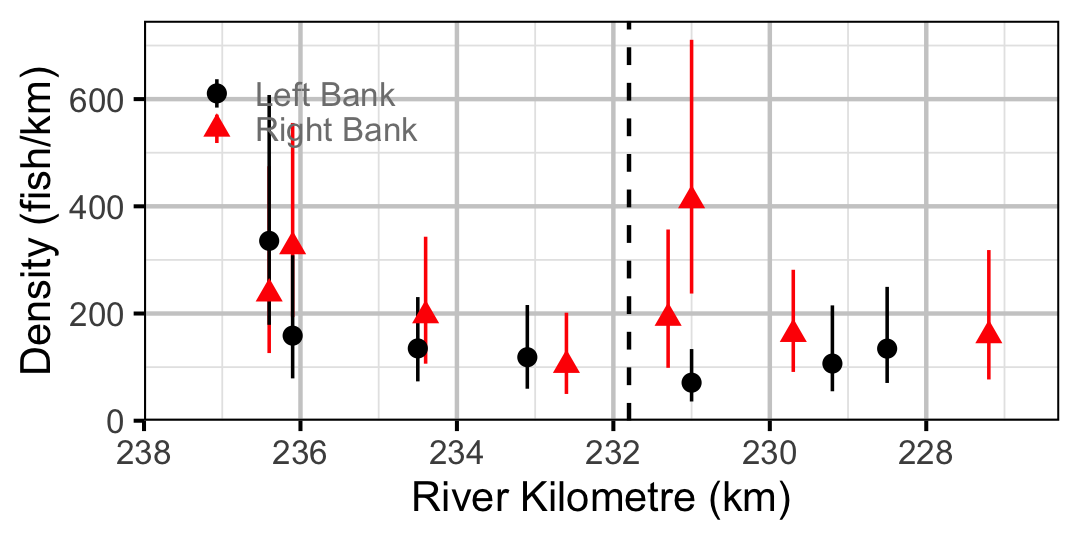
Figure 54. Estimated lineal river count density of Adult Bull Trout by site in 2010(with 95% CIs).
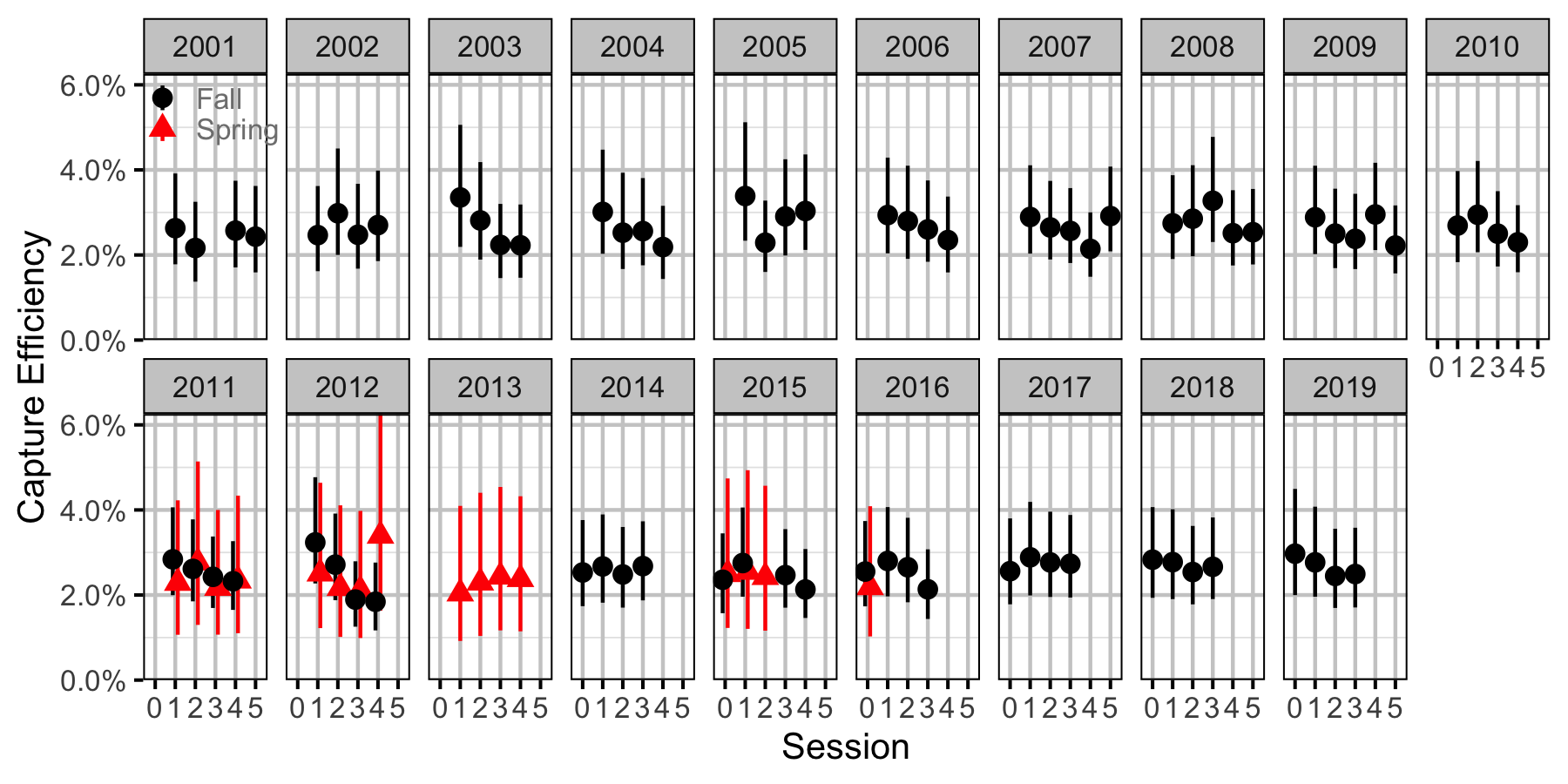
Figure 55. Capture efficiency for Adult Bull Trout by session and year (with 95% CIs).
Mountain Whitefish
Juvenile
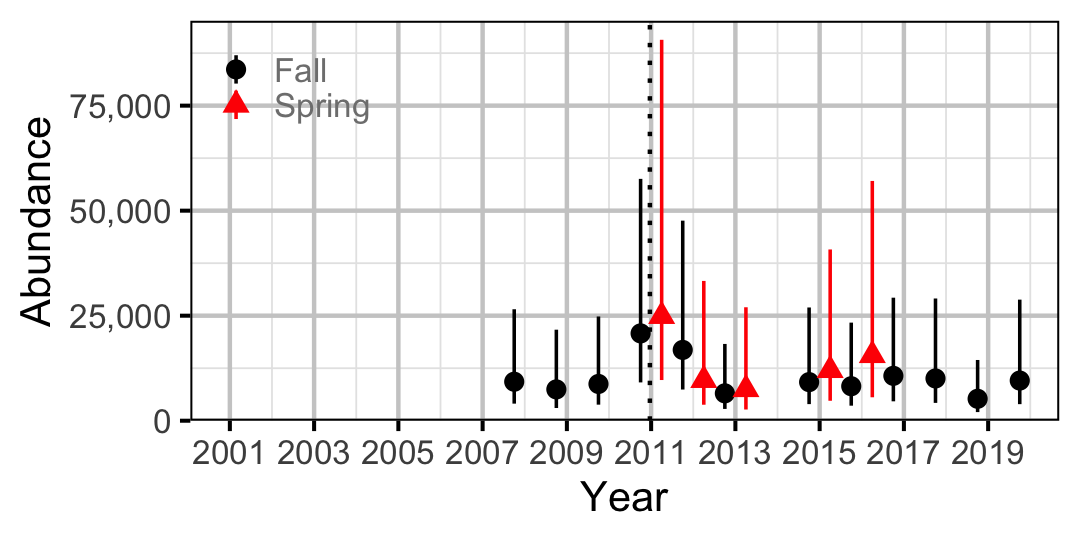
Figure 56. Abundance of Juvenile Mountain Whitefish by year (with 95% CIs).
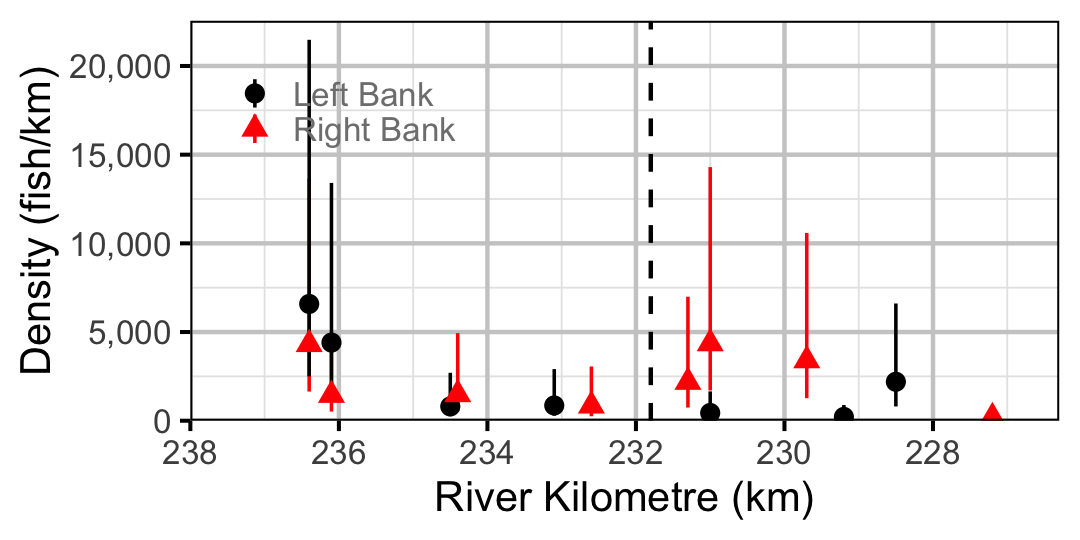
Figure 57. Estimated lineal river count density of Juvenile Mountain Whitefish by site in 2010(with 95% CIs).
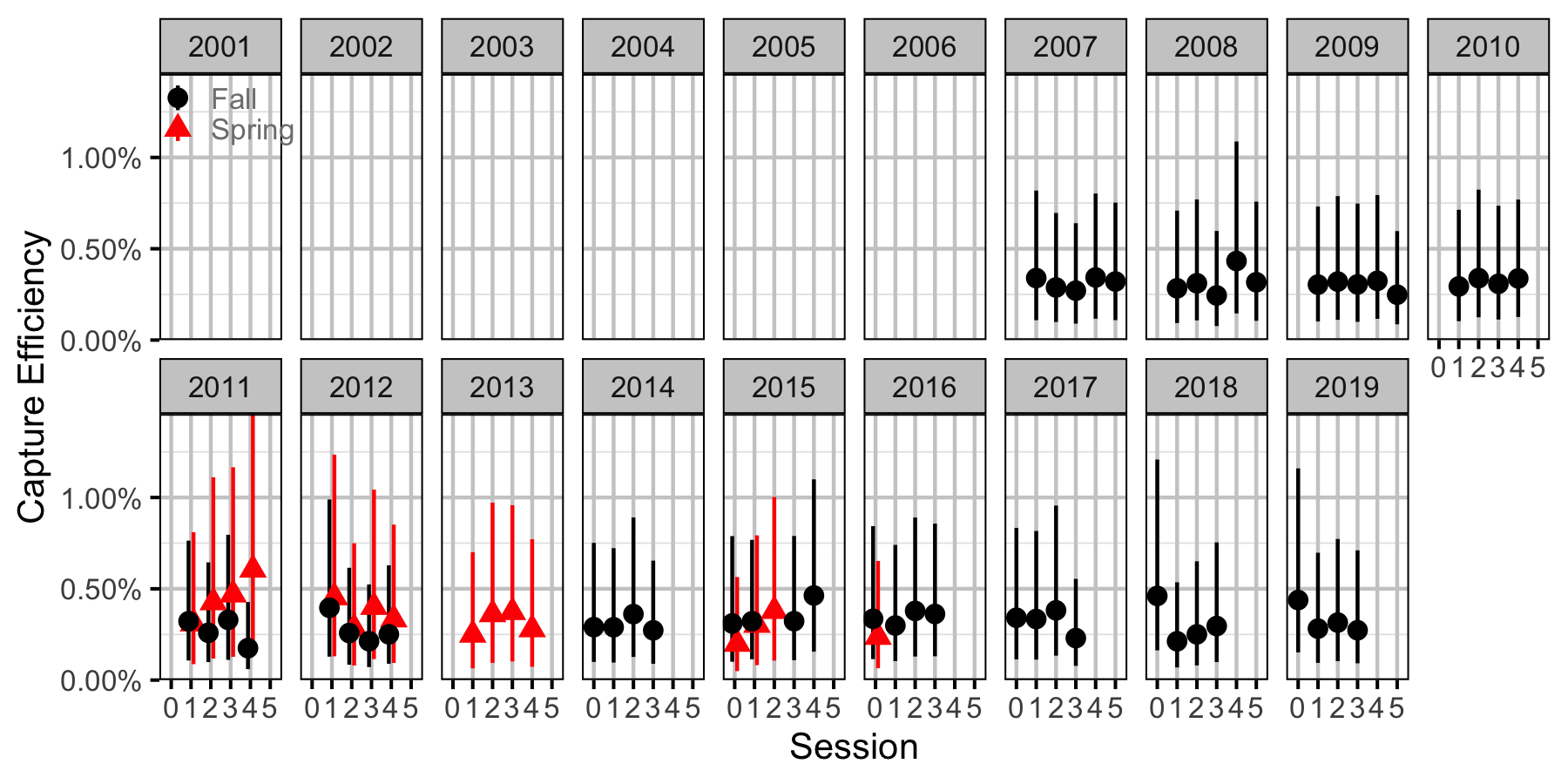
Figure 58. Capture efficiency for Juvenile Mountain Whitefish by session and year (with 95% CIs).
Adult
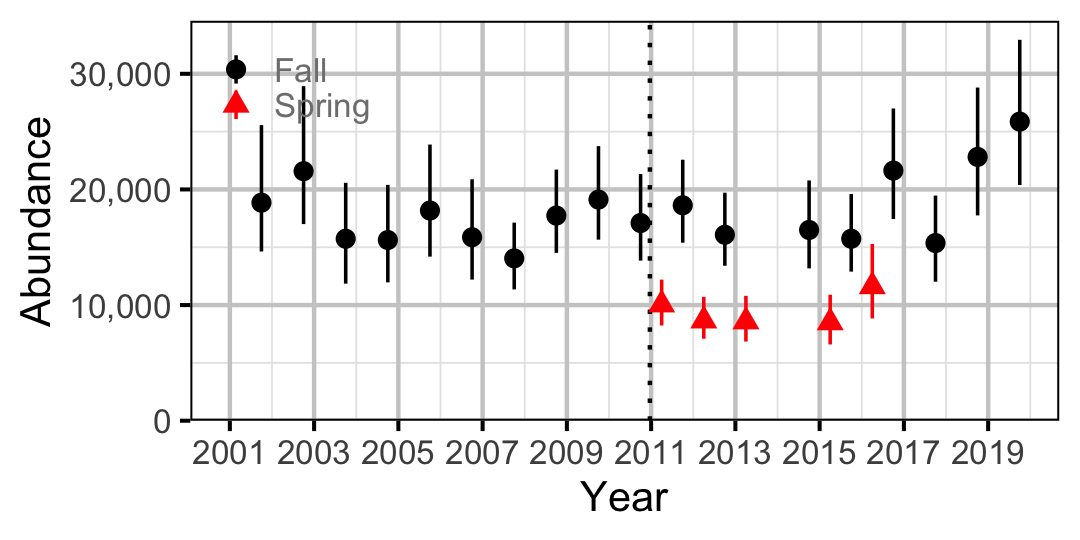
Figure 59. Abundance of Adult Mountain Whitefish by year (with 95% CIs).
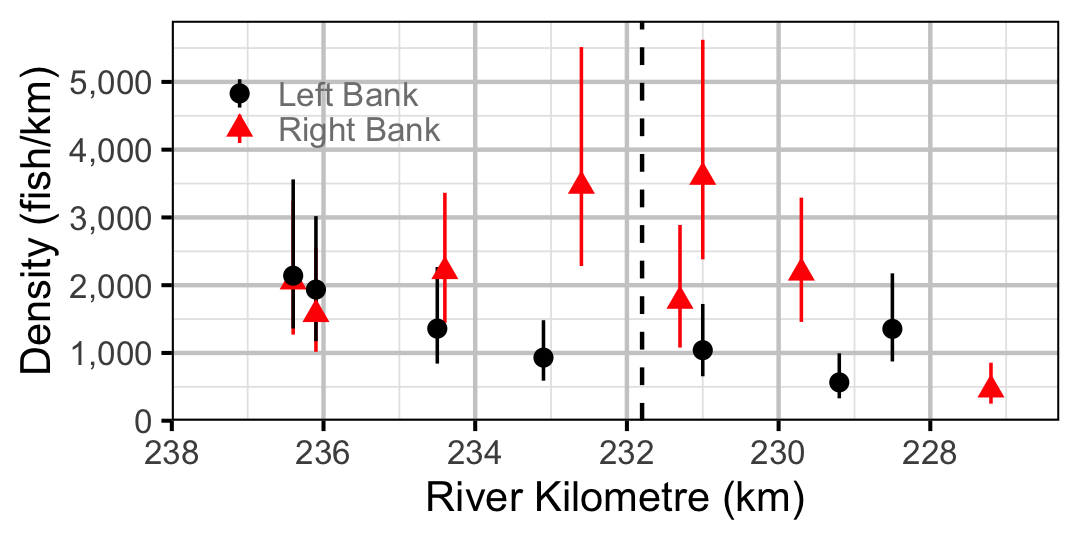
Figure 60. Estimated lineal river count density of Adult Mountain Whitefish by site in 2010(with 95% CIs).
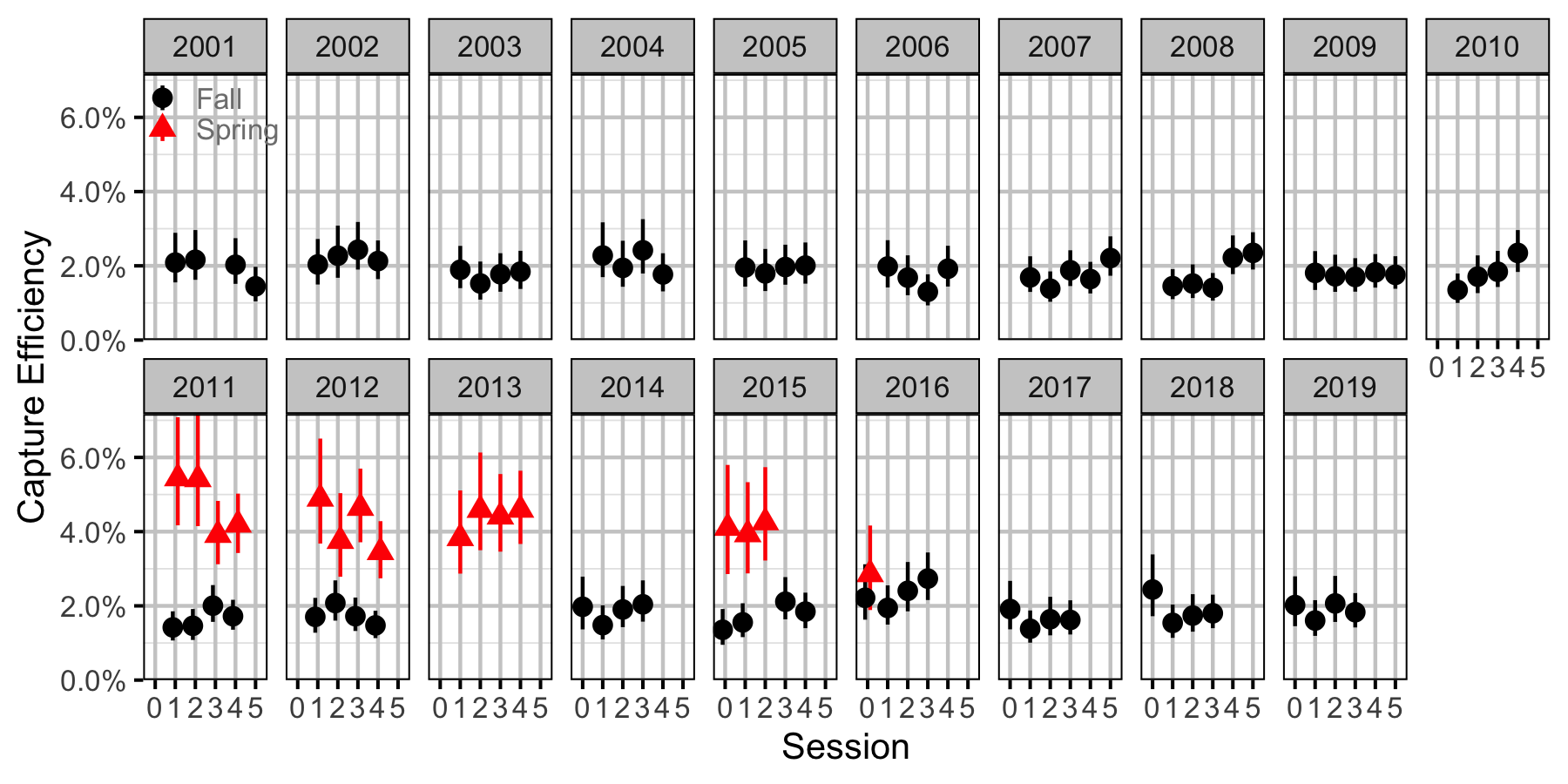
Figure 61. Capture efficiency for Adult Mountain Whitefish by session and year (with 95% CIs).
Rainbow Trout
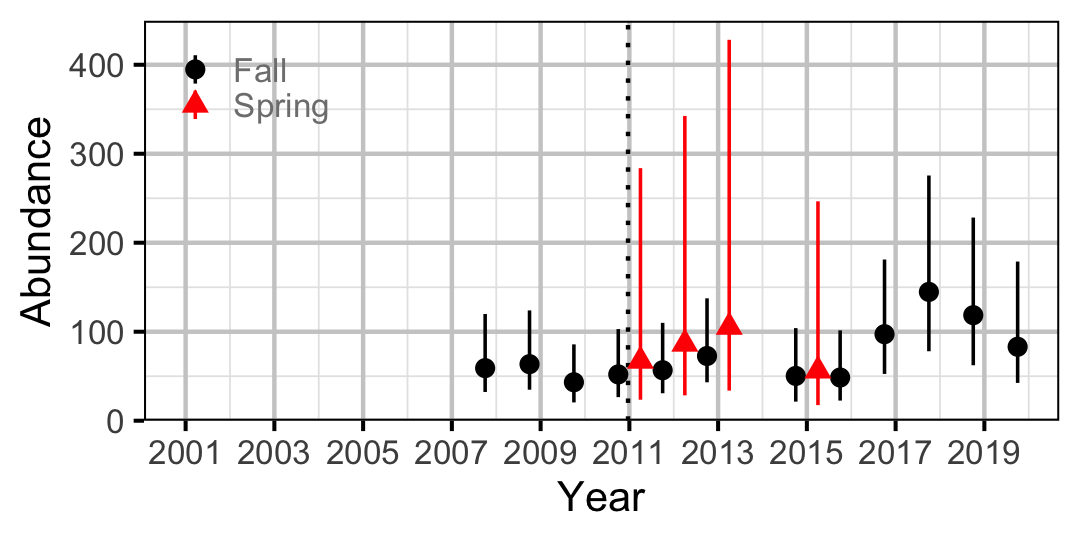
Figure 62. Abundance of Adult Rainbow Trout by year (with 95% CIs).
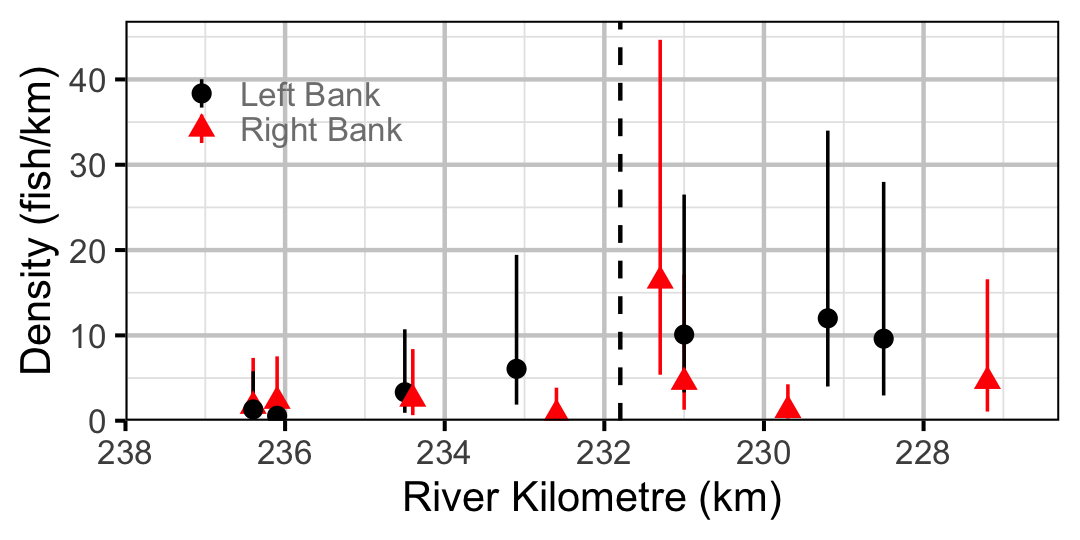
Figure 63. Estimated lineal river count density of Adult Rainbow Trout by site in 2010(with 95% CIs).
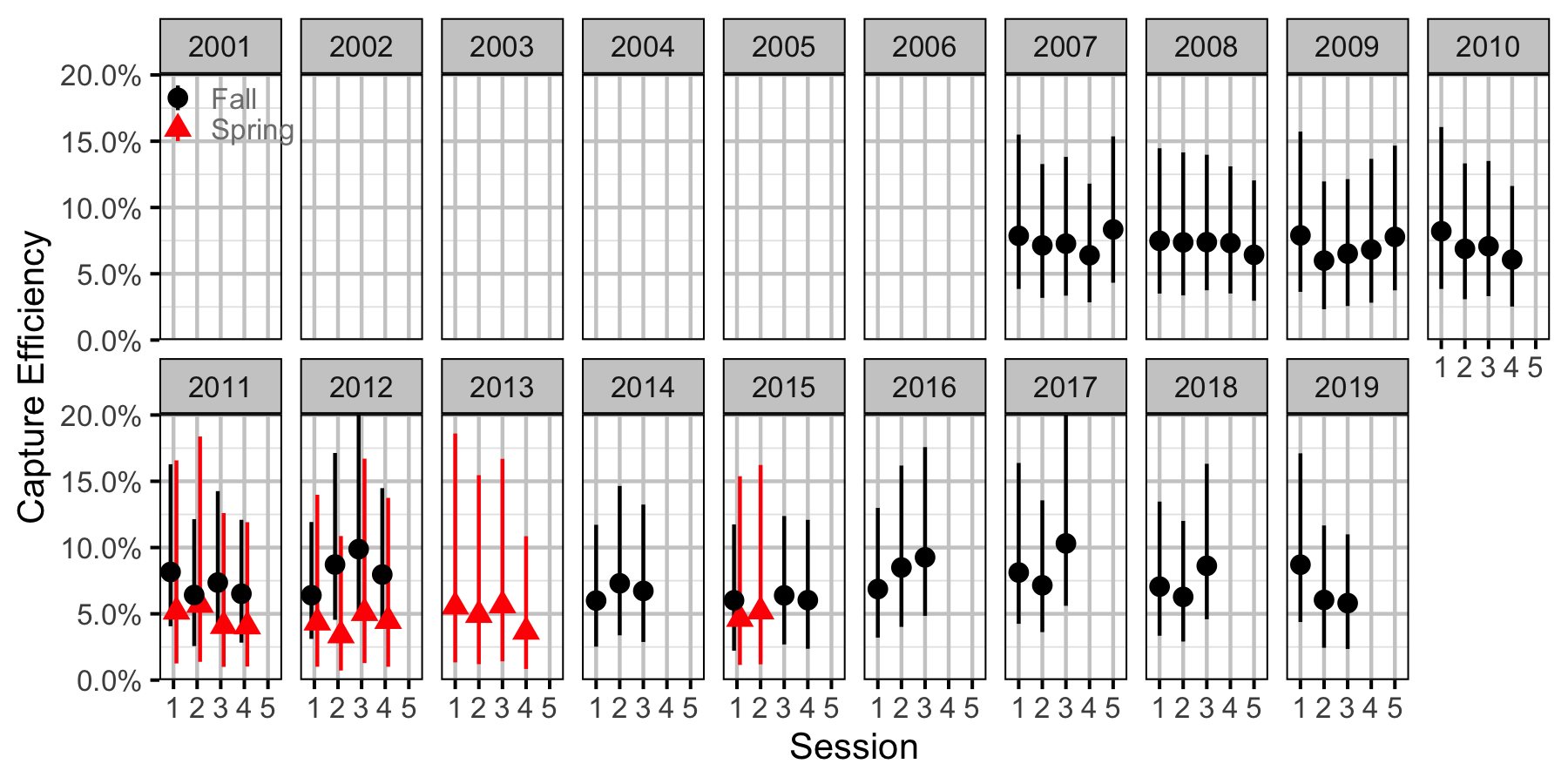
Figure 64. Capture efficiency for Adult Rainbow Trout by session and year (with 95% CIs).
Largescale Sucker
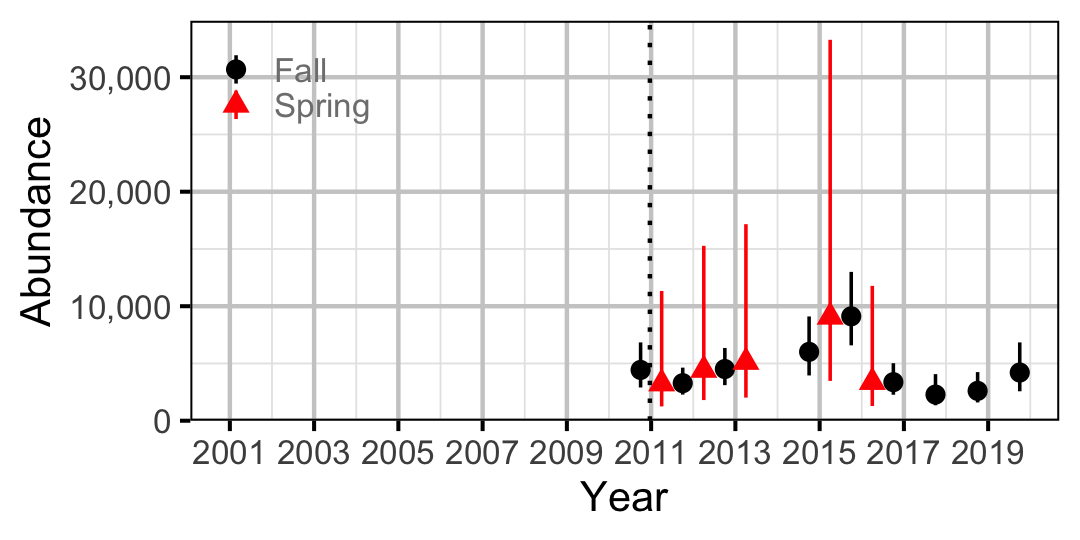
Figure 65. Abundance of Adult Largescale Sucker by year (with 95% CIs).
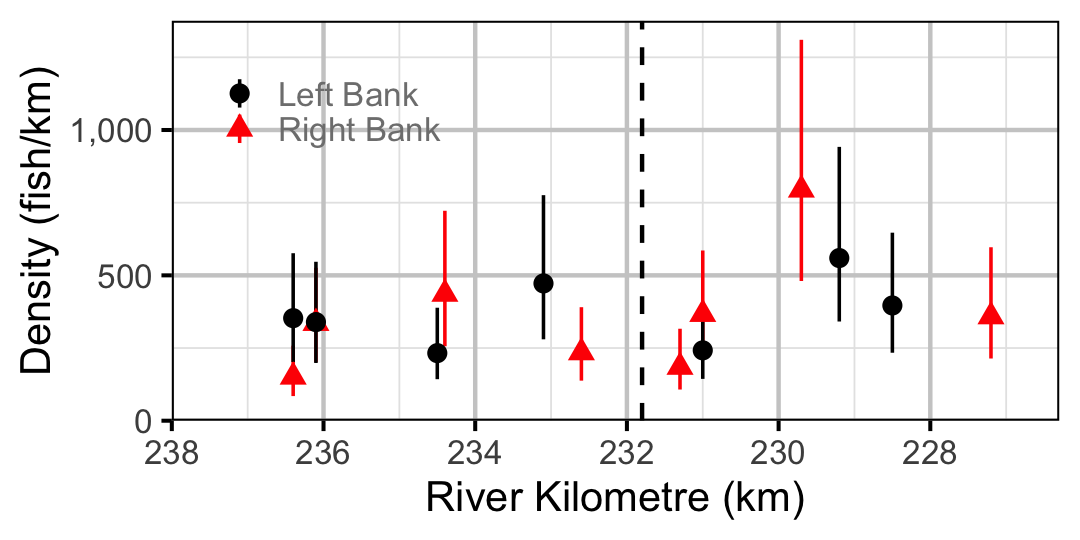
Figure 66. Estimated lineal river count density of Adult Largescale Sucker by site in 2010(with 95% CIs).
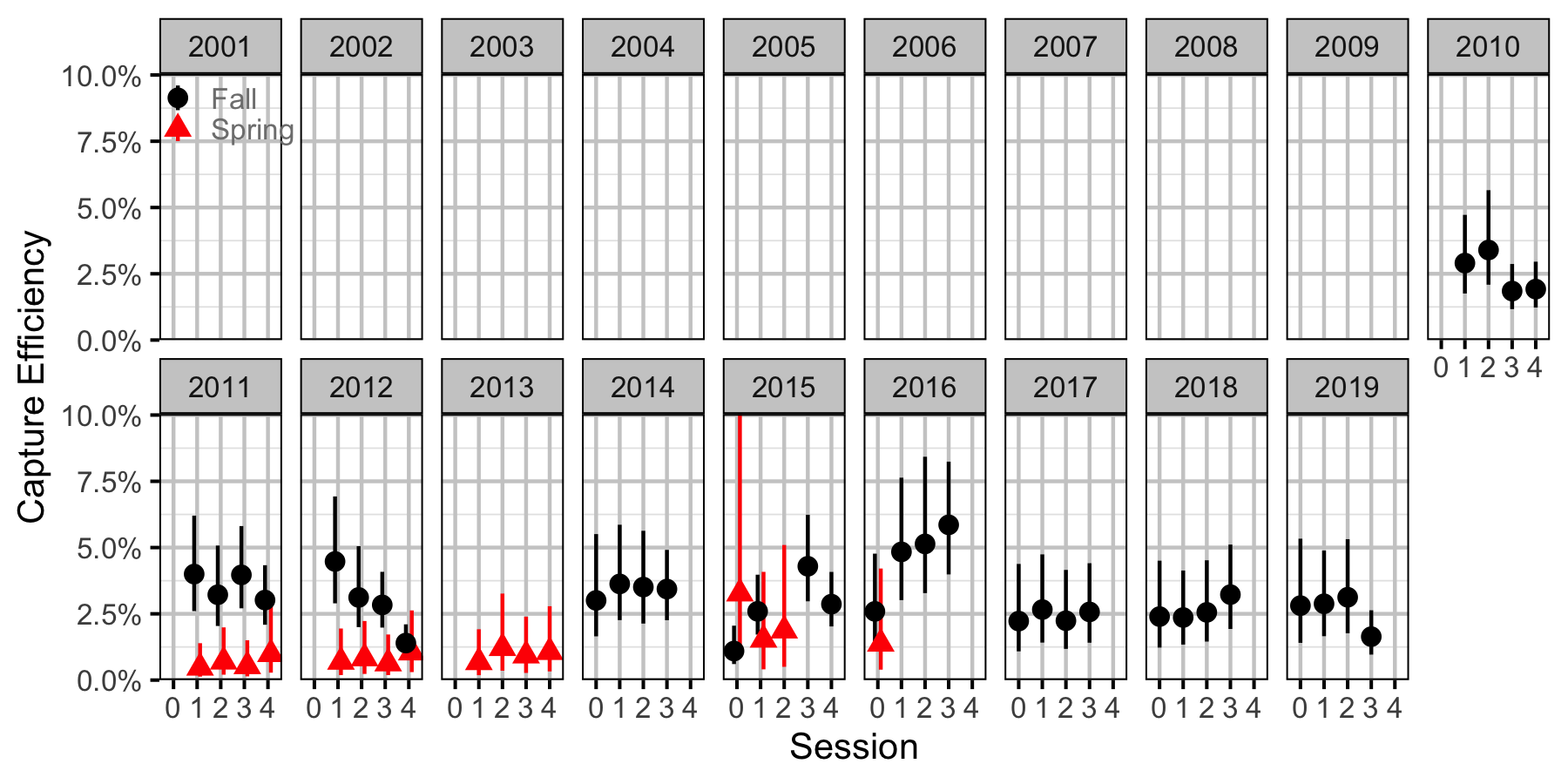
Figure 67. Capture efficiency for Adult Largescale Sucker by session and year (with 95% CIs).
Distribution
Bull Trout
Juvenile
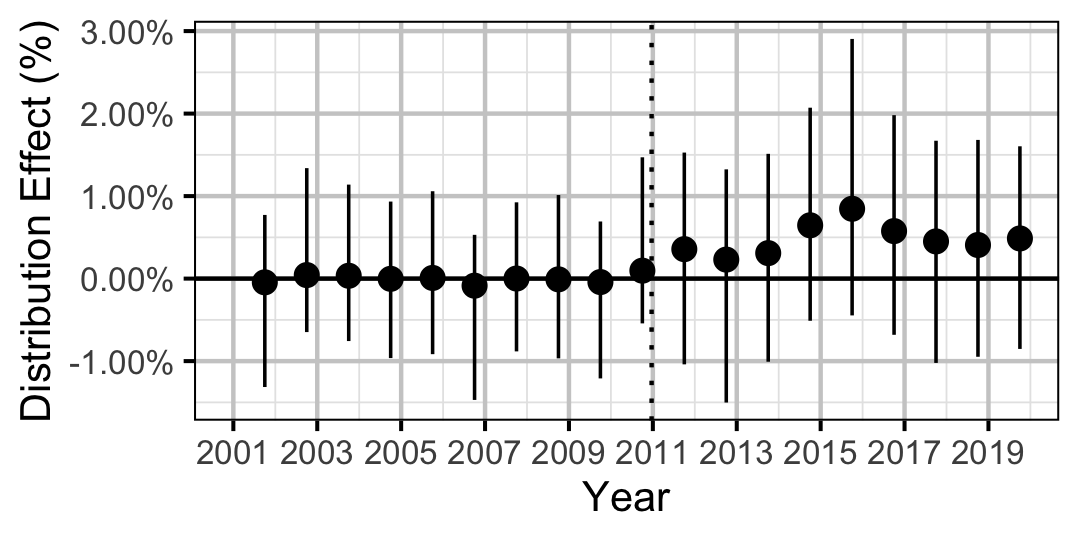
Figure 68. The percent change in the relative upstream density per km (with 95% CIs).
Adult
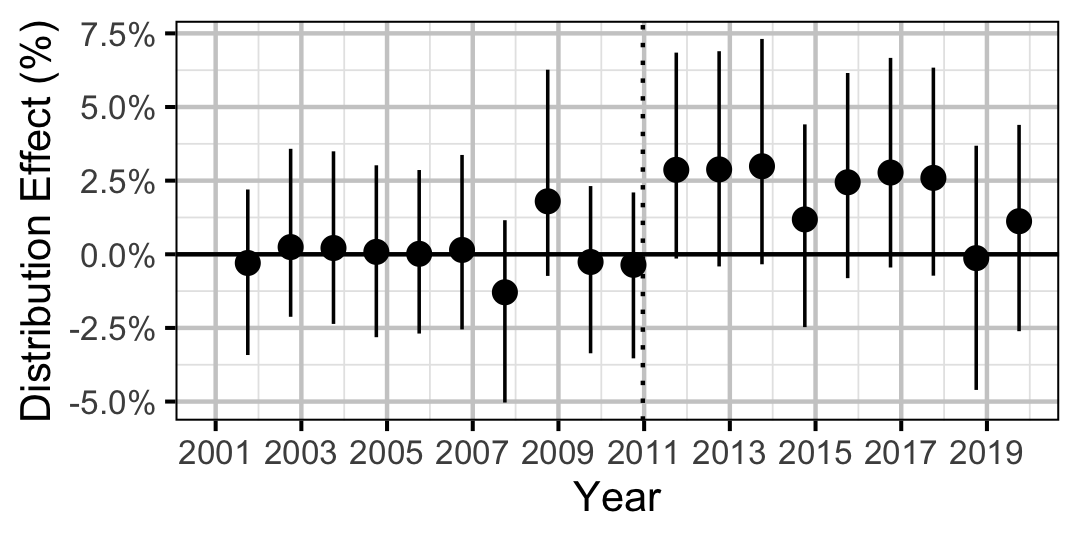
Figure 69. The percent change in the relative upstream density per km (with 95% CIs).
Mountain Whitefish
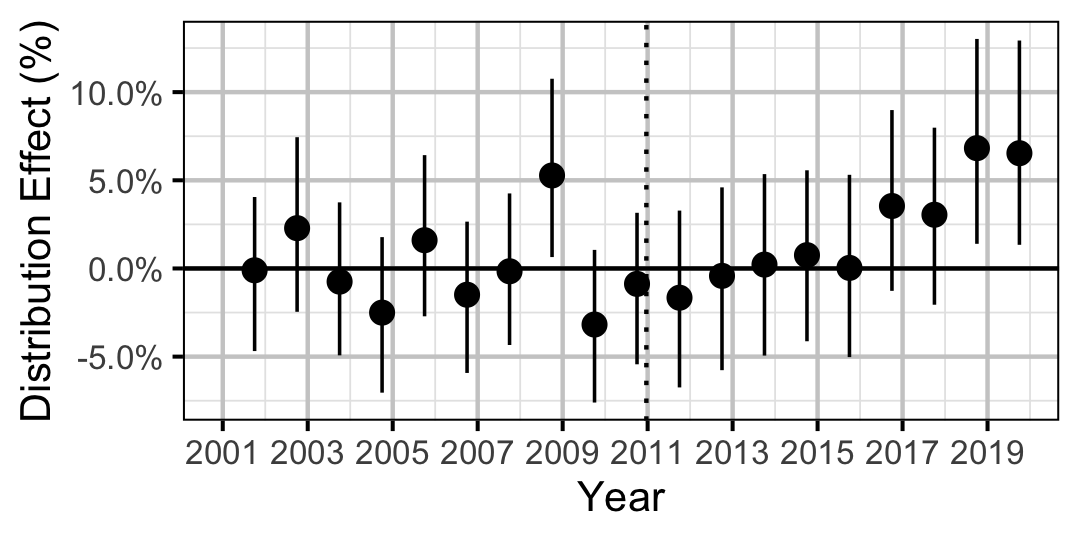
Figure 70. The percent change in the relative upstream density per km (with 95% CIs).
Rainbow Trout
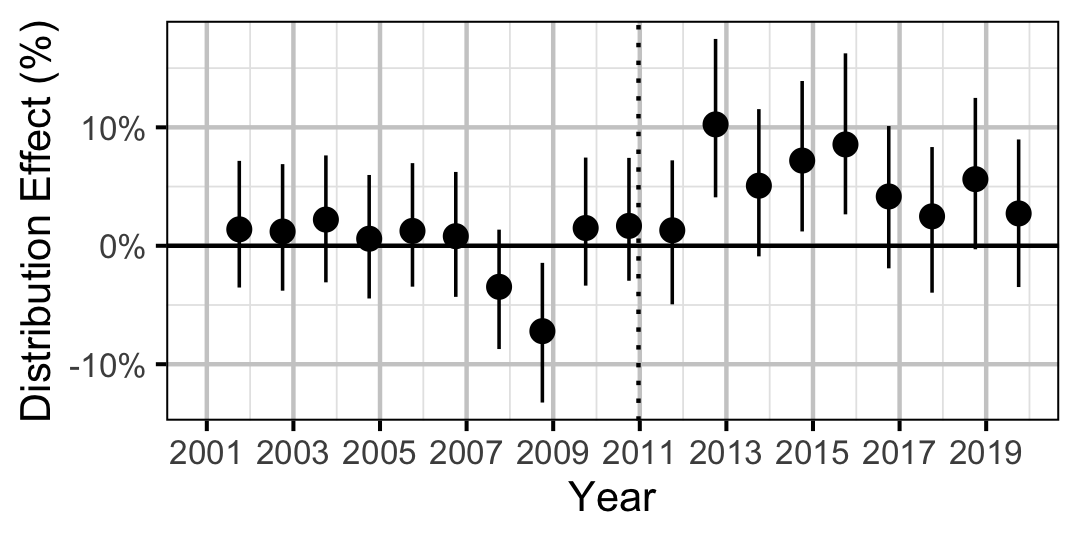
Figure 71. The percent change in the relative upstream density per km (with 95% CIs).
Burbot
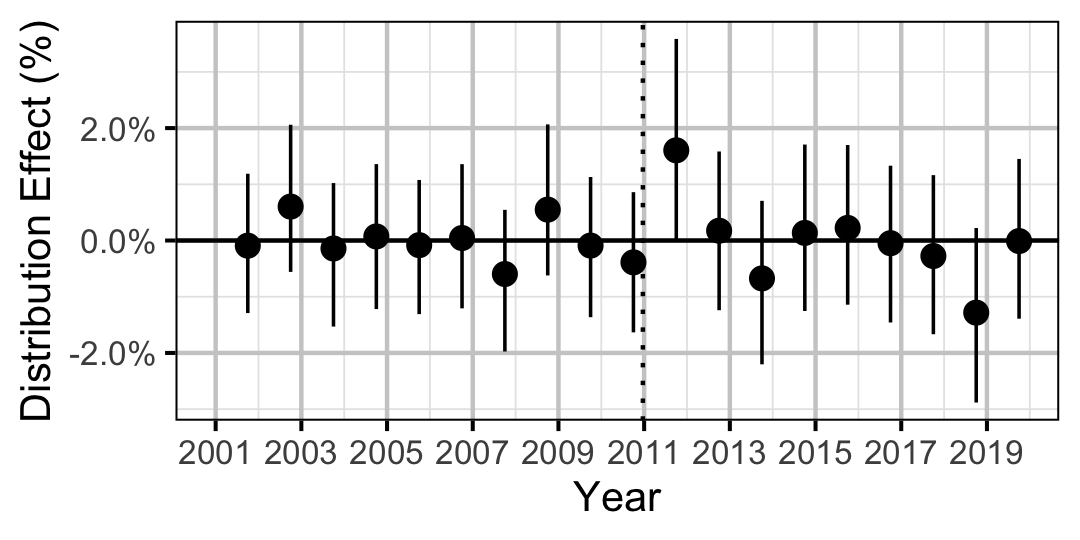
Figure 72. The percent change in the relative upstream density per km (with 95% CIs).
Northern Pikeminnow
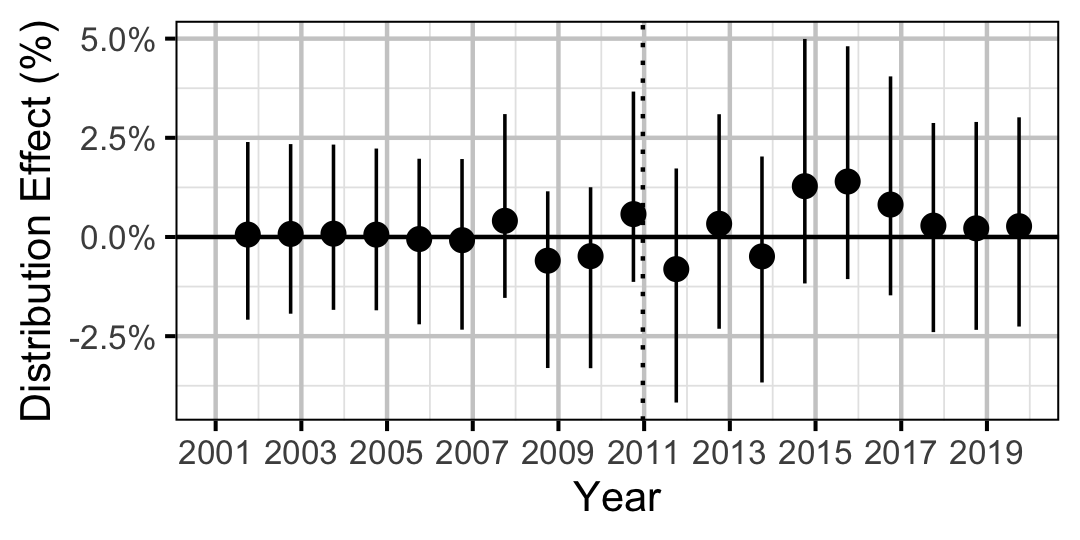
Figure 73. The percent change in the relative upstream density per km (with 95% CIs).
Suckers
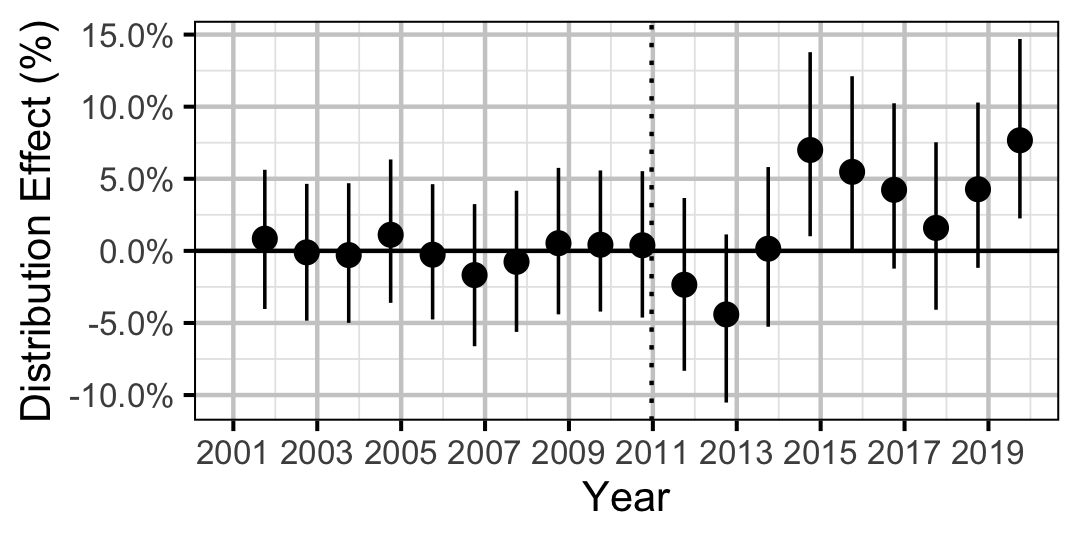
Figure 74. The percent change in the relative upstream density per km (with 95% CIs).
Species Richness
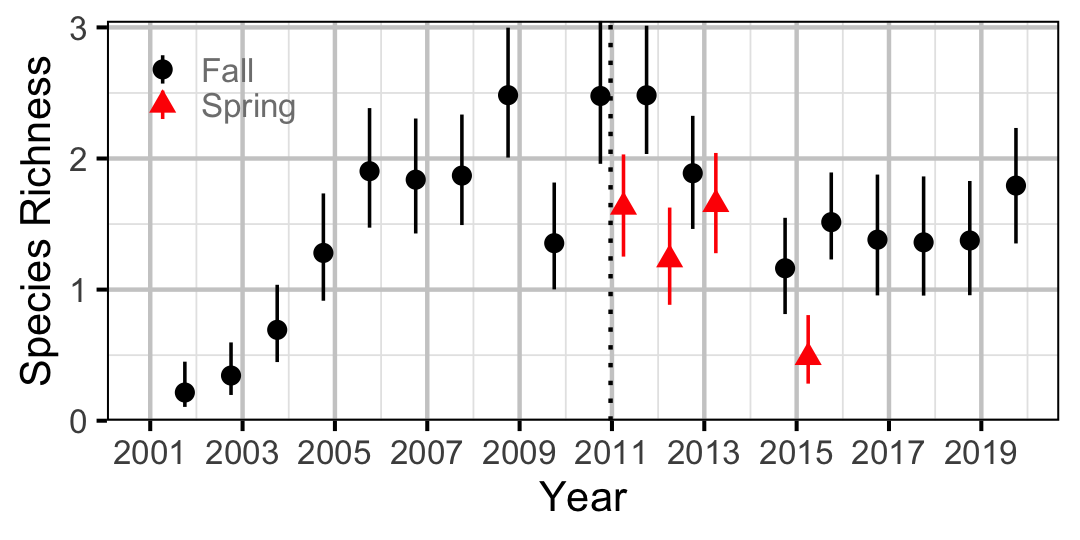
Figure 75. Estimated species richness at a typical site by year (with 95% CIs).
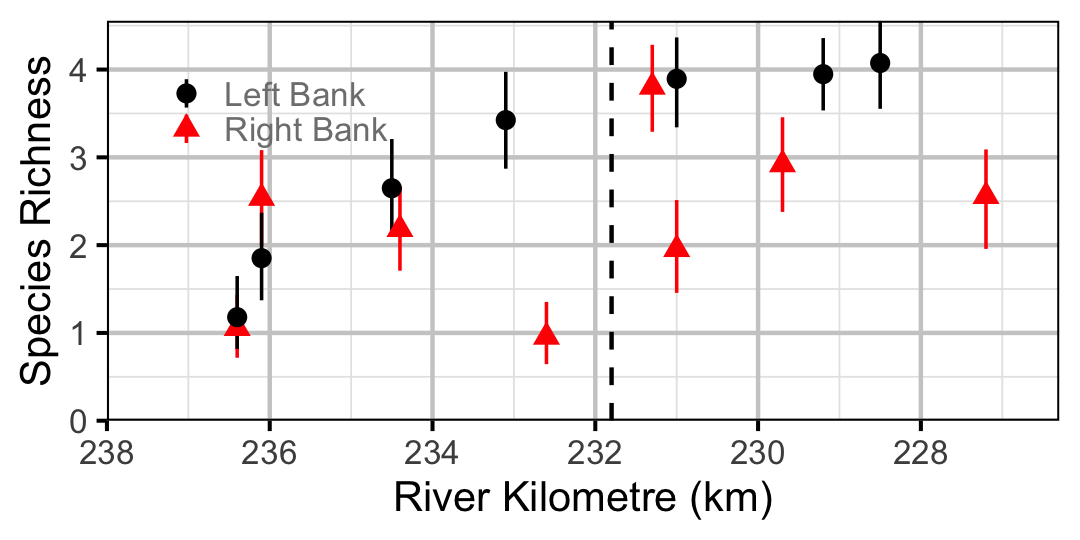
Figure 76. Estimated species richness in 2010 by year (with 95% CIs).
Species Evenness
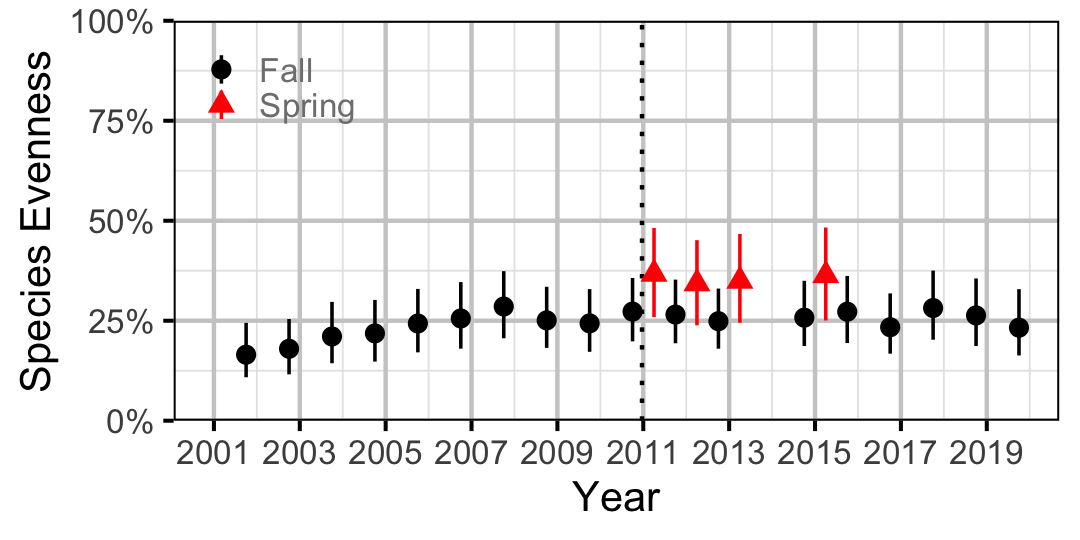
Figure 77. Estimated species evenness by year (with 95% CIs).
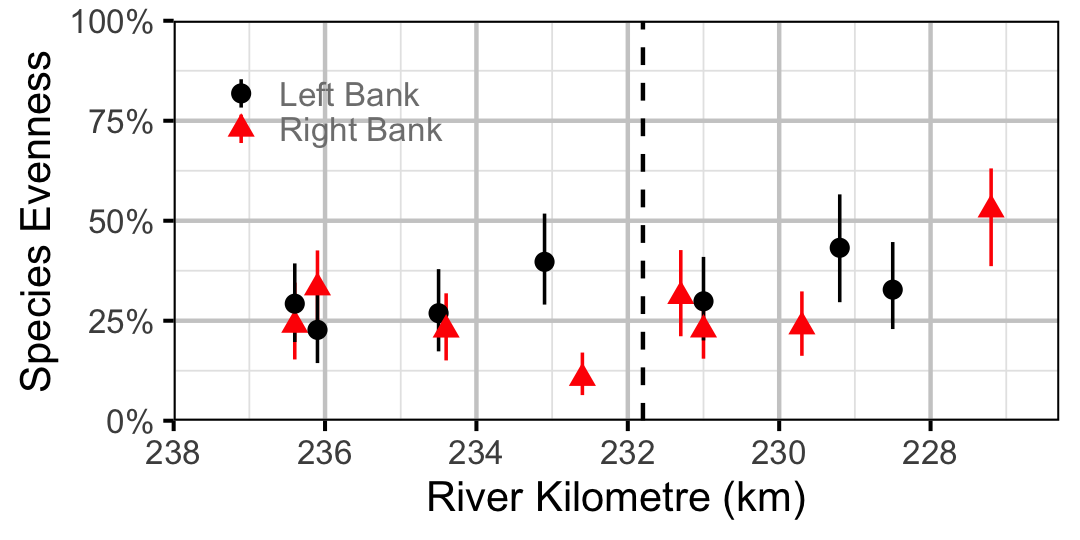
Figure 78. Estimated species evenness by site (with 95% CIs).
Species Diversity
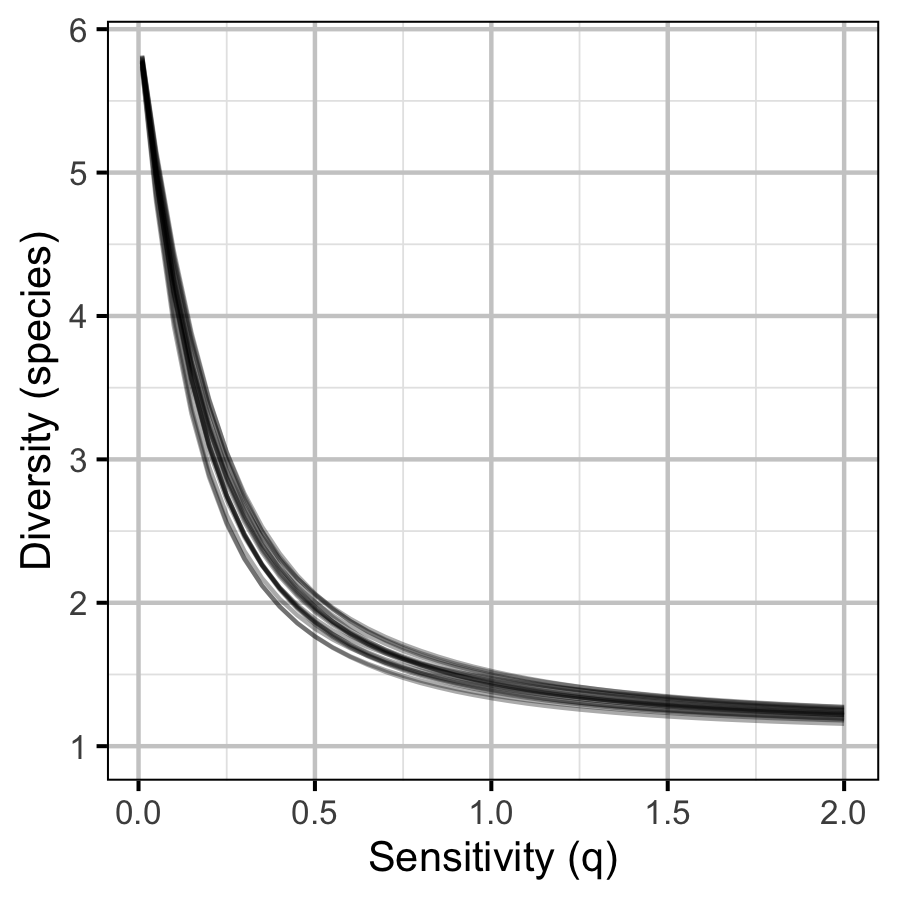
Figure 79. Annual diversity profiles of the effective number of species by the sensitivity parameter.
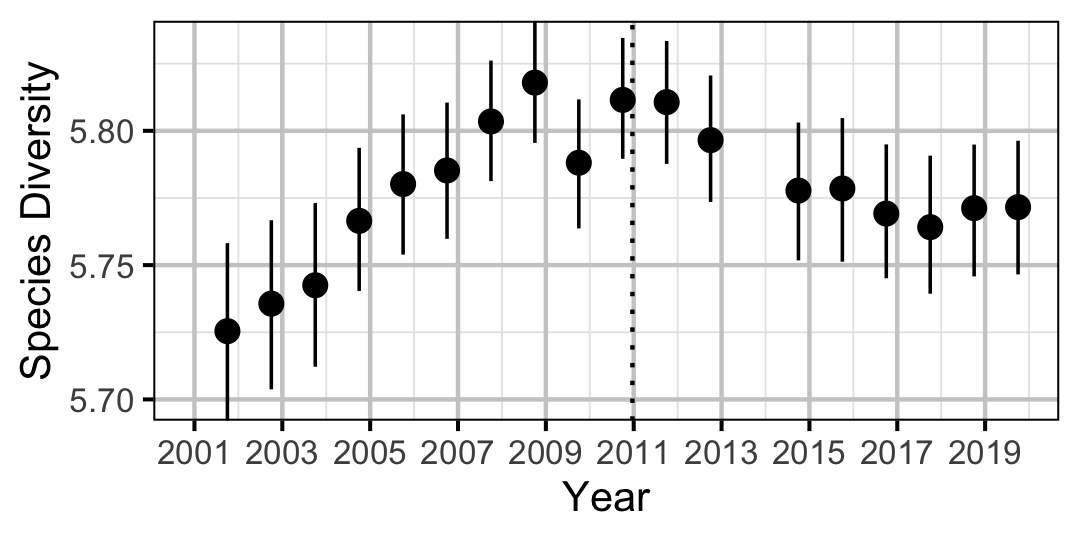
Figure 80. Effective number of species when q = 0.01 by year (with 95% CIs).
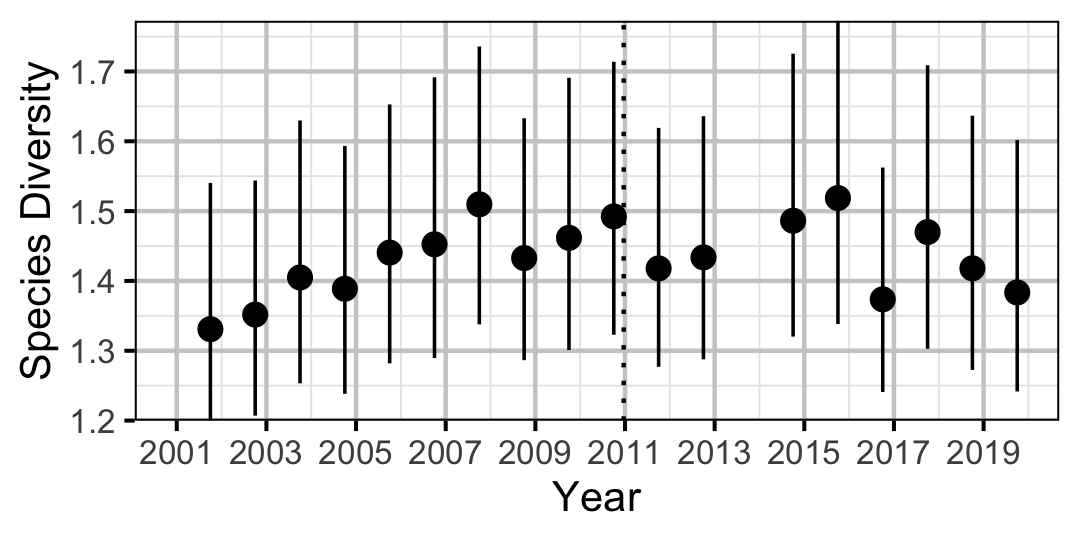
Figure 81. Effective number of species when q = 1.01 by year (with 95% CIs).
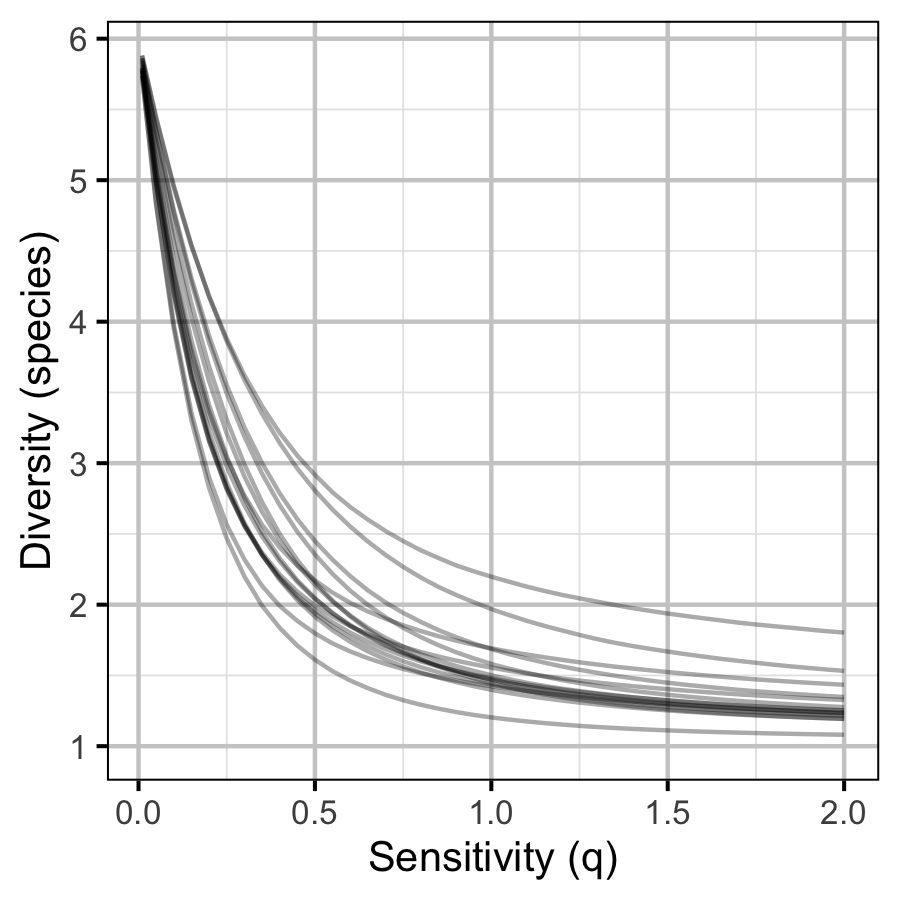
Figure 82. Site diversity profiles of the effective number of species by the sensitivity parameter.
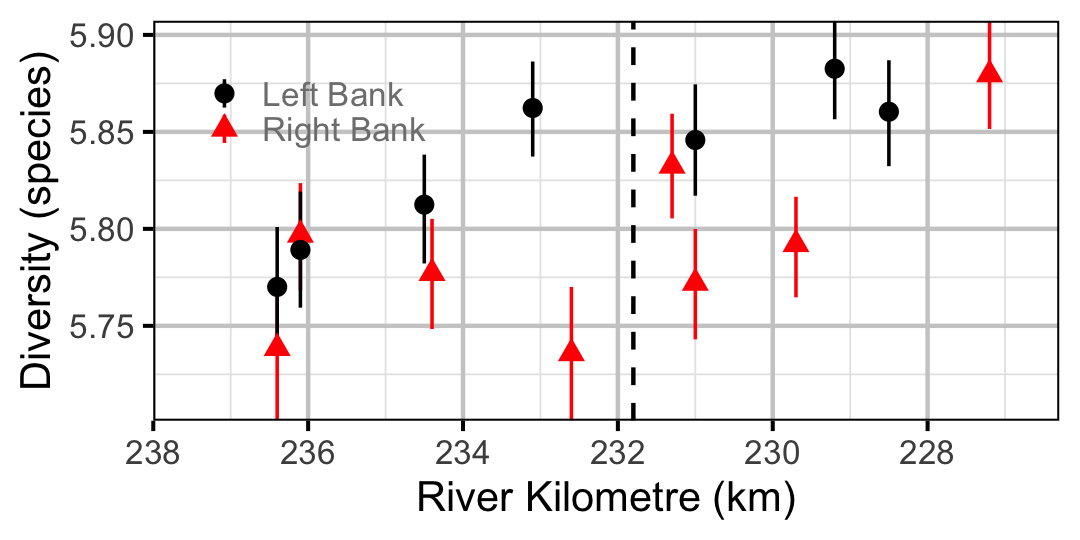
Figure 83. Effective number of species when q = 0.01 by site (with 95% CIs).
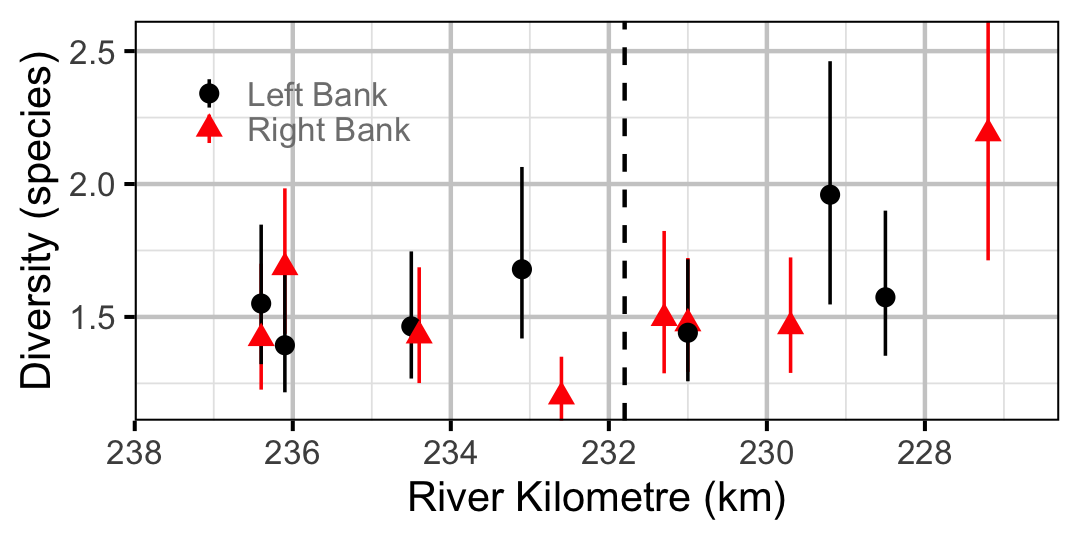
Figure 84. Effective number of species when q = 1.01 by site (with 95% CIs).
Effect Size
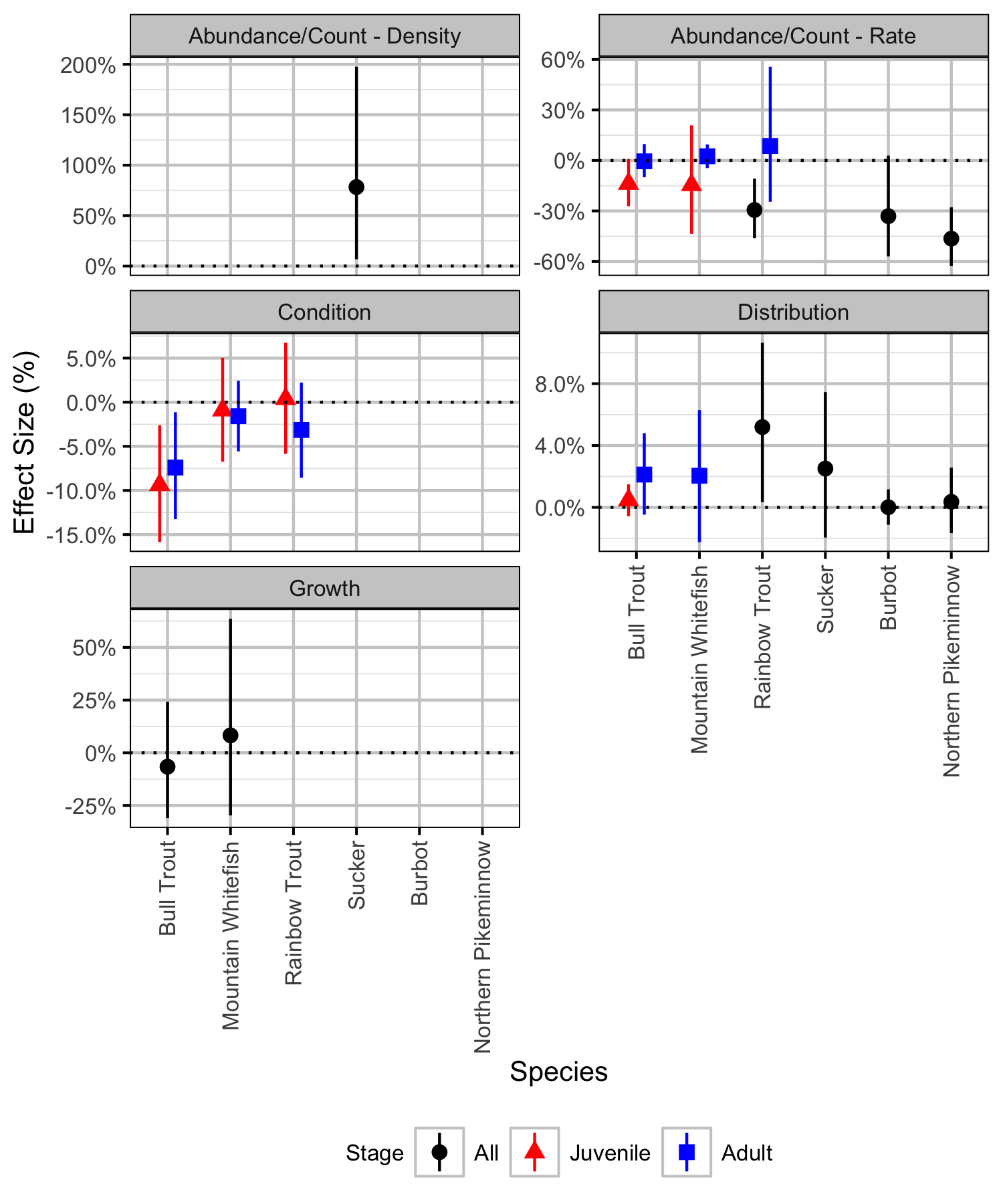
Figure 85. The estimates (with 95% CIs) of the effect of the regime shift by species, analysis and stage. The abundance estimates are the percent change in the annual population growth rate. The distribution estimates are the percent change in the relative upstream density per km.
Acknowledgements
The organisations and individuals whose contributions have made this analysis report possible include:
- BC Hydro
- Guy Martel
- Karen Bray
- Jason Watson
- Okanagan National Alliance
- Dave DeRosa
- Amy Duncan
- Michael Zimmer
- Charlotte Whitney
- Golder Associates
- David Roscoe
- Dustin Ford
- Sima Usvyatsov
- Dana Schmidt
- Poisson Consulting
- Evan Amies-Galonski
- Bronwen Lewis