Middle Columbia River Fish Indexing Analysis 2016
The suggested citation for this analytic report is:
Thorley, J.L. and Campos M. (2017) Middle Columbia River Fish Indexing Analysis 2016. A Poisson Consulting Analysis Report. URL: https://www.poissonconsulting.ca/f/577548349.
Background
The key management questions to be addressed by the analyses are:
- Is there a change in abundance of adult life stages of fish using the Middle Columbia River (MCR) that corresponds with the implementation of a year-round minimum flow?
- Is there a change in growth rate of adult life stages of the most common fish species using the MCR that corresponds with the implementation of a year-round minimum flow?
- Is there a change in body condition (measured as a function of relative weight to length) of adult life stages of fish using the MCR that corresponds with the implementation of a year-round minimum flow?
- Is there a change in spatial distribution of adult life stages of fish using the MCR that corresponds with the implementation of a year-round minimum flow?
Other objectives include the estimation of species richness, species diversity (evenness) and the modeling of environmental-fish metric relationships and scale age data. The year-round minimum flow was implemented in the winter of 2010 at the same time that a fifth turbine was added.
Methods
Data Preparation
The data were provided by Golder Associates.
Life-Stage
The four primary fish species were categorized as fry, juvenile or adult based on their lengths.
Table 1. Length cutoffs by species and stage.
| Species | Fry | Juvenile |
|---|---|---|
| Bull Trout | <120 | <400 |
| Mountain Whitefish | <120 | <175 |
| Rainbow Trout | <120 | <250 |
| Largescale Sucker | <120 | <350 |
Statistical Analysis
Model parameters were estimated using Bayesian methods. The estimates were produced using JAGS (Plummer 2015). For additional information on Bayesian modelling in the BUGS language, of which JAGS uses a dialect, the reader is referred to Kery and Schaub (2011).
Unless indicated otherwise, the Bayesian analyses used uninformative normal prior distributions (Kery and Schaub 2011, 36). The posterior distributions were estimated from 2,000 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of four chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that \(\hat{R} < 1.1\) (Kery and Schaub 2011, 40) for each of the monitored parameters (Kery and Schaub 2011, 61).
The parameters are summarised in terms of the point estimate, standard deviation (sd), the z-score, lower and upper 95% confidence/credible limits (CLs) and the p-value (Kery and Schaub 2011, 37, 42). The estimate is the median (50th percentile) of the MCMC samples, the z-score is \(\mathrm{mean}/\mathrm{sd}\) and the 95% CLs are the 2.5th and 97.5th percentiles. A p-value of 0.05 indicates that the lower or upper 95% CL is 0.
Where relevant, model adequacy was confirmed by examination of residual plots for the full model(s).
The results are displayed graphically by plotting the modeled relationships between particular variables and the response(s) with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values, respectively, while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). When informative the influence of particular variables is expressed in terms of the effect size (i.e., percent change in the response variable) with 95% confidence/credible intervals (CIs, Bradford, Korman, and Higgins 2005).
The analyses were implemented using R version 3.3.2
(R Core Team 2016) and the jmbr package.
Growth
Annual growth was estimated from the inter-annual recaptures using the Fabens method (Fabens 1965) for estimating the von Bertalanffy (VB) growth curve (von Bertalanffy 1938). The VB curves is based on the premise that
\[ \frac{dl}{dt} = k (L_{\infty} - l)\]
where \(l\) is the length of the individual, \(k\) is the growth coefficient and \(L_{\infty}\) is the mean maximum length.
Integrating the above equation gives
\[ l_t = L_{\infty} (1 - e^{-k(t - t0)})\]
where \(l_t\) is the length at time \(t\) and \(t0\) is the time at which the individual would have had no length.
The Fabens form allows
\[ l_r = l_c + (L_{\infty} - l_c) (1 - e^{-kT})\]
where \(l_r\) is the length at recapture, \(l_c\) is the length at capture and \(T\) is the time at large.
Key assumptions of the growth model include:
- \(L_{\infty}\) is constant.
- \(k\) can vary with discharge regime.
- \(k\) can vary randomly with year.
- The residual variation in growth is normally distributed.
Condition
Condition was estimated via an analysis of mass-length relations (He et al. 2008).
More specifically the model was based on the allometric relationship
\[ W = \alpha L^{\beta}\]
where \(W\) is the weight (mass), \(\alpha\) is the coefficent, \(\beta\) is the exponent and \(L\) is the length.
To improve chain mixing the relation was log-transformed, i.e.,
\[ \log(W) = \log(\alpha) + \beta \log(L)\]
and the logged lengths centered, i.e., \(\log(L) - \overline{\log(L)}\), prior to model fitting.
Preliminary analyses indicated that the variation in the exponent \(\beta\) with respect to year was not informative.
Key assumptions of the final condition model include:
- The expected weight varies with length as an allometric relationship.
- The intercept of the log-transformed allometric relationship is described by a linear mixed model.
- The intercept of the log-transformed allometric relationship varies with discharge regime and season.
- The intercept of the log-transformed allometric relationship varies randomly with year, site and the interaction between year and site.
- The slope of the log-transformed allometric relationship is described by a linear mixed model.
- The slope of the log-transformed allometric relationship varies with discharge regime and season.
- The slope of the log-transformed allometric relationship varies randomly with year.
- The residual variation in weight for the log-transformed allometric relationship is independently and identically normally distributed.
Occupancy
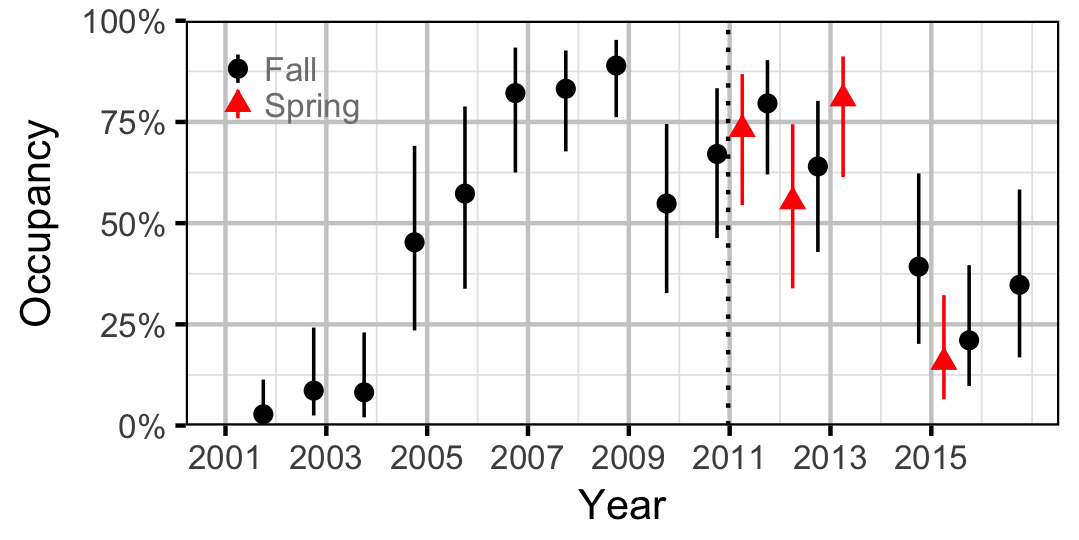
Occupancy, which is the probability that a particular species was present at a site, was estimated from the temporal replication of detection data (Kery, 2010; Kery and Schaub, 2011, pp. 238-242 and 414-418), i.e., each site was surveyed multiple times within a season. A species was considered to have been detected if one or more individuals of the species were caught or counted. It is important to note that the model estimates the probability that the species was present at a given (or typical) site in a given (or typical) year as opposed to the probability that the species was present in the entire study area. We focused on Northern Pikeminnow, Burbot, Lake Whitefish, Rainbow Trout, Redside Shiner and Sculpins because they were low enough density to not to be present at all sites at all times yet were encounted sufficiently often to provide information on spatial and temporal changes.
Key assumptions of the occupancy model include:
- Occupancy (probability of presence) is described by a generalized linear mixed model with a logit link.
- Occupancy varies with season.
- Occupancy varies randomly with site.
- The effect of year on occupancy is autoregressive with a lag of one year and varies with discharge regime.
- Sites are closed, i.e., the species is present or absent at a site for all the sessions in a particular season of a year.
- Observed presence is described by a bernoulli distribution, given occupancy.
Species Richness
The estimated probabilities of presence for the six species considered in the occupany analyses were summed to give the expected species richnesses by site and year.
Count
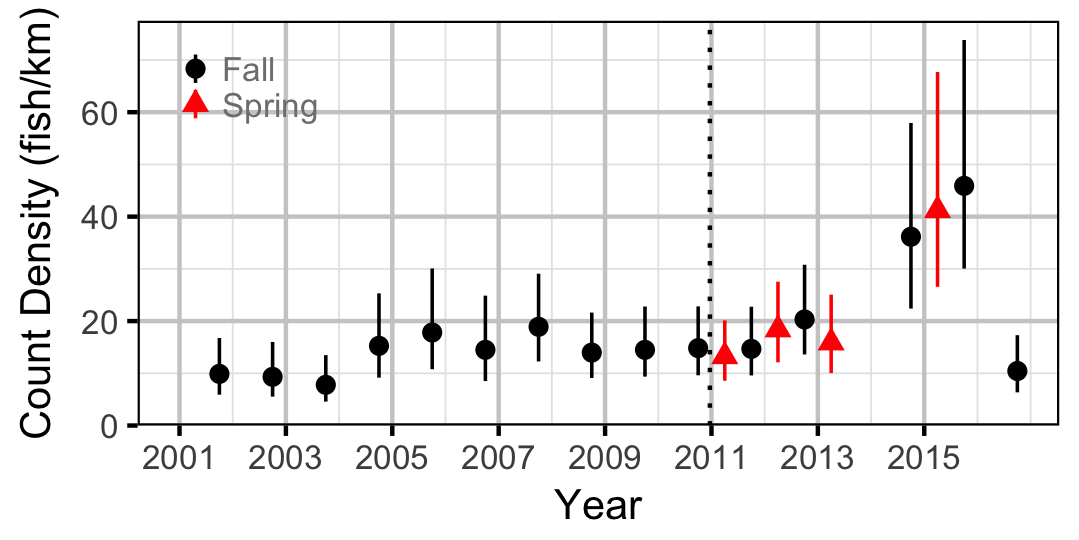
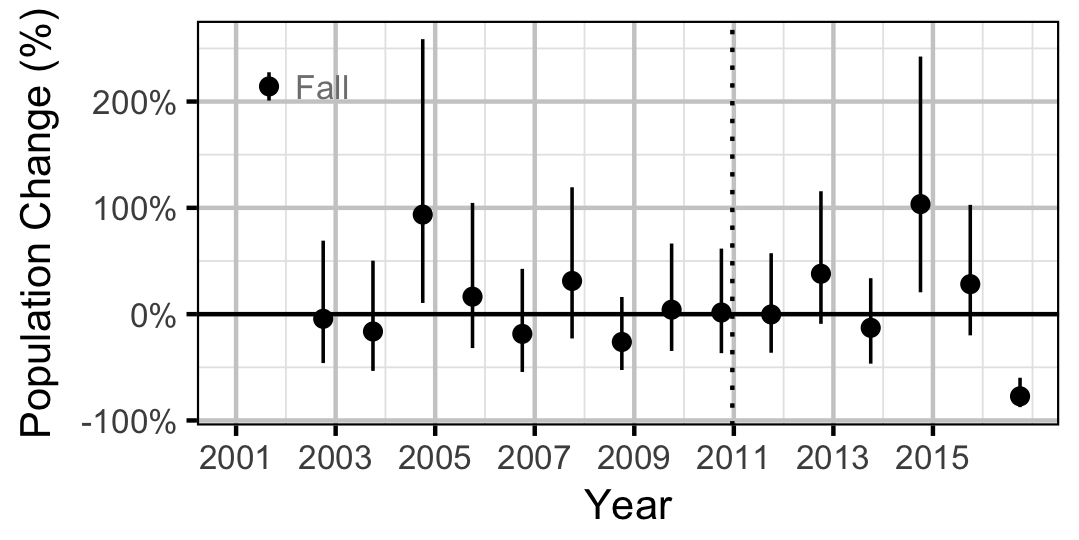
The count data were analysed using an overdispersed Poisson model (Kery, 2010; Kery and Schaub, 2011, pp. 168-170,180 and 55-56) to provide estimates of the lineal river count density (count/km) by year and site. Unlike Kery (2010) and Kery and Schaub (2011), which used a log-normal distribution to account for the extra-Poisson variation, the current model used a gamma distribution with identical shape and scale parameters because it has a mean of 1 and therefore no overall effect on the expected count. The count data does not enable us to estimate abundance nor observer efficiency, but it enables us to estimate an expected count, which is the product of the two. As such it is necessary to assume that changes in observer efficiency are negligible in order to interpret the estimates as relative density.
Key assumptions of the count model include:
- Lineal density (fish/km) is described by an autoregressive generalized linear mixed model with a logarithm link.
- Lineal density (fish/km) varies with season.
- Lineal density (fish/km) varies randomly with year, site and the interaction between site and year.
- The effect of year on lineal density (fish/km) is autoregressive with a lag of one year and varies with discharge regime.
- The counts are gamma-Poisson distributed, given the mean count.
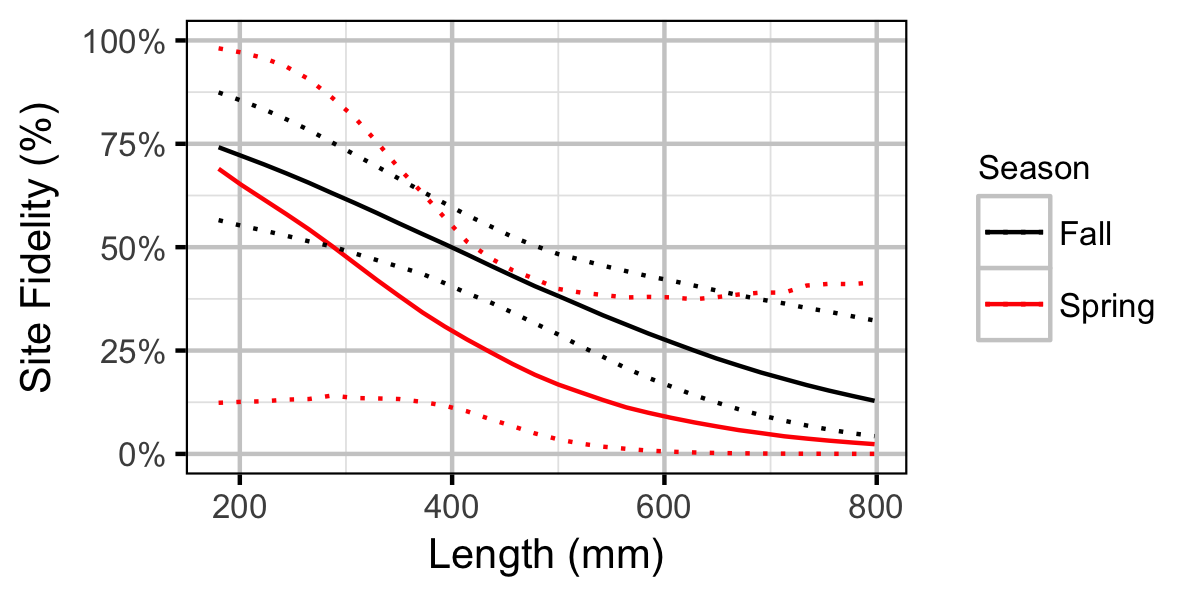
Movement
The extent to which sites are closed, i.e., fish remain at the same site between sessions, was evaluated from a logistic ANCOVA (Kery 2010). The model estimated the probability that intra-annual recaptures were caught at the same site versus a different one.
Key assumptions of the site fidelity model include:
- Site fidelity varies with season, length and the interaction between season and length.
- Observed site fidelity is Bernoulli distributed.
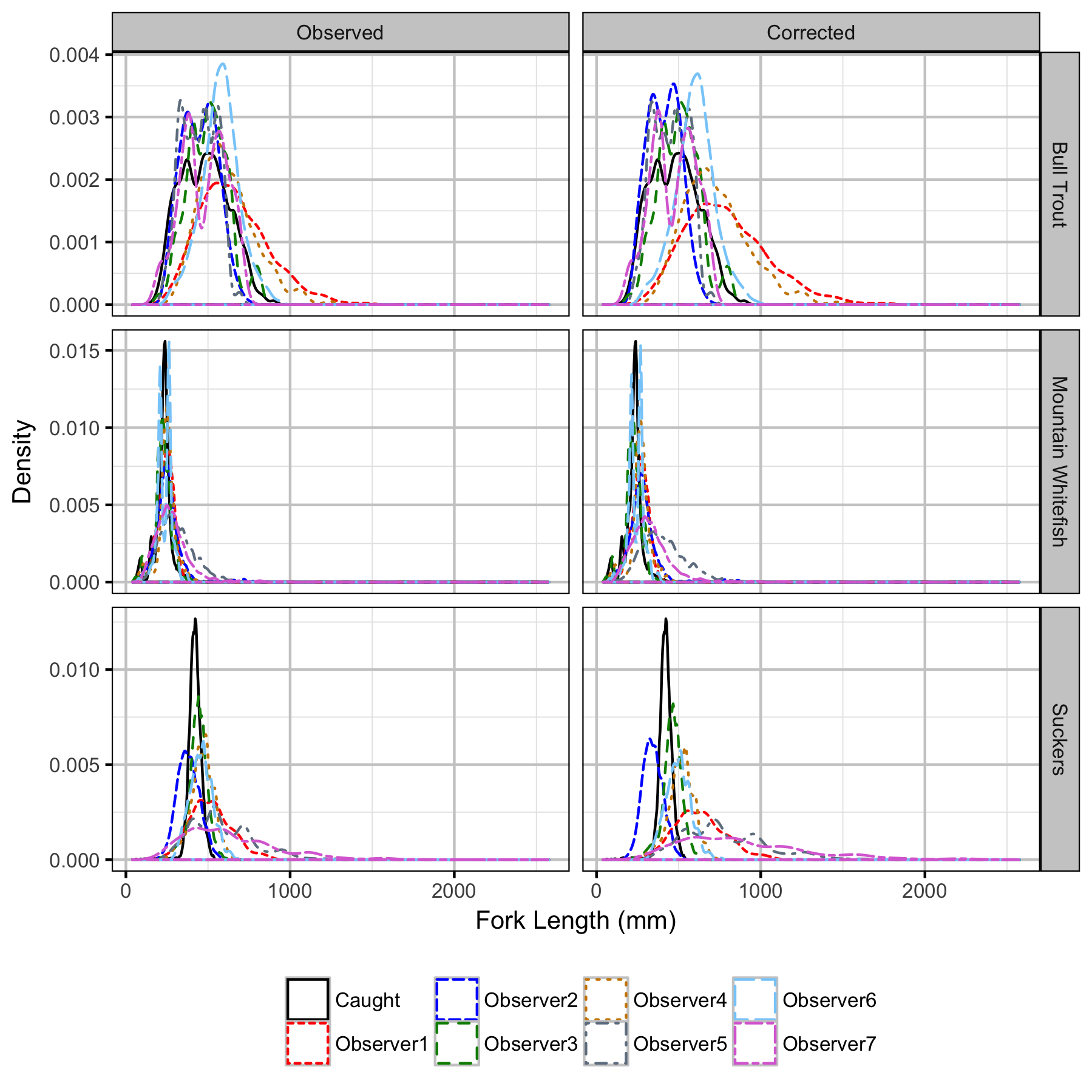
Observer Length Correction
The bias (accuracy) and error (precisions) in observer’s fish length estimates were quantified using a model with a categorical distribution that compared the proportions of fish in different length-classes for each observer to the equivalent proportions for the measured fish.
Key assumptions of the observer length correction model include:
- The expected length bias can vary by observer.
- The expected length error can vary by observer.
- The residual variation in length is independently and identically normally distributed.
The observed fish lengths were corrected for the estimated length biases.
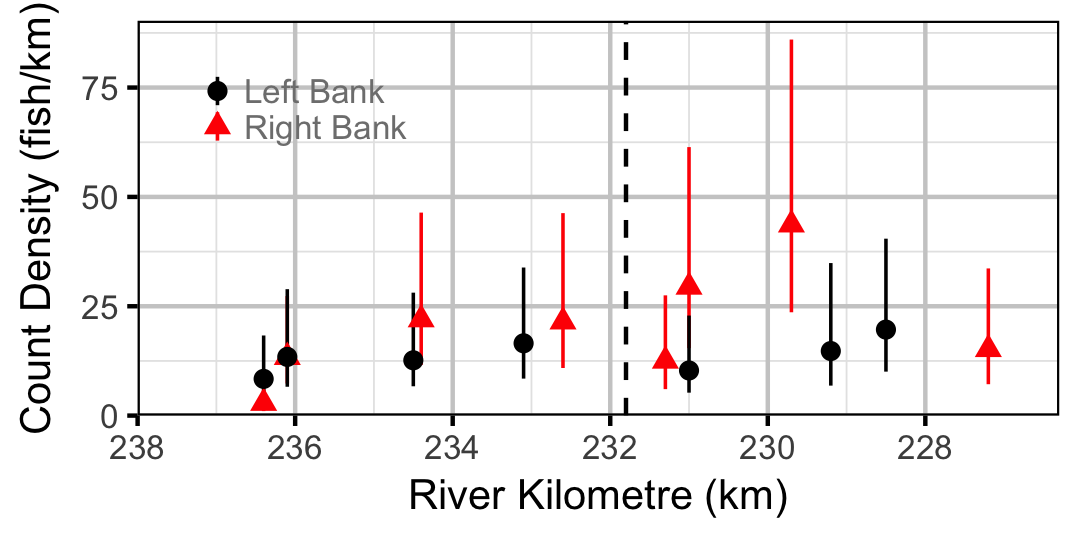
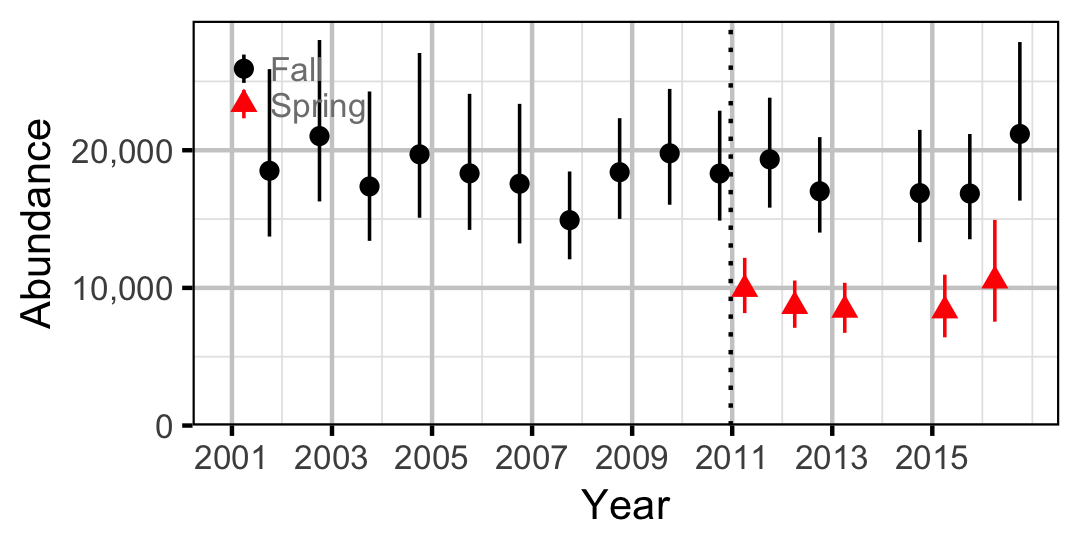
Abundance
The catch and geo-referenced count data were analysed using a capture-recapture-based overdispersed gamma-Poisson model to provide estimates of capture efficiency and absolute abundance. To maximize the number of recaptures the model grouped all the sites into a supersite for the purposes of estimating the number of marked fish but analysed the total captures at the site level.
Key assumptions of the full abundance model include:
- Lineal density (fish/km) varies by season.
- Lineal density varies randomly with site and the interaction between site and year.
- Lineal density varies by river km (distribution).
- The effect of river km on lineal density varies with discharge regime and season.
- The effect of river km on lineal density varies randomly with year.
- Lineal density varies by year as a first-order autoregressive term.
- The change in the annual lineal density varies by discharge regime.
- The change in the annual lineal density varies randomly by year.
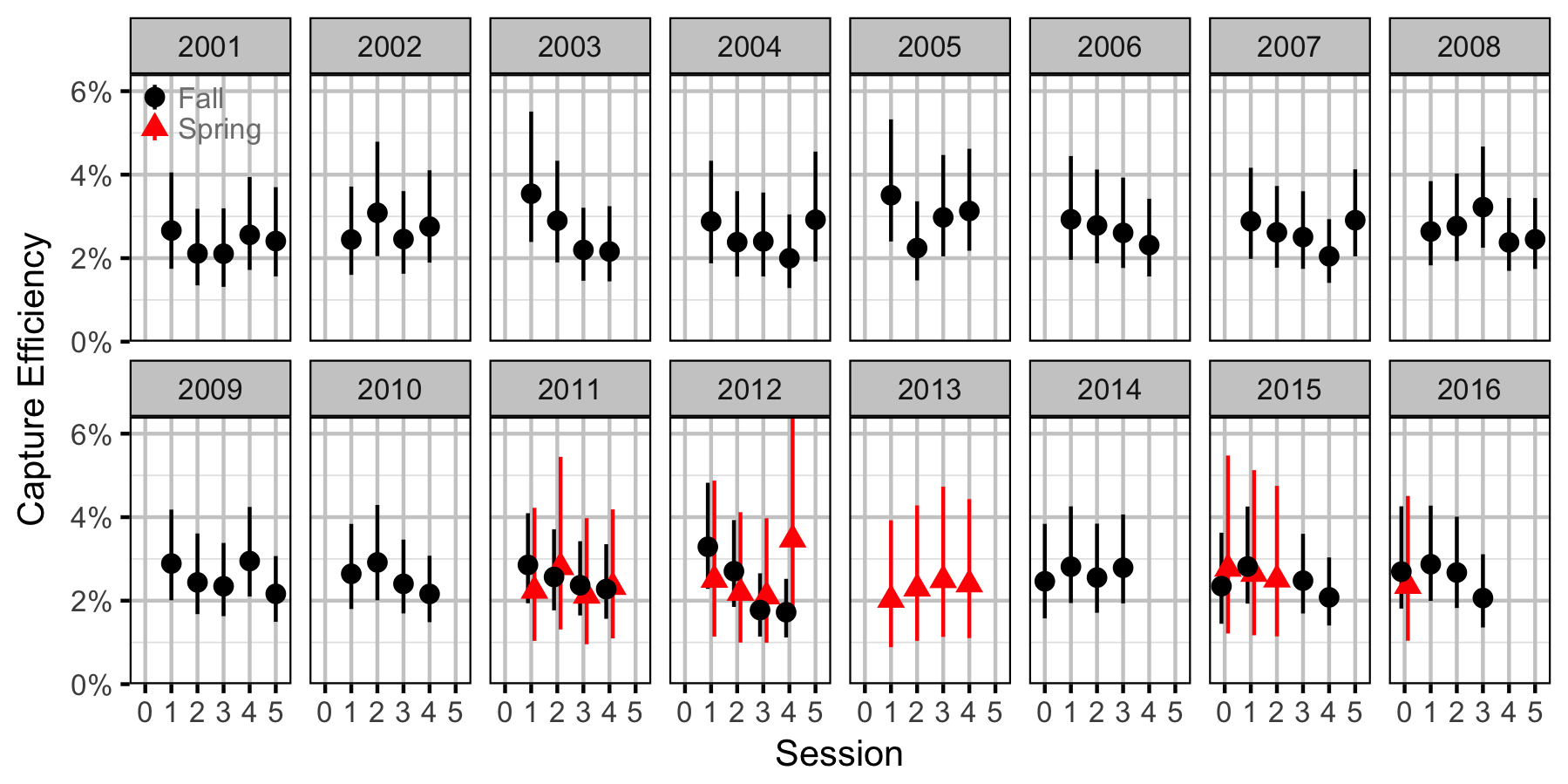
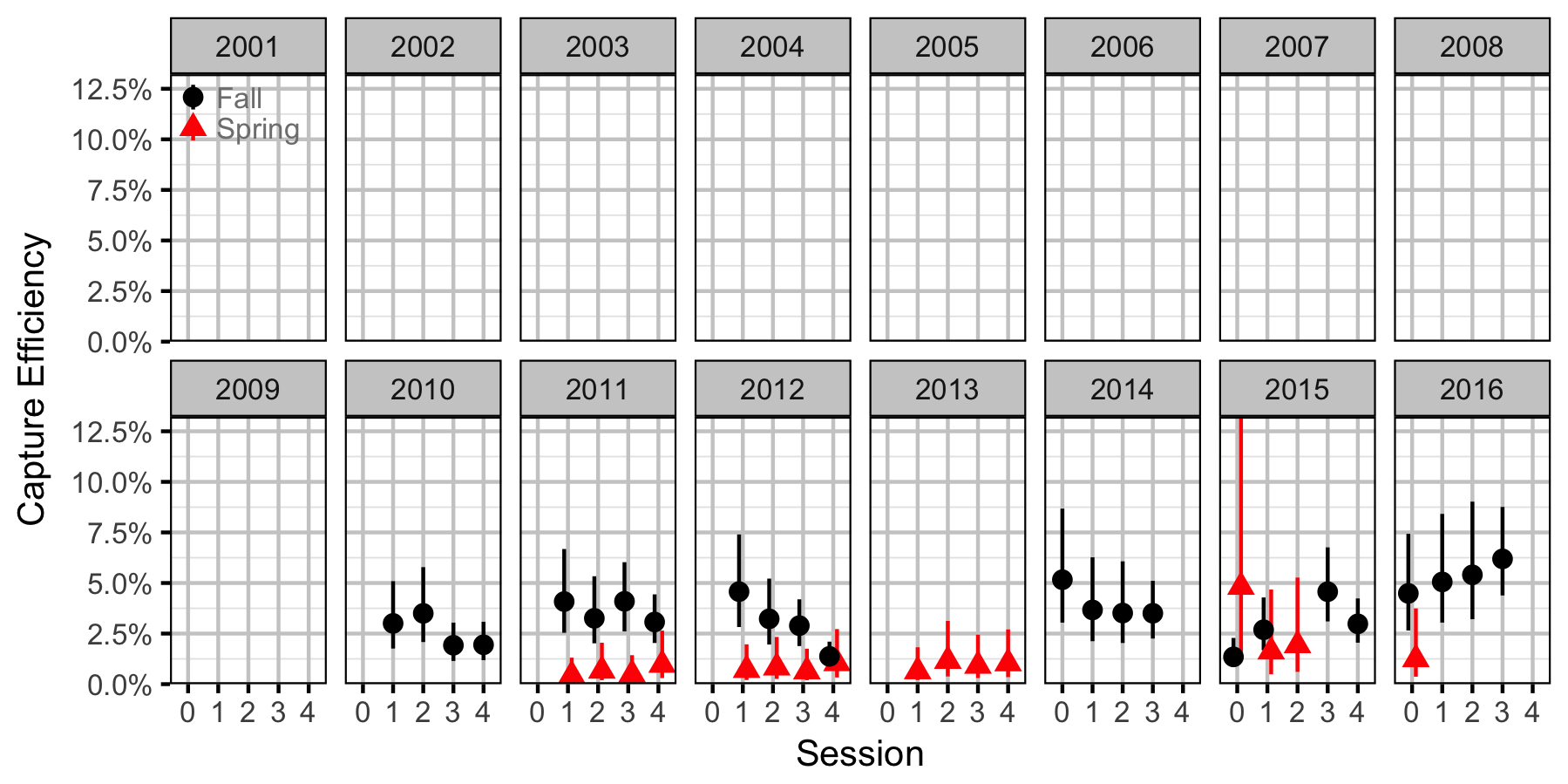
- Efficiency (probability of capture) varies by season and method (capture versus count).
- Efficiency varies randomly by session within season within year.
- Marked and unmarked fish have the same probability of capture.
- Observed fish are encountered at a different rate to captured fish.
- There is no tag loss, migration (at the supersite level), mortality or misidentification of fish.
- The number of fish caught is gamma-Poisson distributed.
- The overdispersion varies by encounter type (count versus capture).
Adult Large-Scale Suckers and Adult Rainbow Trout were analysed using a reduced model with 1) no effect of regime or river km on lineal density; 2) no difference in the error or efficiency between encounter types and 3) no autoregressive component, i.e., with the lineal density varying randomly by year as a straight random effect.
Species Evenness
The site and year estimates of the lineal bank count densities from the count model for Rainbow Trout, Suckers, Burbot and Northern Pikeminnow were combined with the equivalent count estimates for Bull Trout and Adult Mountain Whitefish from the abundance model to calculate the shannon index of evenness \((E)\). The index was calculated using the following formula where \(S\) is the number of species and \(p_i\) is the proportion of the total count belonging to the ith species.
\[ E = \frac{-\sum p_i \log(p_i)}{\log(S)}\]
Model Templates
Growth
model {
bKIntercept ~ dnorm (0, 5^-2)
bKRegime[1] <- 0
for(i in 2:nRegime) {
bKRegime[i] ~ dnorm(0, 5^-2)
}
sKYear ~ dunif (0, 5)
for (i in 1:nYear) {
bKYear[i] ~ dnorm(0, sKYear^-2)
bK[i] <- exp(bKIntercept + bKRegime[step(i - Threshold) + 1] + bKYear[i])
}
bLinf ~ dunif(100, 1000)
sGrowth ~ dunif(0, 100)
for (i in 1:length(Year)) {
eGrowth[i] <- (bLinf - LengthAtRelease[i]) * (1 - exp(-sum(bK[Year[i]:(Year[i] + Years[i] - 1)])))
Growth[i] ~ dnorm(eGrowth[i], sGrowth^-2)
}
tGrowth <- bKRegime[2]
..Template 1.
Condition
model {
bWeightIntercept ~ dnorm(5, 5^-2)
bWeightSlope ~ dnorm(3, 5^-2)
bWeightRegimeIntercept[1] <- 0
bWeightRegimeSlope[1] <- 0
for(i in 2:nRegime) {
bWeightRegimeIntercept[i] ~ dnorm(0, 5^-2)
bWeightRegimeSlope[i] ~ dnorm(0, 5^-2)
}
bWeightSeasonIntercept[1] <- 0
bWeightSeasonSlope[1] <- 0
for(i in 2:nSeason) {
bWeightSeasonIntercept[i] ~ dnorm(0, 5^-2)
bWeightSeasonSlope[i] ~ dnorm(0, 5^-2)
}
sWeightYearIntercept ~ dunif(0, 5)
sWeightYearSlope ~ dunif(0, 5)
for(yr in 1:nYear) {
bWeightYearIntercept[yr] ~ dnorm(0, sWeightYearIntercept^-2)
bWeightYearSlope[yr] ~ dnorm(0, sWeightYearSlope^-2)
}
sWeightSiteIntercept ~ dunif(0, 5)
sWeightSiteYearIntercept ~ dunif(0, 5)
for(st in 1:nSite) {
bWeightSiteIntercept[st] ~ dnorm(0, sWeightSiteIntercept^-2)
for(yr in 1:nYear) {
bWeightSiteYearIntercept[st, yr] ~ dnorm(0, sWeightSiteYearIntercept^-2)
}
}
sWeight ~ dunif(0, 5)
for(i in 1:length(Year)) {
eWeightIntercept[i] <- bWeightIntercept + bWeightRegimeIntercept[Regime[i]] + bWeightSeasonIntercept[Season[i]] + bWeightYearIntercept[Year[i]] + bWeightSiteIntercept[Site[i]] + bWeightSiteYearIntercept[Site[i],Year[i]]
eWeightSlope[i] <- bWeightSlope + bWeightRegimeSlope[Regime[i]] + bWeightSeasonSlope[Season[i]] + bWeightYearSlope[Year[i]]
log(eWeight[i]) <- eWeightIntercept[i] + eWeightSlope[i] * LogLength[i]
Weight[i] ~ dlnorm(log(eWeight[i]) , sWeight^-2)
}
tCondition1 <- bWeightRegimeIntercept[2]
tCondition2 <- bWeightRegimeSlope[2]
..Template 2.
Occupancy
model {
bOccupancySeason[1] <- 0
for(i in 2:nSeason) {
bOccupancySeason[i] ~ dnorm(0, 5^-2)
sOccupancySite ~ dunif(0, 5)
for (st in 1:nSite) {
bOccupancySite[st] ~ dnorm(0, sOccupancySite^-2)
bRate ~ dnorm(0, 5^-2)
sRateYear ~ dunif(0, 5)
for(i in 1:nYear) {
bRateYear[i] ~ dnorm(0, sRateYear^-2)
bRateRegime[1] <- 0
for(i in 2:nRegime) {
bRateRegime[i] ~ dnorm(0, 5^-2)
bOccupancyYear[1] ~ dnorm(0, 5^-2)
for (i in 2:nYear) {
eRateYear[i-1] <- bRate + bRateYear[i-1] + bRateRegime[YearRegime[i-1]]
bOccupancyYear[i] <- bOccupancyYear[i-1] + eRateYear[i-1]
for (i in 1:length(Year)) {
logit(eObserved[i]) <- bOccupancyYear[Year[i]] + bOccupancySeason[Season[i]] + bOccupancySite[Site[i]]
Observed[i] ~ dbern(eObserved[i])
}
..Template 3.
Count
model {
bRateRegime[1] <- 0
for(i in 2:nRegime) {
bRateRegime[i] ~ dnorm(0, 5^-2)
}
bDensitySeason[1] <- 0
for(i in 2:nSeason) {
bDensitySeason[i] ~ dnorm(0, 5^-2)
}
bRate ~ dnorm(0, 5^-2)
sRateYear ~ dunif(0, 5)
for(i in 1:nYear) {
bRateYear[i] ~ dnorm(0, sRateYear^-2)
}
bDensityYear[1] ~ dnorm(0, 5^-2)
for (i in 2:nYear) {
eRateYear[i-1] <- bRate + bRateYear[i-1] + bRateRegime[YearRegime[i-1]]
bDensityYear[i] <- bDensityYear[i-1] + eRateYear[i-1]
}
sDensitySite ~ dunif(0, 5)
sDensitySiteYear ~ dunif(0, 2)
for (i in 1:nSite) {
bDensitySite[i] ~ dnorm(0, sDensitySite^-2)
for (j in 1:nYear) {
bDensitySiteYear[i, j] ~ dnorm(0, sDensitySiteYear^-2)
}
}
sDispersion ~ dunif(0, 5)
for (i in 1:length(Year)) {
log(eDensity[i]) <- bDensityYear[Year[i]] + bDensitySeason[Season[i]] + bDensitySite[Site[i]] + bDensitySiteYear[Site[i],Year[i]]
eCount[i] <- eDensity[i] * SiteLength[i] * ProportionSampled[i]
eDispersion[i] ~ dgamma(1 / sDispersion^2, 1 / sDispersion^2)
Count[i] ~ dpois(eCount[i] * eDispersion[i])
}
tCount <- bRateRegime[2]
..Template 4.
Movement
model {
bMoved ~ dnorm(0, 5^-2)
bLength ~ dnorm(0, 5^-2)
bMovedSeason[1] <- 0
bLengthSeason[1] <- 0
for(i in 2:nSeason) {
bMovedSeason[i] ~ dnorm(0, 5^-5)
bLengthSeason[i] ~ dnorm(0, 5^-5)
}
for (i in 1:length(Season)) {
logit(eMoved[i]) <- bMoved + bMovedSeason[Season[i]] + (bLength + bLengthSeason[Season[i]]) * Length[i]
Moved[i] ~ dbern(eMoved[i])
}
..Template 5.
Observer Length Correction
model {
for(i in 1:nClass) {
dClass[i] <- 1
}
pClass[1:nClass] ~ ddirch(dClass[])
bLength[1] <- 1
sLength[1] <- 1
for(i in 2:nObserver) {
bLength[i] ~ dunif(0.5, 2)
sLength[i] ~ dunif(1, 50)
}
for(i in 1:length(Length)) {
eClass[i] ~ dcat(pClass[])
eLength[i] <- bLength[Observer[i]] * ClassLength[eClass[i]]
eSLength[i] <- sLength[Observer[i]] * ClassSD
Length[i] ~ dnorm(eLength[i], eSLength[i]^-2)
}
..Template 6.
Abundance
model {
bEfficiency ~ dnorm(0, 5^-2)
bDistribution ~ dnorm(0, 5^-2)
bRateRegime[1] <- 0
bDistributionRegime[1] <- 0
for(i in 2:nRegime) {
bRateRegime[i] ~ dnorm(0, 5^-2)
bDistributionRegime[i] ~ dnorm(0, 5^-2)
}
bEfficiencySeason[1] <- 0
bDensitySeason[1] <- 0
bDistributionSeason[1] <- 0
for(i in 2:nSeason) {
bEfficiencySeason[i] ~ dnorm(0, 5^-2)
bDensitySeason[i] ~ dnorm(0, 5^-2)
bDistributionSeason[i] ~ dnorm(0, 5^-2)
}
bRate ~ dnorm(0, 5^-2)
sRateYear ~ dunif(0, 5)
for(i in 1:nYear) {
bRateYear[i] ~ dnorm(0, sRateYear^-2)
}
bDensityYear[1] ~ dnorm(0, 5^-2)
for (i in 2:nYear) {
eRateYear[i-1] <- bRate + bRateYear[i-1] + bRateRegime[YearRegime[i-1]]
bDensityYear[i] <- bDensityYear[i-1] + eRateYear[i-1]
}
sDistributionYear ~ dunif(0, 2)
for (i in 1:nYear) {
bDistributionYear[i] ~ dnorm(0, sDistributionYear^-2)
}
sDensitySite ~ dunif(0, 5)
sDensitySiteYear ~ dunif(0, 2)
for (i in 1:nSite) {
bDensitySite[i] ~ dnorm(0, sDensitySite^-2)
for (j in 1:nYear) {
bDensitySiteYear[i, j] ~ dnorm(0, sDensitySiteYear^-2)
}
}
sEfficiencySessionSeasonYear ~ dunif(0, 5)
for (i in 1:nSession) {
for (j in 1:nSeason) {
for (k in 1:nYear) {
bEfficiencySessionSeasonYear[i, j, k] ~ dnorm(0, sEfficiencySessionSeasonYear^-2)
}
}
}
bMultiplier <- 0
sDispersion ~ dnorm(0, 2^-2)
bMultiplierType[1] <- 0
sDispersionType[1] <- 0
for (i in 2:nType) {
bMultiplierType[i] ~ dnorm(0, 2^-2)
sDispersionType[i] ~ dnorm(0, 2^-2)
}
for(i in 1:length(EffIndex)) {
logit(eEff[i]) <- bEfficiency + bEfficiencySeason[Season[EffIndex[i]]] + bEfficiencySessionSeasonYear[Session[EffIndex[i]],Season[EffIndex[i]],Year[EffIndex[i]]]
Marked[EffIndex[i]] ~ dbin(eEff[i], Tagged[EffIndex[i]])
}
for (i in 1:length(Year)) {
logit(eEfficiency[i]) <- bEfficiency + bEfficiencySeason[Season[i]] + bEfficiencySessionSeasonYear[Session[i], Season[i], Year[i]]
eDistribution[i] <- bDistribution + bDistributionRegime[Regime[i]] + bDistributionSeason[Season[i]] + bDistributionYear[Year[i]]
log(eDensity[i]) <- bDensityYear[Year[i]] + eDistribution[i] * RiverKm[i]
+ bDensitySeason[Season[i]] + bDensitySite[Site[i]] + bDensitySiteYear[Site[i], Year[i]]
log(eMultiplier[i]) <- bMultiplier + bMultiplierType[Type[i]]
eCatch[i] <- eDensity[i] * SiteLength[i] * ProportionSampled[i] * eEfficiency[i] * eMultiplier[i]
log(esDispersion[i]) <- sDispersion + sDispersionType[Type[i]]
eDispersion[i] ~ dgamma(esDispersion[i]^-2 + 0.1, esDispersion[i]^-2 + 0.1)
Catch[i] ~ dpois(eCatch[i] * eDispersion[i])
}
tAbundance <- bRateRegime[2]
tDistribution <- bDistributionRegime[2]
..Template 7.
Results
Tables
Growth
Table 2. Parameter descriptions.
| Parameter | Description |
|---|---|
bK[i] |
Expected growth coefficient in the ith year |
bKIntercept |
Intercept for log(bK) |
bKRegime[i] |
Effect of ith regime on log(bK) |
bKYear[i] |
Random effect of ith Year on log(bK) |
bLinf |
Mean maximum length |
eGrowth[i] |
Expected Growth of the ith recapture |
Growth[i] |
Change in length of the ith fish between release and recapture |
LengthAtRelease[i] |
Length of the ith recapture when released |
nRegime[i] |
Number of regimes |
sGrowth |
SD of residual variation in Growth |
sKYear[i] |
SD of effect of Year on log(bK) |
Threshold |
Last year of the first regime |
Year[i] |
Year the ith recapture was released |
Years[i] |
Number of years between release and recapture for the ith recapture |
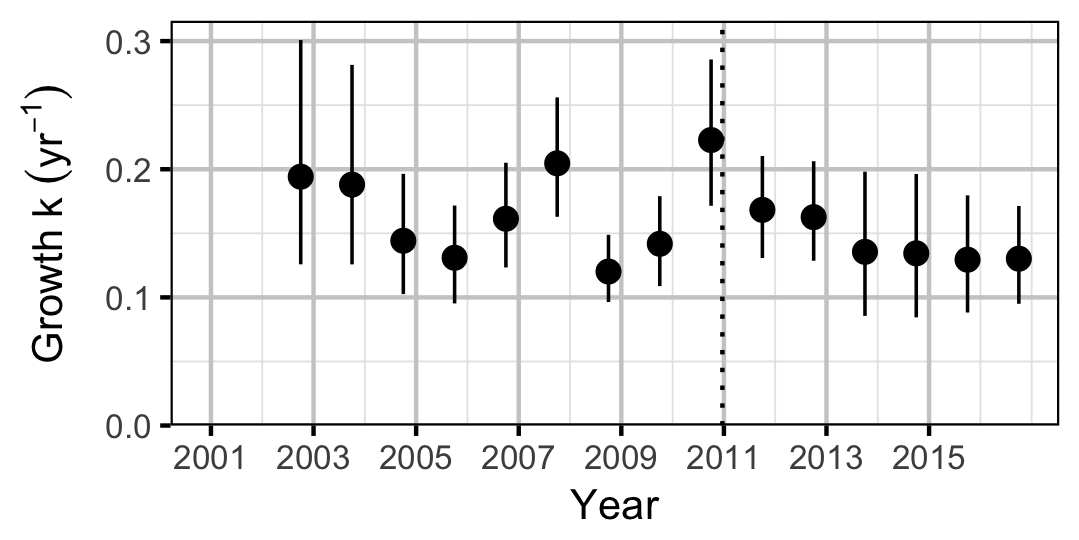
Bull Trout
Table 3. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -1.8641739 | 0.1054579 | -17.7080475 | -2.0727196 | -1.661006 | 0.0005 |
| bKRegime[2] | 0.1068986 | 4.9147096 | 0.0093809 | -9.2812376 | 9.516509 | 0.9860 |
| bLinf | 857.8394479 | 28.6424411 | 30.0296806 | 808.8380004 | 920.834623 | 0.0005 |
| sGrowth | 31.1828861 | 1.4089127 | 22.1873377 | 28.5533490 | 34.191604 | 0.0005 |
| sKYear | 0.2493117 | 0.0752564 | 3.4608626 | 0.1432783 | 0.437170 | 0.0005 |
| tGrowth | 0.1068986 | 4.9147096 | 0.0093809 | -9.2812376 | 9.516509 | 0.9860 |
Table 4. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 260 | 6 | 2000 | 4 | 40000 | 7.916979 | 1 | TRUE |
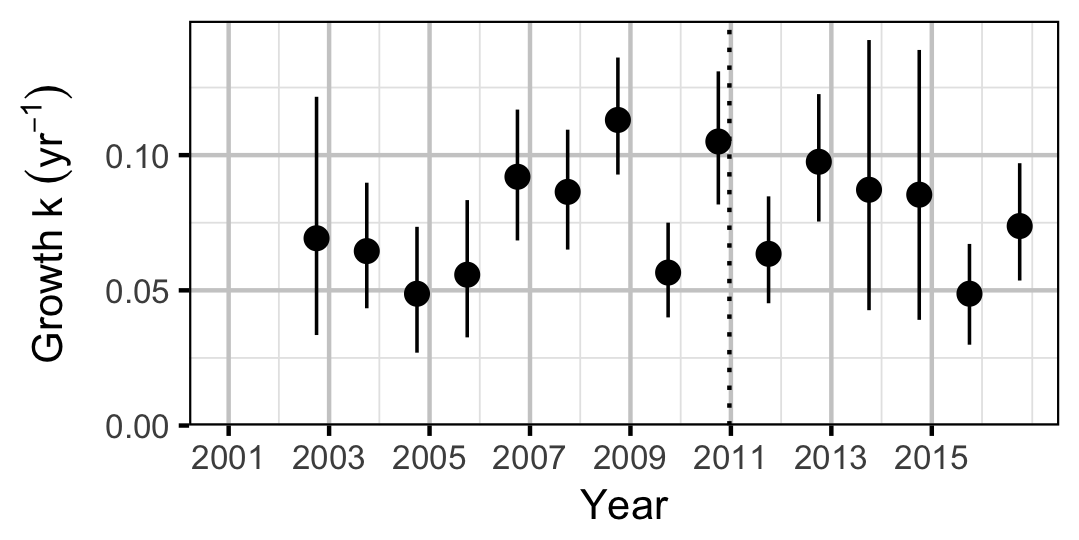
Mountain Whitefish
Table 5. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -2.6127914 | 0.1352452 | -19.3441983 | -2.8905518 | -2.3589141 | 0.0005 |
| bKRegime[2] | -0.1442619 | 4.9119432 | -0.0419278 | -9.6515815 | 9.5267152 | 0.9730 |
| bLinf | 355.1710280 | 8.1490568 | 43.6293579 | 340.7860764 | 372.5956513 | 0.0005 |
| sGrowth | 10.6877991 | 0.2428641 | 44.0263825 | 10.2439891 | 11.1882805 | 0.0005 |
| sKYear | 0.3505649 | 0.1112995 | 3.3281477 | 0.2104646 | 0.6355877 | 0.0005 |
| tGrowth | -0.1442619 | 4.9119432 | -0.0419278 | -9.6515815 | 9.5267152 | 0.9730 |
Table 6. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1000 | 6 | 2000 | 4 | 40000 | 29.70091 | 1.01 | TRUE |
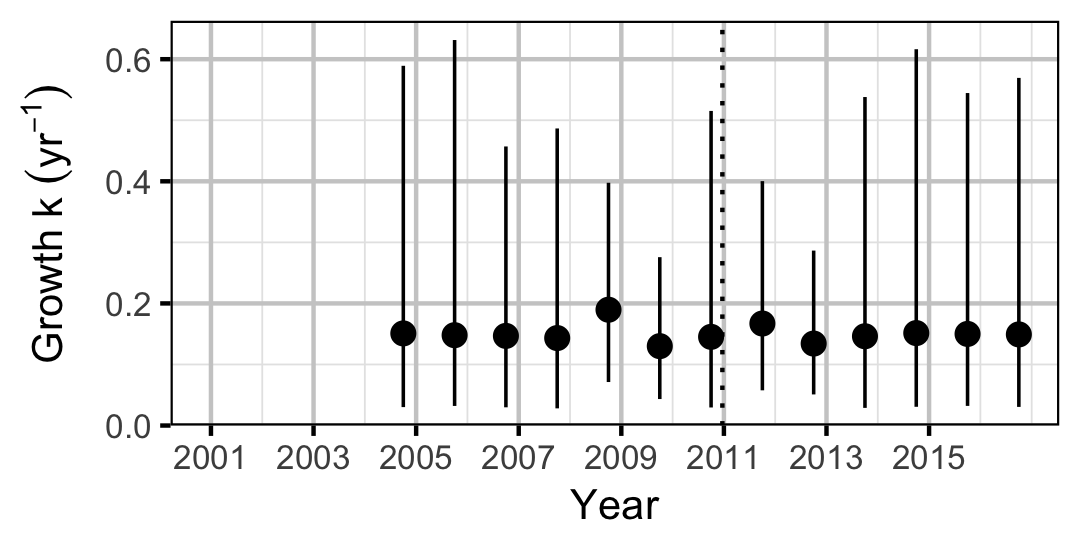
Rainbow Trout
Table 7. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bKIntercept | -1.8943749 | 0.4945770 | -3.9365546 | -2.9571878 | -1.116554 | 0.0005 |
| bKRegime[2] | 0.0560165 | 4.9793517 | 0.0015026 | -9.8213993 | 10.068428 | 0.9880 |
| bLinf | 571.8868548 | 132.6802529 | 4.5985788 | 438.8368763 | 945.168842 | 0.0005 |
| sGrowth | 25.3967997 | 6.2181659 | 4.2508564 | 17.1872513 | 41.000639 | 0.0005 |
| sKYear | 0.3052896 | 0.3990389 | 1.0444827 | 0.0297265 | 1.494123 | 0.0005 |
| tGrowth | 0.0560165 | 4.9793517 | 0.0015026 | -9.8213993 | 10.068428 | 0.9880 |
Table 8. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 16 | 6 | 2000 | 4 | 40000 | 0.7223349 | 1.03 | TRUE |
Condition
Table 9. Parameter descriptions.
| Parameter | Description |
|---|---|
bWeightIntercept |
Intercept for eWeightIntercept |
bWeightRegimeIntercept[i] |
Effect of ith regime on bWeightIntercept |
bWeightRegimeSlope[i] |
Effect of ith regime on bWeightSlope |
bWeightSeasonIntercept[i] |
Effect of ith season on bWeightIntercept |
bWeightSeasonSlope[i] |
Effect of ith season on bWeightSlope |
bWeightSiteIntercept[i] |
Random effect of ith site on bWeightIntercept |
bWeightSiteYearIntercept[i,j] |
Random effect of ith site in jth year on bWeightIntercept |
bWeightSlope |
Intercept for eWeightSlope |
bWeightYearIntercept[i] |
Random effect of ith year on bWeightIntercept |
bWeightYearSlope[i] |
Random effect of ith year on bWeightSlope |
eWeight[i] |
Expected weight of the ith fish |
eWeightIntercept[i] |
Intercept for log(eWeight[i]) |
eWeightSlope[i] |
Slope for log(eWeight[i]) |
Length[i] |
Length of ith fish |
sWeight |
Residual SD of Weight |
sWeightSiteIntercept |
SD for the effect of site on bWeightIntercept |
sWeightSiteYearIntercept |
SD for the effect of the combination of site and year on eWeightIntercept |
sWeightYearIntercept |
SD of the effect of year on bWeightIntercept |
sWeightYearSlope |
SD for the random effect of year on eWeightSlope |
Weight[i] |
Weight of ith fish |
Bull Trout
Table 10. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 6.8224727 | 0.0184439 | 369.8938491 | 6.7839311 | 6.8584054 | 0.0005 |
| bWeightRegimeIntercept[2] | -0.1061049 | 0.0286127 | -3.6768983 | -0.1595558 | -0.0450472 | 0.0005 |
| bWeightRegimeSlope[2] | 0.0457349 | 0.0571055 | 0.8369983 | -0.0623809 | 0.1626876 | 0.3690 |
| bWeightSeasonIntercept[2] | 0.0014480 | 0.0092923 | 0.1386271 | -0.0167606 | 0.0197889 | 0.8630 |
| bWeightSeasonSlope[2] | 0.0116925 | 0.0236088 | 0.4968422 | -0.0335823 | 0.0584057 | 0.6110 |
| bWeightSlope | 3.1612666 | 0.0374257 | 84.4896154 | 3.0857082 | 3.2373123 | 0.0005 |
| sWeight | 0.1372626 | 0.0018490 | 74.2445946 | 0.1337674 | 0.1408549 | 0.0005 |
| sWeightSiteIntercept | 0.0110831 | 0.0057811 | 1.9514451 | 0.0011294 | 0.0240219 | 0.0005 |
| sWeightSiteYearIntercept | 0.0173022 | 0.0054113 | 3.1187082 | 0.0039206 | 0.0264252 | 0.0005 |
| sWeightYearIntercept | 0.0498527 | 0.0123718 | 4.1864850 | 0.0331467 | 0.0821260 | 0.0005 |
| sWeightYearSlope | 0.0974516 | 0.0256138 | 3.9272937 | 0.0614732 | 0.1602472 | 0.0005 |
| tCondition1 | -0.1061049 | 0.0286127 | -3.6768983 | -0.1595558 | -0.0450472 | 0.0005 |
| tCondition2 | 0.0457349 | 0.0571055 | 0.8369983 | -0.0623809 | 0.1626876 | 0.3690 |
Table 11. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 3013 | 13 | 2000 | 4 | 640000 | 7361.41509962082s (~2.04 hours) | 1.02 | TRUE |
Mountain Whitefish
Table 12. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 4.7881401 | 0.0082425 | 580.9473113 | 4.7730303 | 4.8056091 | 0.0005 |
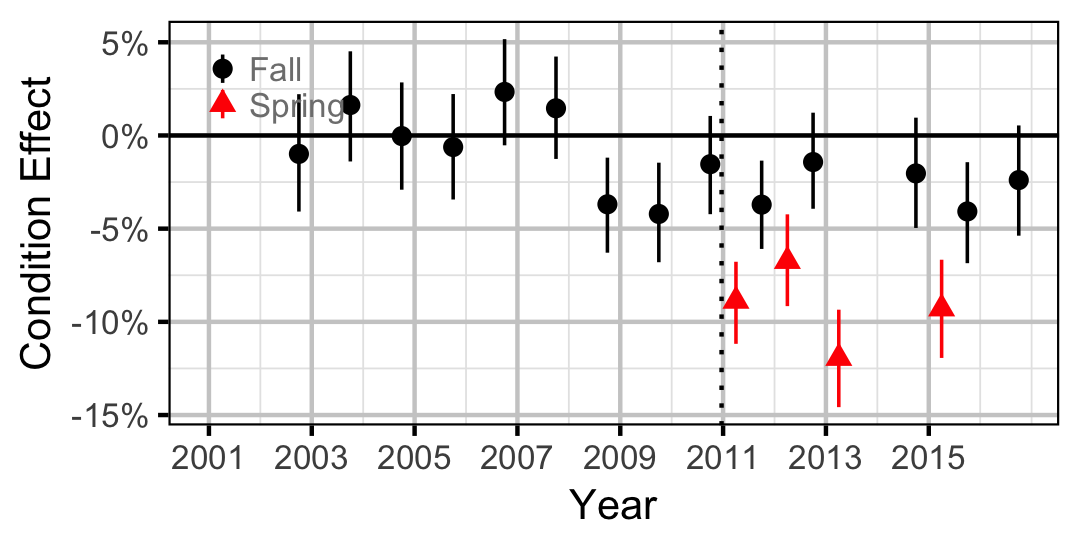
| bWeightRegimeIntercept[2] | -0.0382501 | 0.0123472 | -3.1213338 | -0.0634617 | -0.0153703 | 0.0050 |
| bWeightRegimeSlope[2] | -0.0257996 | 0.0270373 | -0.9529919 | -0.0810421 | 0.0268842 | 0.3110 |
| bWeightSeasonIntercept[2] | -0.0444107 | 0.0039602 | -11.2071809 | -0.0523081 | -0.0365914 | 0.0005 |
| bWeightSeasonSlope[2] | -0.1015766 | 0.0175103 | -5.7976748 | -0.1353067 | -0.0666228 | 0.0005 |
| bWeightSlope | 3.2101925 | 0.0177418 | 180.9159728 | 3.1742461 | 3.2445277 | 0.0005 |
| sWeight | 0.0985979 | 0.0008188 | 120.4330214 | 0.0969835 | 0.1001991 | 0.0005 |
| sWeightSiteIntercept | 0.0062915 | 0.0027945 | 2.3246821 | 0.0013797 | 0.0126423 | 0.0005 |
| sWeightSiteYearIntercept | 0.0135861 | 0.0018326 | 7.4197902 | 0.0101365 | 0.0172210 | 0.0005 |
| sWeightYearIntercept | 0.0228453 | 0.0059260 | 4.0204448 | 0.0152810 | 0.0382084 | 0.0005 |
| sWeightYearSlope | 0.0423574 | 0.0139876 | 3.1614422 | 0.0226610 | 0.0759205 | 0.0005 |
| tCondition1 | -0.0382501 | 0.0123472 | -3.1213338 | -0.0634617 | -0.0153703 | 0.0050 |
| tCondition2 | -0.0257996 | 0.0270373 | -0.9529919 | -0.0810421 | 0.0268842 | 0.3110 |
Table 13. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 7458 | 13 | 2000 | 4 | 40000 | 1338.432 | 1.02 | TRUE |
Rainbow Trout
Table 14. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 4.6176353 | 0.0153242 | 301.3392645 | 4.5888573 | 4.6487672 | 0.0005 |
| bWeightRegimeIntercept[2] | -0.0105954 | 0.0212952 | -0.5219893 | -0.0560419 | 0.0289769 | 0.5840 |
| bWeightRegimeSlope[2] | -0.0342521 | 0.0572297 | -0.6200595 | -0.1476211 | 0.0723243 | 0.5300 |
| bWeightSeasonIntercept[2] | -0.0682439 | 0.0146064 | -4.6786801 | -0.0963354 | -0.0401625 | 0.0005 |
| bWeightSeasonSlope[2] | 0.0042373 | 0.0408189 | 0.1270415 | -0.0713895 | 0.0888590 | 0.9080 |
| bWeightSlope | 3.0907217 | 0.0373988 | 82.7121557 | 3.0239487 | 3.1700691 | 0.0005 |
| sWeight | 0.1080384 | 0.0035052 | 30.8339165 | 0.1011158 | 0.1151982 | 0.0005 |
| sWeightSiteIntercept | 0.0171618 | 0.0114959 | 1.6089359 | 0.0007372 | 0.0454984 | 0.0005 |
| sWeightSiteYearIntercept | 0.0195131 | 0.0108562 | 1.8618730 | 0.0029640 | 0.0416312 | 0.0005 |
| sWeightYearIntercept | 0.0217561 | 0.0134809 | 1.7602155 | 0.0029458 | 0.0545759 | 0.0005 |
| sWeightYearSlope | 0.0733275 | 0.0263202 | 2.9585403 | 0.0385498 | 0.1391262 | 0.0005 |
| tCondition1 | -0.0105954 | 0.0212952 | -0.5219893 | -0.0560419 | 0.0289769 | 0.5840 |
| tCondition2 | -0.0342521 | 0.0572297 | -0.6200595 | -0.1476211 | 0.0723243 | 0.5300 |
Table 15. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 546 | 13 | 2000 | 4 | 80000 | 86.5664749145508s (~1.44 minutes) | 1.07 | TRUE |
Largescale Sucker
Table 16. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeightIntercept | 6.8090532 | 0.0315213 | 216.065780 | 6.7533875 | 6.8741236 | 5e-04 |
| bWeightSeasonIntercept[2] | 0.0214070 | 0.0054512 | 3.914817 | 0.0111581 | 0.0319266 | 5e-04 |
| bWeightSeasonSlope[2] | 0.1753231 | 0.0477888 | 3.647121 | 0.0782321 | 0.2657080 | 5e-04 |
| bWeightSlope | 2.8715268 | 0.1148855 | 24.992947 | 2.6488541 | 3.0997607 | 5e-04 |
| sWeight | 0.0824593 | 0.0012222 | 67.514292 | 0.0801789 | 0.0850479 | 5e-04 |
| sWeightSiteIntercept | 0.0058696 | 0.0035599 | 1.721824 | 0.0003922 | 0.0137578 | 5e-04 |
| sWeightSiteYearIntercept | 0.0099943 | 0.0033401 | 2.914380 | 0.0023342 | 0.0156410 | 5e-04 |
| sWeightYearIntercept | 0.0687345 | 0.0304800 | 2.490380 | 0.0409592 | 0.1434882 | 5e-04 |
| sWeightYearSlope | 0.2447352 | 0.1190849 | 2.303969 | 0.1406327 | 0.5794410 | 5e-04 |
Table 17. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 2303 | 9 | 2000 | 4 | 2560000 | 13246.787014246s (~3.68 hours) | 1.01 | TRUE |
Occupancy
Table 18. Parameter descriptions.
| Parameter | Description |
|---|---|
bOccupancySeason[i] |
Effect of ith season on logit(eOccupancy) |
bOccupancySite[i] |
Effect of ith site on logit(eOccupancy) |
bOccupancyYear[i] |
Effect of ith year on logit(eOccupancy) |
bRate |
Intercept of eRateYear |
bRateRegime[i] |
Effect of ith regime on eRateYear |
bRateYear[i] |
Effect of ith year on eRateYear |
eObserved[i] |
Probability of observing species on ith site visit |
eOccupancy[i] |
Predicted occupancy (species presence versus absence) on ith site visit |
eRateYear[i] |
Change in bOccupancyYear between year i-1 and year i |
nRegime |
Number of regimes in the dataset (2) |
nSeason |
Number of seasons in the dataset (2) |
nSite |
Number of sites in the dataset |
nYear |
Number of years of data |
Observed[i] |
Whether the species was observed on ith site visit (0 or 1) |
Regime[i] |
Regime ofith site visit |
Season[i] |
Season of ith site visit |
Site[i] |
Site of ith site visit |
sOccupancySite |
SD parameter for the distribution of bOccupancySite[i] |
sRateYear |
SD parameter for the distribution of bRateYear |
Year[i] |
Year of ith site visit |
Rainbow Trout
Table 19. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -0.0441430 | 0.2915208 | -0.1708046 | -0.6390309 | 0.4998309 | 0.8820 |
| bRate | 0.1674582 | 0.4529931 | 0.2846738 | -0.9314858 | 0.9347612 | 0.6640 |
| bRateRegime[2] | -0.2266203 | 0.7641868 | -0.2506344 | -1.6226028 | 1.4674321 | 0.7290 |
| sOccupancySite | 2.0798967 | 0.5124052 | 4.2201985 | 1.3927839 | 3.4513820 | 0.0005 |
| sRateYear | 1.1922660 | 0.4346520 | 2.9070743 | 0.6336904 | 2.3222262 | 0.0005 |
Table 20. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 320000 | 268.80225276947s (~4.48 minutes) | 1.01 | TRUE |
Burbot
Table 21. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -0.4620141 | 0.3136597 | -1.496502 | -1.0958380 | 0.1373124 | 0.1340 |
| bRate | 0.4578239 | 0.4878937 | 1.092664 | -0.3184839 | 1.7031044 | 0.2080 |
| bRateRegime[2] | -1.1638224 | 0.7380314 | -1.604433 | -2.8300107 | 0.3062082 | 0.0960 |
| sOccupancySite | 0.9581696 | 0.2568683 | 3.863209 | 0.5895874 | 1.6206694 | 0.0005 |
| sRateYear | 1.0661645 | 0.4140664 | 2.745384 | 0.5268541 | 2.1326053 | 0.0005 |
Table 22. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 160000 | 136.861769199371s (~2.28 minutes) | 1.1 | TRUE |
Lake Whitefish
Table 23. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -4.8610298 | 0.8170743 | -6.0436608 | -6.729908 | -3.5350161 | 0.0005 |
| bRate | 0.2263339 | 0.5772797 | 0.3193839 | -1.000189 | 1.2968137 | 0.6760 |
| bRateRegime[2] | -0.3982608 | 0.9016562 | -0.4806933 | -2.144271 | 1.3748100 | 0.6400 |
| sOccupancySite | 0.4687208 | 0.1709773 | 2.8065144 | 0.176911 | 0.8683258 | 0.0005 |
| sRateYear | 1.7872412 | 0.4652836 | 3.9738154 | 1.141766 | 2.9399117 | 0.0005 |
Table 24. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 160000 | 133.611914157867s (~2.23 minutes) | 1.07 | TRUE |
Northern Pikeminnow
Table 25. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -2.0446042 | 0.4132843 | -4.964727 | -2.8447114 | -1.2730866 | 0.0005 |
| bRate | 0.3893736 | 0.2700138 | 1.481535 | -0.1127161 | 0.9666526 | 0.1160 |
| bRateRegime[2] | -0.4623232 | 0.4427830 | -1.063541 | -1.3694467 | 0.4010425 | 0.2560 |
| sOccupancySite | 1.2954298 | 0.3630245 | 3.712130 | 0.7974610 | 2.1987692 | 0.0005 |
| sRateYear | 0.7211602 | 0.2760132 | 2.767365 | 0.3524526 | 1.3854180 | 0.0005 |
Table 26. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 160000 | 132.825829982758s (~2.21 minutes) | 1.03 | TRUE |
Redside Shiner
Table 27. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -0.9425609 | 0.3646064 | -2.6128776 | -1.7072231 | -0.2768414 | 0.0080 |
| bRate | 0.4374469 | 0.4668138 | 0.9401063 | -0.4845830 | 1.4254734 | 0.3160 |
| bRateRegime[2] | -0.5191104 | 0.8430247 | -0.6537988 | -2.3532710 | 1.1045241 | 0.4790 |
| sOccupancySite | 2.1613548 | 0.5989423 | 3.7590343 | 1.3514431 | 3.7588346 | 0.0005 |
| sRateYear | 1.4990505 | 0.4964205 | 3.1823567 | 0.8319064 | 2.7345524 | 0.0005 |
Table 28. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 320000 | 258.049988031387s (~4.3 minutes) | 1.04 | TRUE |
Sculpins
Table 29. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bOccupancySeason[2] | -0.3573008 | 0.2716340 | -1.318421 | -0.8740651 | 0.1831799 | 0.1790 |
| bRate | 0.4900018 | 0.3408342 | 1.373709 | -0.2558886 | 1.0852118 | 0.1890 |
| bRateRegime[2] | -0.8687456 | 0.7312247 | -1.172275 | -2.2202616 | 0.6533350 | 0.2220 |
| sOccupancySite | 1.2830207 | 0.3115779 | 4.266274 | 0.8582813 | 2.0429250 | 0.0005 |
| sRateYear | 1.3498246 | 0.3537100 | 3.959291 | 0.8564961 | 2.2655003 | 0.0005 |
Table 30. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 5 | 2000 | 4 | 160000 | 141.722540855408s (~2.36 minutes) | 1.07 | TRUE |
Count
Table 31. Parameter descriptions.
| Parameter | Description |
|---|---|
bDensitySeason[i] |
Effect of ith season on log(eDensity) |
bDensitySite[i] |
Effect of ith site on log(eDensity) |
bDensitySiteYear[i, j] |
Effect of ith site in jth year on log(eDensity) |
bDensityYear[i] |
Random effect of ith year on log(eDensity) |
bRate |
Baseline rate of change (relative to the previous year) in eDensity due to year effect |
bRateRegime[i] |
Deviate from bRate due to regime effect in the ith year |
bRateYear[i] |
Random deviate from bRate due to year effect in the ith year |
Count[i] |
Count on ith site visit |
eCount[i] |
Expected count on ith site visit |
eDensity[i] |
Lineal density on ith site visit |
eDispersion[i] |
Overdispersion factor on ith site visit |
eRateYear[i] |
Rate of change in year effect between the (i-1)th and ith year |
ProportionSampled[i] |
Proportion of ith site that was sampled |
sDispersion[i] |
SD of the overdispersion factor distribution |
SiteLength[i] |
Length of ith site |
sRateYear |
SD of the distribution of bRateYear |
Rainbow Trout
Table 32. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -0.0558554 | 0.1581371 | -0.3617073 | -0.3643737 | 0.2662402 | 0.7210 |
| bRate | 0.3097245 | 0.2203194 | 1.4084916 | -0.1392948 | 0.7741460 | 0.1700 |
| bRateRegime[2] | -0.5228539 | 0.4377085 | -1.2193071 | -1.3973239 | 0.3197493 | 0.2060 |
| sDensitySite | 1.6865947 | 0.4212903 | 4.1656691 | 1.1318535 | 2.7494199 | 0.0005 |
| sDensitySiteYear | 0.7651275 | 0.0933484 | 8.2263266 | 0.5961492 | 0.9668685 | 0.0005 |
| sDispersion | 0.8443905 | 0.0574568 | 14.7304306 | 0.7382854 | 0.9631970 | 0.0005 |
| sRateYear | 0.7548222 | 0.2675483 | 2.9365686 | 0.3623827 | 1.3600096 | 0.0005 |
| tCount | -0.5228539 | 0.4377085 | -1.2193071 | -1.3973239 | 0.3197493 | 0.2060 |
Table 33. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 8 | 2000 | 4 | 8e+05 | 4211.07110714912s (~1.17 hours) | 1.04 | TRUE |
Burbot
Table 34. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -0.7008740 | 0.2829301 | -2.4583869 | -1.2222639 | -0.1576417 | 0.0150 |
| bRate | 0.3457599 | 0.4179139 | 0.8351192 | -0.5379906 | 1.1403800 | 0.3660 |
| bRateRegime[2] | -1.0494175 | 0.7563619 | -1.3667513 | -2.5285938 | 0.6490754 | 0.1530 |
| sDensitySite | 0.7770214 | 0.2460972 | 3.3195278 | 0.4582638 | 1.4287828 | 0.0005 |
| sDensitySiteYear | 0.4302179 | 0.1930011 | 2.1941856 | 0.0573630 | 0.7871522 | 0.0005 |
| sDispersion | 1.2101743 | 0.1418903 | 8.5651207 | 0.9409837 | 1.5045709 | 0.0005 |
| sRateYear | 1.2128722 | 0.4244377 | 3.0165039 | 0.6137706 | 2.3191154 | 0.0005 |
| tCount | -1.0494175 | 0.7563619 | -1.3667513 | -2.5285938 | 0.6490754 | 0.1530 |
Table 35. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 8 | 2000 | 4 | 8e+05 | 4453.63915920258s (~1.24 hours) | 1.04 | TRUE |
Northern Pikeminnow
Table 36. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -2.1944847 | 0.4198386 | -5.258263 | -3.0621880 | -1.3987577 | 0.0005 |
| bRate | 0.3782332 | 0.2290669 | 1.665998 | -0.0723541 | 0.8551925 | 0.0940 |
| bRateRegime[2] | -0.4745792 | 0.4315332 | -1.104948 | -1.4151222 | 0.3749522 | 0.2260 |
| sDensitySite | 1.2618458 | 0.3686478 | 3.558548 | 0.7418742 | 2.1712440 | 0.0005 |
| sDensitySiteYear | 0.7494810 | 0.1873177 | 3.979125 | 0.3547730 | 1.1086029 | 0.0005 |
| sDispersion | 1.3409528 | 0.1319098 | 10.200577 | 1.1030656 | 1.6164564 | 0.0005 |
| sRateYear | 0.6680811 | 0.2510400 | 2.828973 | 0.3459029 | 1.3331360 | 0.0005 |
| tCount | -0.4745792 | 0.4315332 | -1.104948 | -1.4151222 | 0.3749522 | 0.2260 |
Table 37. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 8 | 2000 | 4 | 4e+05 | 1737.69567394257s (~28.96 minutes) | 1.06 | TRUE |
Suckers
Table 38. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -0.1043625 | 0.1084576 | -0.9767647 | -0.3150610 | 0.0997476 | 0.3410 |
| bRate | 0.0272163 | 0.2049856 | 0.2073784 | -0.3128084 | 0.4364884 | 0.8670 |
| bRateRegime[2] | -0.1173087 | 0.3499090 | -0.3202261 | -0.7991742 | 0.5485687 | 0.7600 |
| sDensitySite | 0.5379528 | 0.1409113 | 3.9748213 | 0.3531519 | 0.8806989 | 0.0005 |
| sDensitySiteYear | 0.5355914 | 0.0559827 | 9.6034547 | 0.4333479 | 0.6506571 | 0.0005 |
| sDispersion | 0.8414728 | 0.0258002 | 32.6535746 | 0.7936624 | 0.8939800 | 0.0005 |
| sRateYear | 0.6234944 | 0.1739960 | 3.7148641 | 0.3832156 | 1.0642525 | 0.0005 |
| tCount | -0.1173087 | 0.3499090 | -0.3202261 | -0.7991742 | 0.5485687 | 0.7600 |
Table 39. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 969 | 8 | 2000 | 4 | 3200000 | 12144.5328521729s (~3.37 hours) | 1.03 | TRUE |
Movement
Table 40. Parameter descriptions.
| Parameter | Description |
|---|---|
bLength |
Coefficient for the effect of Length on logit(eMoved) |
bLengthSeason[i] |
Coefficient for the effect of the interaction between Length and Season on logit(eMoved) |
bMoved |
Intercept for logit(eMoved) |
bMovedSeason[i] |
Effect of ith season on logit(eMoved) |
eMoved[i] |
Probability of different site from previous encounter for ith recapture |
Length[i] |
Length of ith recaptured fish |
Moved[i] |
Indicates whether ith recapture is recorded at a different site from previous encounter |
nSeason |
Number of seasons in the study (2) |
Season[i] |
Season of ith recapture |
Bull Trout
Table 41. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | 0.0047745 | 0.0015523 | 3.0964570 | 0.0018221 | 0.0078775 | 0.0005 |
| bLengthSeason[2] | 0.0025145 | 0.0057703 | 0.5070124 | -0.0072400 | 0.0158471 | 0.6450 |
| bMoved | -1.9223766 | 0.6872842 | -2.7916148 | -3.3285555 | -0.6264036 | 0.0005 |
| bMovedSeason[2] | -0.2097086 | 2.4943308 | -0.1151158 | -5.5714534 | 4.3615303 | 0.9350 |
Table 42. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 139 | 4 | 2000 | 4 | 40000 | 3.592058 | 1.01 | TRUE |
Mountain Whitefish
Table 43. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | -0.0000585 | 0.0031176 | -0.0188312 | -0.0058705 | 0.0060392 | 0.9780 |
| bLengthSeason[2] | -0.0287949 | 0.0071939 | -4.0197767 | -0.0431402 | -0.0147266 | 0.0005 |
| bMoved | -0.0752615 | 0.7955858 | -0.0869078 | -1.6451885 | 1.4199044 | 0.9290 |
| bMovedSeason[2] | 6.0035221 | 1.7007025 | 3.5579101 | 2.7051475 | 9.2529943 | 0.0005 |
Table 44. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 455 | 4 | 2000 | 4 | 40000 | 11.02264 | 1.06 | TRUE |
Rainbow Trout
Table 45. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | 0.0066614 | 0.0066712 | 1.040321 | -0.0055244 | 0.0207671 | 0.300 |
| bLengthSeason[2] | 0.2206368 | 0.1230785 | 1.866868 | 0.0255527 | 0.4914047 | 0.005 |
| bMoved | -2.5320647 | 1.7059594 | -1.526541 | -6.1421186 | 0.5783143 | 0.105 |
| bMovedSeason[2] | -67.9724496 | 37.2760096 | -1.878494 | -149.6658038 | -8.7183550 | 0.004 |
Table 46. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 23 | 4 | 2000 | 4 | 40000 | 0.8048799 | 1.05 | TRUE |
Largescale Sucker
Table 47. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength | -0.0109916 | 0.0058396 | -1.881884 | -0.0228363 | 0.0008265 | 0.076 |
| bLengthSeason[2] | -0.2056773 | 0.0932733 | -2.182091 | -0.3865780 | -0.0231405 | 0.021 |
| bMoved | 4.5674208 | 2.5235068 | 1.810952 | -0.5522363 | 9.7472728 | 0.080 |
| bMovedSeason[2] | 90.1037990 | 41.0239003 | 2.178425 | 9.3551793 | 170.5578463 | 0.023 |
Table 48. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 70 | 4 | 2000 | 4 | 160000 | 5.18621802330017s | 1.06 | TRUE |
Observer Length Correction
Table 49. Parameter descriptions.
| Parameter | Description |
|---|---|
bLength[i] |
Relative inaccuracy of theith Observer |
ClassLength |
Mean Length of fish belonging to the ith class |
dClass[i] |
Prior value for the relative proportion of fish in the ith class |
eClass[i] |
Expected class of the ith fish |
eLength[i] |
Expected Length of the ith fish |
eSLength[i] |
Expected SD of the residual variation in Length for the ith |
Length[i] |
Observed fork length of the ith fish |
Observer[i] |
Observer of the ith fish where the first observer used a length board |
pClass[i] |
Proportion of fish in the ith class |
sLength[i] |
Relative imprecision of the ith Observer |
Bull Trout
Table 50. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength[2] | 0.8295510 | 0.0587294 | 14.767478 | 0.8250688 | 0.9812908 | 5e-04 |
| bLength[3] | 1.0905234 | 0.0751906 | 14.511789 | 0.9446459 | 1.2353038 | 5e-04 |
| bLength[4] | 0.9982138 | 0.0392980 | 25.985577 | 0.9532832 | 1.0926534 | 5e-04 |
| bLength[5] | 0.8487111 | 0.0367764 | 23.255621 | 0.7921152 | 0.9433502 | 5e-04 |
| bLength[6] | 0.9921179 | 0.0493985 | 19.583259 | 0.8439292 | 0.9969706 | 5e-04 |
| bLength[7] | 0.9605280 | 0.0759563 | 13.000224 | 0.9103218 | 1.0903138 | 5e-04 |
| bLength[8] | 1.0169095 | 0.0537331 | 18.958199 | 0.9108885 | 1.1173630 | 5e-04 |
| sLength[2] | 1.0413350 | 1.2949400 | 1.160473 | 1.0013062 | 5.2950826 | 5e-04 |
| sLength[3] | 6.3852291 | 4.9522513 | 1.507112 | 1.3925108 | 20.0853509 | 5e-04 |
| sLength[4] | 1.3653024 | 2.2831090 | 1.104397 | 1.0024408 | 8.7580734 | 5e-04 |
| sLength[5] | 3.0746659 | 2.8720854 | 1.389820 | 1.0322016 | 11.2835228 | 5e-04 |
| sLength[6] | 1.0300262 | 1.3582406 | 1.177558 | 1.0009804 | 6.1623492 | 5e-04 |
| sLength[7] | 1.1668169 | 1.1535121 | 1.268215 | 1.0072669 | 5.1107757 | 5e-04 |
| sLength[8] | 7.0935713 | 4.7057892 | 1.667923 | 1.3398539 | 18.7089936 | 5e-04 |
Table 51. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1058 | 14 | 2000 | 4 | 5120000 | 21891.7364845276s (~6.08 hours) | 1.41 | FALSE |
Mountain Whitefish
Table 52. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength[2] | 0.9239473 | 0.0075053 | 123.112458 | 0.9094790 | 0.9367955 | 5e-04 |
| bLength[3] | 0.9137584 | 0.0156839 | 58.256684 | 0.8823468 | 0.9442200 | 5e-04 |
| bLength[4] | 1.0083762 | 0.0091092 | 110.700216 | 0.9903784 | 1.0265663 | 5e-04 |
| bLength[5] | 0.9307453 | 0.0049084 | 189.551196 | 0.9200066 | 0.9388649 | 5e-04 |
| bLength[6] | 0.7627435 | 0.0051445 | 148.271709 | 0.7526195 | 0.7728329 | 5e-04 |
| bLength[7] | 0.9784577 | 0.0101676 | 96.252021 | 0.9584882 | 0.9978365 | 5e-04 |
| bLength[8] | 0.8497020 | 0.0157436 | 53.981561 | 0.8188708 | 0.8812846 | 5e-04 |
| sLength[2] | 2.6767563 | 0.6596459 | 3.751118 | 1.1847571 | 3.3681802 | 5e-04 |
| sLength[3] | 4.5891462 | 0.8363494 | 5.472418 | 2.9277363 | 6.2051080 | 5e-04 |
| sLength[4] | 4.0824229 | 0.4050702 | 10.099657 | 3.3107849 | 4.9000491 | 5e-04 |
| sLength[5] | 1.2634793 | 0.1900469 | 6.849920 | 1.0532771 | 1.8038236 | 5e-04 |
| sLength[6] | 3.2271668 | 0.1891921 | 17.059692 | 2.8691190 | 3.6185026 | 5e-04 |
| sLength[7] | 4.1329454 | 0.3829660 | 10.791872 | 3.3782864 | 4.8733304 | 5e-04 |
| sLength[8] | 6.6058955 | 0.6543448 | 10.092474 | 5.3297159 | 7.8958873 | 5e-04 |
Table 53. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 7463 | 14 | 2000 | 4 | 160000 | 2951.50112128258s (~49.19 minutes) | 1.06 | TRUE |
Suckers
Table 54. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bLength[2] | 0.8200547 | 0.0122134 | 67.116151 | 0.7950339 | 0.8428677 | 5e-04 |
| bLength[3] | 1.1119342 | 0.0325977 | 34.105340 | 1.0449897 | 1.1773771 | 5e-04 |
| bLength[4] | 0.9507303 | 0.0057486 | 165.448619 | 0.9410518 | 0.9622337 | 5e-04 |
| bLength[5] | 0.9018186 | 0.0017900 | 503.802139 | 0.8982251 | 0.9052863 | 5e-04 |
| bLength[6] | 0.7499056 | 0.0058935 | 127.245130 | 0.7382510 | 0.7614752 | 5e-04 |
| bLength[7] | 0.9224197 | 0.0113655 | 81.178089 | 0.9000950 | 0.9452503 | 5e-04 |
| bLength[8] | 0.7085999 | 0.0188290 | 37.631013 | 0.6721234 | 0.7456156 | 5e-04 |
| sLength[2] | 5.0507029 | 1.0358079 | 4.899389 | 3.0787038 | 7.1386204 | 5e-04 |
| sLength[3] | 9.0276187 | 2.3308736 | 3.970438 | 5.3509156 | 14.3878126 | 5e-04 |
| sLength[4] | 2.9661280 | 1.0638723 | 2.607776 | 1.0468088 | 4.5527721 | 5e-04 |
| sLength[5] | 1.0212649 | 0.0299129 | 34.440664 | 1.0008292 | 1.1084714 | 5e-04 |
| sLength[6] | 5.4572978 | 0.4315599 | 12.648395 | 4.6128940 | 6.2992004 | 5e-04 |
| sLength[7] | 6.4705785 | 0.7831361 | 8.259786 | 4.9504104 | 8.0090055 | 5e-04 |
| sLength[8] | 12.3621281 | 0.9936523 | 12.474686 | 10.5690973 | 14.4383197 | 5e-04 |
Table 55. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 3467 | 14 | 2000 | 4 | 40000 | 324.3198 | 1.02 | TRUE |
Abundance
Table 56. Parameter descriptions.
| Parameter | Description |
|---|---|
bDensitySeason[i] |
Effect of ith Season on bDensity |
bDensitySite[i] |
Random effect of ith Site on bDensity |
bDensitySiteYear[i, j] |
Effect of ith Site in jth year on bDensity |
bDensityYear[i] |
Random effect of ith Year on bDensity |
bDistribution |
Intercept for eDistribution |
bDistributionRegime[i] |
Effect of ith Regime on bDistribution |
bDistributionSeason[i] |
Effect of ith Season on bDistribution |
bDistributionYear[i] |
Random effect of ith Year on bDistribution |
bEfficiency |
Intercept for logit(eEfficiency) |
bEfficiencySessionSeasonYear[i, j, k] |
Effect of ith Session in jth Season of kth Year on bEfficiency |
bRate |
Baseline rate of change (relative to the previous year) in eDensity due to year effect |
bRateRegime[i] |
Deviate from bRate due to regime effect in the ith year |
bRateYear[i] |
Random deviate from bRate due to year effect in the ith year |
Catch[i] |
Number of fish caught on ith site visit |
eAbundance[i] |
Predicted abundance on ith site visit |
eDensity[i] |
Predicted lineal density on ith site visit |
eDistribution[i] |
Predicted relationship between centred river kilometre and ith site visit on bDensity |
eEfficiency[i] |
Predicted efficiency during ith site visit |
eRateYear[i] |
Rate of change in year effect between the (i-1)th and ith year |
Marked[i] |
Number of marked fish caught in ith river visit |
sRateYear |
SD of the distribution of bRateYear |
Tagged[i] |
Number of fish tagged prior to ith river visit |
Bull Trout
Juvenile
Table 57. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | 0.2533460 | 0.3526480 | 0.7075806 | -0.4234096 | 0.9637902 | 0.4750 |
| bDistribution | -0.0233601 | 0.0693394 | -0.3429197 | -0.1703516 | 0.1155390 | 0.7310 |
| bDistributionRegime[2] | 0.0178055 | 0.0495882 | 0.3369297 | -0.0878477 | 0.1129369 | 0.6890 |
| bDistributionSeason[2] | -0.0053668 | 0.0330636 | -0.1497046 | -0.0673432 | 0.0603336 | 0.8880 |
| bEfficiency | -3.1456925 | 0.1503743 | -20.9322654 | -3.4414052 | -2.8628312 | 0.0005 |
| bEfficiencySeason[2] | -0.3680849 | 0.3521946 | -1.0626181 | -1.0710439 | 0.3097583 | 0.2830 |
| bMultiplierType[2] | 0.0061974 | 0.2486555 | 0.0647286 | -0.4353917 | 0.5237342 | 0.9850 |
| bRate | 0.2398310 | 0.1246984 | 1.9257873 | -0.0254257 | 0.4808559 | 0.0750 |
| bRateRegime[2] | -0.2953578 | 0.2231386 | -1.3395355 | -0.7454213 | 0.1305092 | 0.1640 |
| sDensitySite | 0.6256241 | 0.1618852 | 4.0192569 | 0.4141142 | 1.0325745 | 0.0005 |
| sDensitySiteYear | 0.1821771 | 0.0685620 | 2.5884171 | 0.0437079 | 0.3051739 | 0.0005 |
| sDispersion | -0.9557252 | 0.1600824 | -6.0504939 | -1.3264700 | -0.6976038 | 0.0005 |
| sDispersionType[2] | 1.1719990 | 0.2645835 | 4.4419450 | 0.6591284 | 1.7018247 | 0.0005 |
| sDistributionYear | 0.0588833 | 0.0377955 | 1.6893004 | 0.0066366 | 0.1534442 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.2616722 | 0.0546470 | 4.8175419 | 0.1614897 | 0.3780271 | 0.0005 |
| sRateYear | 0.3999705 | 0.1237228 | 3.3837426 | 0.2380854 | 0.7120449 | 0.0005 |
| tAbundance | -0.2953578 | 0.2231386 | -1.3395355 | -0.7454213 | 0.1305092 | 0.1640 |
| tDistribution | 0.0178055 | 0.0495882 | 0.3369297 | -0.0878477 | 0.1129369 | 0.6890 |
Table 58. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1044 | 18 | 2000 | 4 | 320000 | 2270.38351392746s (~37.84 minutes) | 1.09 | TRUE |
Adult
Table 59. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -0.2882166 | 0.3631732 | -0.6931211 | -0.8930392 | 0.5449565 | 0.4590 |
| bDistribution | 0.0582116 | 0.0477049 | 1.2135668 | -0.0404665 | 0.1443064 | 0.2350 |
| bDistributionRegime[2] | 0.0426375 | 0.0378211 | 1.1245778 | -0.0355627 | 0.1151198 | 0.2390 |
| bDistributionSeason[2] | 0.1345567 | 0.0300632 | 4.4722849 | 0.0744979 | 0.1923452 | 0.0005 |
| bEfficiency | -3.6436894 | 0.1175444 | -30.9586278 | -3.8615137 | -3.4078391 | 0.0005 |
| bEfficiencySeason[2] | -0.0278121 | 0.3601965 | -0.1923717 | -0.8859242 | 0.5592198 | 0.9160 |
| bMultiplierType[2] | 0.6207753 | 0.1884473 | 3.2836396 | 0.2474707 | 0.9902832 | 0.0020 |
| bRate | 0.0392847 | 0.0362042 | 1.1615108 | -0.0235794 | 0.1210203 | 0.1890 |
| bRateRegime[2] | -0.0852672 | 0.0874156 | -1.0154568 | -0.2865160 | 0.0750505 | 0.2730 |
| sDensitySite | 0.4525169 | 0.1191209 | 3.9748294 | 0.2944337 | 0.7601694 | 0.0005 |
| sDensitySiteYear | 0.4107809 | 0.0443360 | 9.2956743 | 0.3260812 | 0.5028637 | 0.0005 |
| sDispersion | -0.9387993 | 0.1042657 | -9.0556224 | -1.1721705 | -0.7530630 | 0.0005 |
| sDispersionType[2] | 0.7603995 | 0.1914199 | 3.9530481 | 0.3746911 | 1.1162625 | 0.0005 |
| sDistributionYear | 0.0287660 | 0.0208965 | 1.5181003 | 0.0021586 | 0.0780286 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.2291219 | 0.0415293 | 5.5300904 | 0.1532975 | 0.3167081 | 0.0005 |
| sRateYear | 0.1318066 | 0.0768006 | 1.8128623 | 0.0181214 | 0.3089119 | 0.0005 |
| tAbundance | -0.0852672 | 0.0874156 | -1.0154568 | -0.2865160 | 0.0750505 | 0.2730 |
| tDistribution | 0.0426375 | 0.0378211 | 1.1245778 | -0.0355627 | 0.1151198 | 0.2390 |
Table 60. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1044 | 18 | 2000 | 4 | 40000 | 466.533728837967s (~7.78 minutes) | 1.1 | TRUE |
Mountain Whitefish
Juvenile
Table 61. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | 0.4862685 | 0.6922579 | 0.7001886 | -0.8450878 | 1.8823028 | 0.4790 |
| bDistribution | 0.0925140 | 0.1035882 | 0.8815221 | -0.1046683 | 0.2989867 | 0.3840 |
| bDistributionRegime[2] | 0.0592829 | 0.0767315 | 0.7893818 | -0.0827539 | 0.2188564 | 0.3820 |
| bDistributionSeason[2] | -0.0927744 | 0.0346993 | -2.6870507 | -0.1619466 | -0.0267106 | 0.0080 |
| bEfficiency | -5.6909935 | 0.4475851 | -12.7940782 | -6.6846042 | -4.9461266 | 0.0005 |
| bEfficiencySeason[2] | 0.0854189 | 0.6929100 | 0.1075346 | -1.3297729 | 1.4144776 | 0.9040 |
| bMultiplierType[2] | 0.3644342 | 0.2513478 | 1.4489947 | -0.1430174 | 0.8561175 | 0.1580 |
| bRate | 0.1757425 | 0.3396964 | 0.6057143 | -0.3796173 | 0.9408574 | 0.5570 |
| bRateRegime[2] | -0.2949386 | 0.5903909 | -0.5254461 | -1.5057016 | 0.8348206 | 0.5500 |
| sDensitySite | 0.8849467 | 0.2266866 | 4.0854721 | 0.5899266 | 1.4592510 | 0.0005 |
| sDensitySiteYear | 0.4996290 | 0.0693170 | 7.2209988 | 0.3684122 | 0.6423932 | 0.0005 |
| sDispersion | -0.6196515 | 0.0922471 | -6.7298350 | -0.8058056 | -0.4495254 | 0.0005 |
| sDispersionType[2] | 0.9069275 | 0.1816135 | 5.0131306 | 0.5538005 | 1.2843566 | 0.0005 |
| sDistributionYear | 0.0804613 | 0.0441286 | 1.9433969 | 0.0110435 | 0.1903641 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.2879750 | 0.0658752 | 4.4281369 | 0.1658714 | 0.4345835 | 0.0005 |
| sRateYear | 0.6751302 | 0.3704022 | 2.0605684 | 0.3271509 | 1.8223557 | 0.0005 |
| tAbundance | -0.2949386 | 0.5903909 | -0.5254461 | -1.5057016 | 0.8348206 | 0.5500 |
| tDistribution | 0.0592829 | 0.0767315 | 0.7893818 | -0.0827539 | 0.2188564 | 0.3820 |
Table 62. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 815 | 18 | 2000 | 4 | 1280000 | 6681.29352998734s (~1.86 hours) | 1.06 | TRUE |
Adult
Table 63. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensitySeason[2] | -0.6868749 | 0.1226750 | -5.5925381 | -0.9343428 | -0.4451391 | 0.0005 |
| bDistribution | 0.0886822 | 0.0526896 | 1.7049560 | -0.0126144 | 0.1913519 | 0.0920 |
| bDistributionRegime[2] | 0.0420695 | 0.0409475 | 1.0423150 | -0.0381254 | 0.1265885 | 0.2620 |
| bDistributionSeason[2] | -0.0634293 | 0.0196418 | -3.2163562 | -0.1015703 | -0.0241077 | 0.0010 |
| bEfficiency | -4.0053718 | 0.0658635 | -60.7929739 | -4.1304451 | -3.8727384 | 0.0005 |
| bEfficiencySeason[2] | 0.8860861 | 0.1256474 | 7.0727832 | 0.6472767 | 1.1345090 | 0.0005 |
| bMultiplierType[2] | 0.4903411 | 0.1899299 | 2.5879390 | 0.1368843 | 0.8875594 | 0.0090 |
| bRate | 0.0063572 | 0.0489622 | 0.2945439 | -0.0605749 | 0.1407975 | 0.8480 |
| bRateRegime[2] | -0.0217268 | 0.0831710 | -0.3367701 | -0.2258688 | 0.1238516 | 0.7370 |
| sDensitySite | 0.4817200 | 0.1199897 | 4.2086238 | 0.3275907 | 0.8043769 | 0.0005 |
| sDensitySiteYear | 0.3702445 | 0.0305688 | 12.1085225 | 0.3107628 | 0.4295677 | 0.0005 |
| sDispersion | -0.8187999 | 0.0387121 | -21.1373592 | -0.8964936 | -0.7413720 | 0.0005 |
| sDispersionType[2] | 0.9273884 | 0.1211654 | 7.6386926 | 0.6788134 | 1.1644392 | 0.0005 |
| sDistributionYear | 0.0517590 | 0.0228657 | 2.3285342 | 0.0115348 | 0.1005678 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.2546918 | 0.0347120 | 7.3610053 | 0.1916124 | 0.3307661 | 0.0005 |
| sRateYear | 0.0894262 | 0.0724479 | 1.4062163 | 0.0040934 | 0.2791827 | 0.0005 |
| tAbundance | -0.0217268 | 0.0831710 | -0.3367701 | -0.2258688 | 0.1238516 | 0.7370 |
| tDistribution | 0.0420695 | 0.0409475 | 1.0423150 | -0.0381254 | 0.1265885 | 0.2620 |
Table 64. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1044 | 18 | 2000 | 4 | 1280000 | 7749.5605905056s (~2.15 hours) | 1.1 | TRUE |
Rainbow Trout
Adult
Table 65. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 0.6533293 | 0.4609334 | 1.3877529 | -0.3073958 | 1.5434404 | 0.1640 |
| bDensitySeason[2] | 0.1720165 | 0.6778927 | 0.3018074 | -1.0095224 | 1.6585467 | 0.7950 |
| bEfficiency | -2.6346217 | 0.2949553 | -8.9435060 | -3.2258291 | -2.0674508 | 0.0005 |
| bEfficiencySeason[2] | -0.3641696 | 0.6892913 | -0.6109407 | -1.8874158 | 0.8291461 | 0.5550 |
| sDensitySite | 1.1591075 | 0.3454002 | 3.5174602 | 0.7154463 | 2.0348782 | 0.0005 |
| sDensitySiteYear | 0.4936966 | 0.1503454 | 3.2774872 | 0.1919907 | 0.7889074 | 0.0005 |
| sDensityYear | 0.2497891 | 0.1971106 | 1.4120786 | 0.0174696 | 0.7465993 | 0.0005 |
| sDispersion | -1.2339171 | 0.9378023 | -1.5792869 | -4.1051578 | -0.3330295 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.3143309 | 0.1553879 | 1.9702533 | 0.0124534 | 0.6138537 | 0.0005 |
Table 66. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 740 | 9 | 2000 | 4 | 320000 | 467.732274055481s (~7.8 minutes) | 1.04 | TRUE |
Largescale Sucker
Adult
Table 67. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | 5.2807106 | 0.2670364 | 19.7358861 | 4.7371381 | 5.7875626 | 0.0005 |
| bDensitySeason[2] | 0.0043752 | 0.5339726 | 0.0447323 | -0.9464182 | 1.1476755 | 0.9910 |
| bEfficiency | -3.3755875 | 0.1625481 | -20.7593640 | -3.6988653 | -3.0548126 | 0.0005 |
| bEfficiencySeason[2] | -1.2491326 | 0.5488653 | -2.2899028 | -2.3936702 | -0.2555397 | 0.0110 |
| sDensitySite | 0.4422012 | 0.1264301 | 3.6323013 | 0.2578177 | 0.7503333 | 0.0005 |
| sDensitySiteYear | 0.4872211 | 0.0648153 | 7.5507728 | 0.3678700 | 0.6237233 | 0.0005 |
| sDensityYear | 0.4375645 | 0.2431456 | 2.0125583 | 0.1675406 | 1.0840311 | 0.0005 |
| sDispersion | -0.5288058 | 0.0618686 | -8.5826487 | -0.6594010 | -0.4103021 | 0.0005 |
| sEfficiencySessionSeasonYear | 0.5601213 | 0.0860905 | 6.6103831 | 0.4176117 | 0.7566112 | 0.0005 |
Table 68. Model summary.
| n | K | nsamples | nchains | nsims | duration | rhat | converged |
|---|---|---|---|---|---|---|---|
| 600 | 9 | 2000 | 4 | 320000 | 398.652538061142s (~6.64 minutes) | 1.03 | TRUE |
Figures
Growth
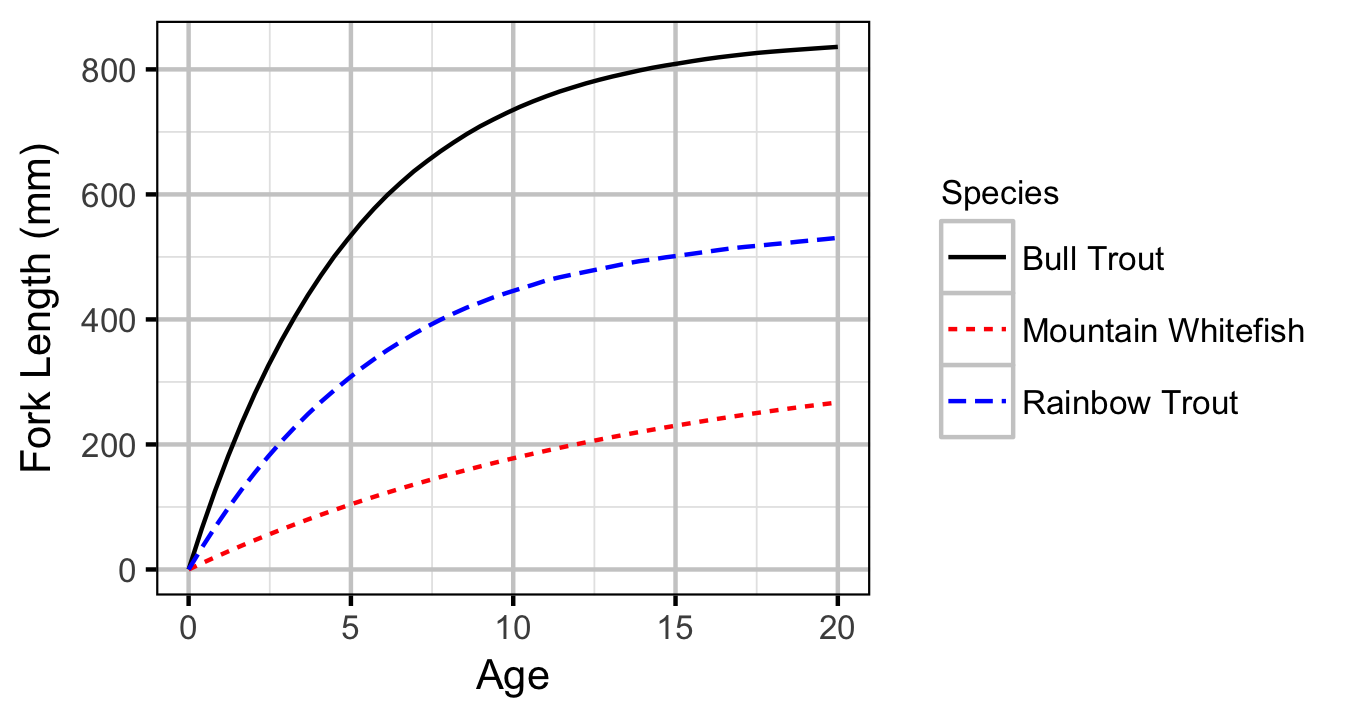
Bull Trout
Mountain Whitefish
Rainbow Trout
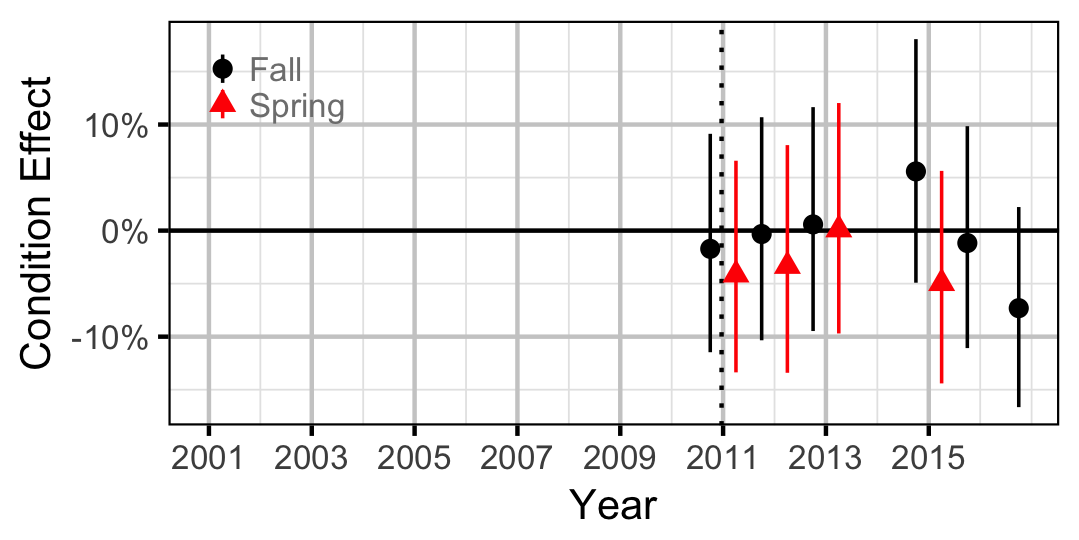
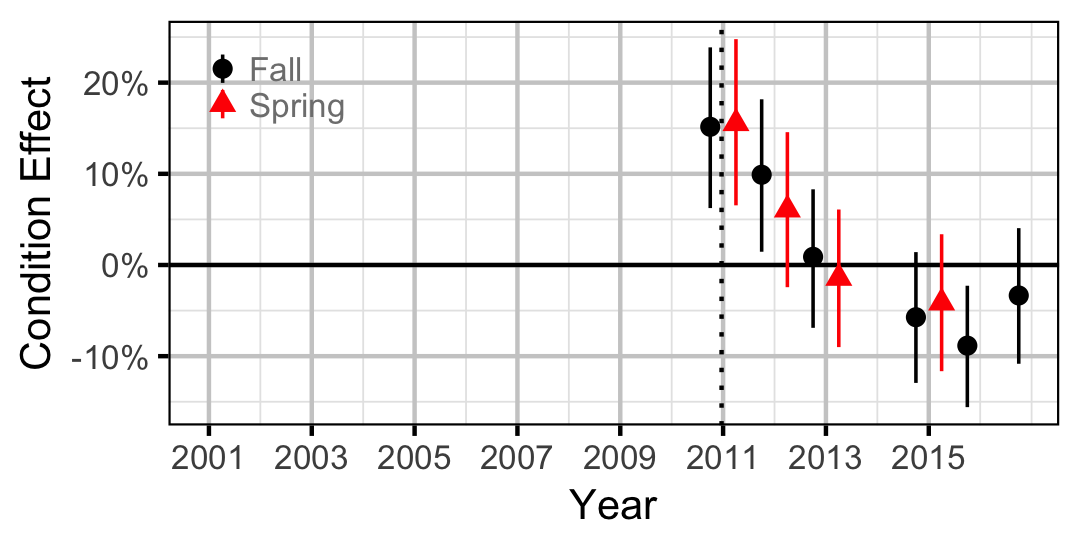
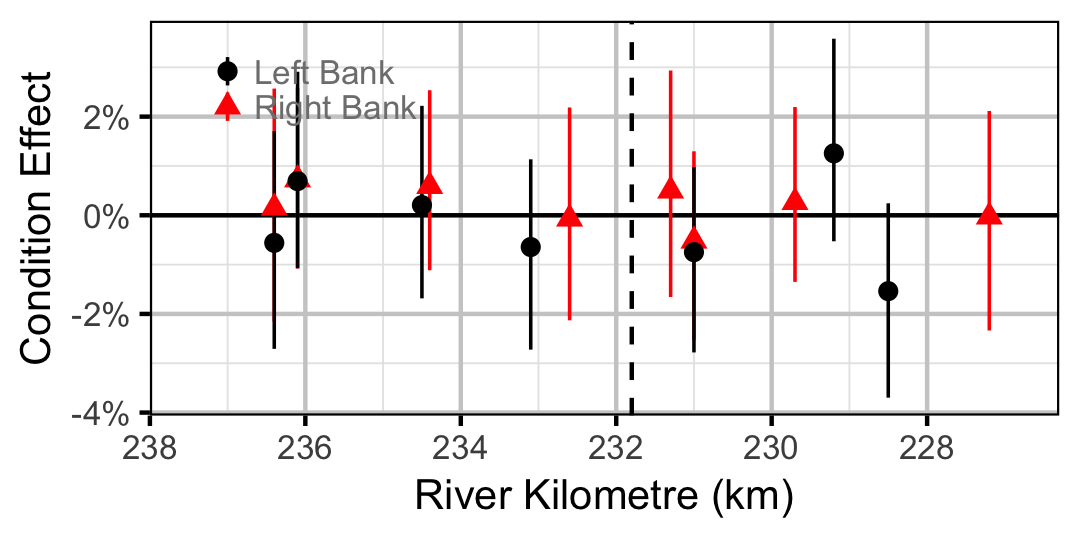
Condition
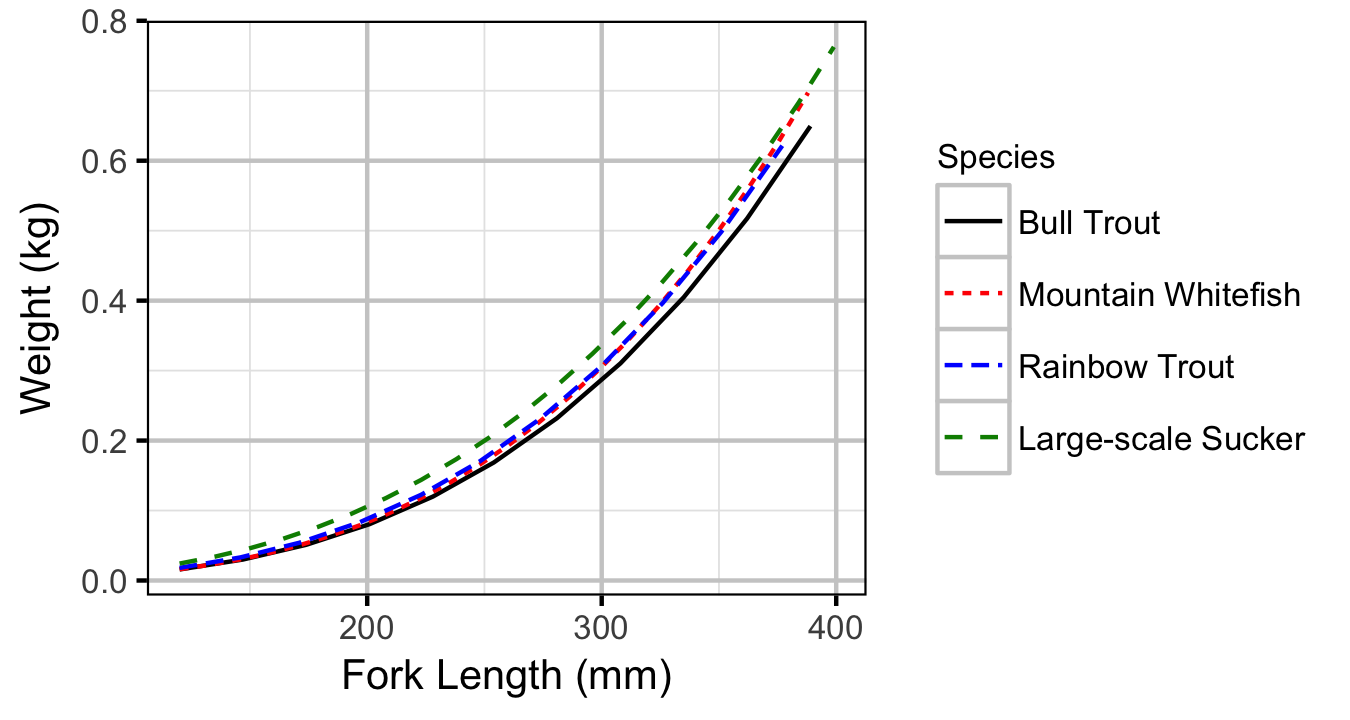
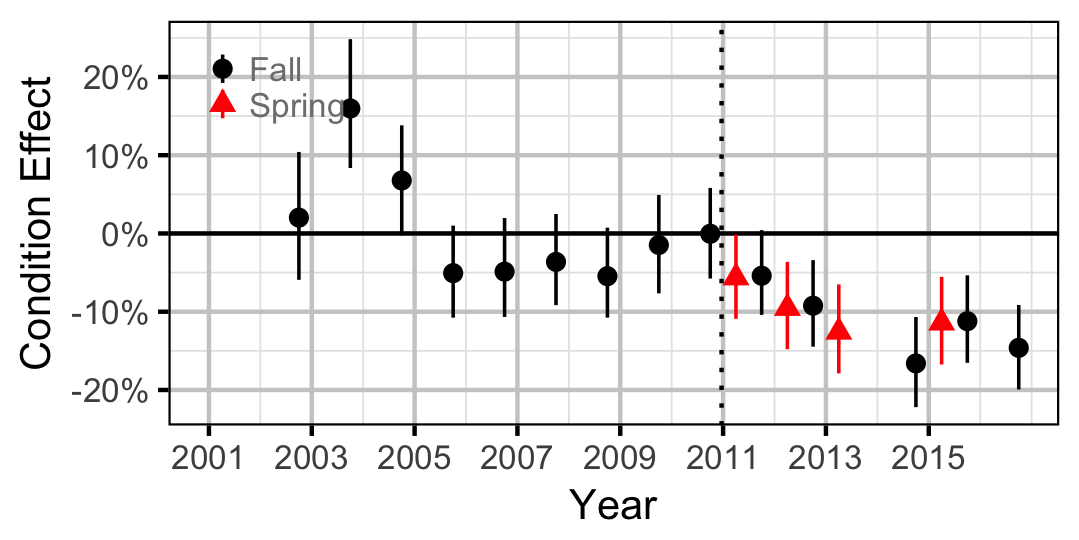
Bull Trout
Juvenile
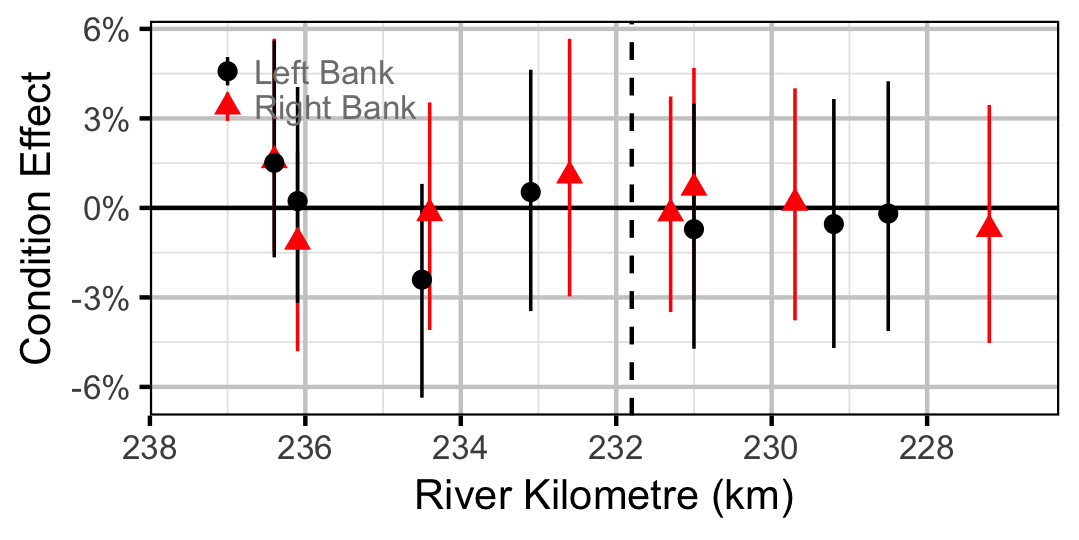
Adult
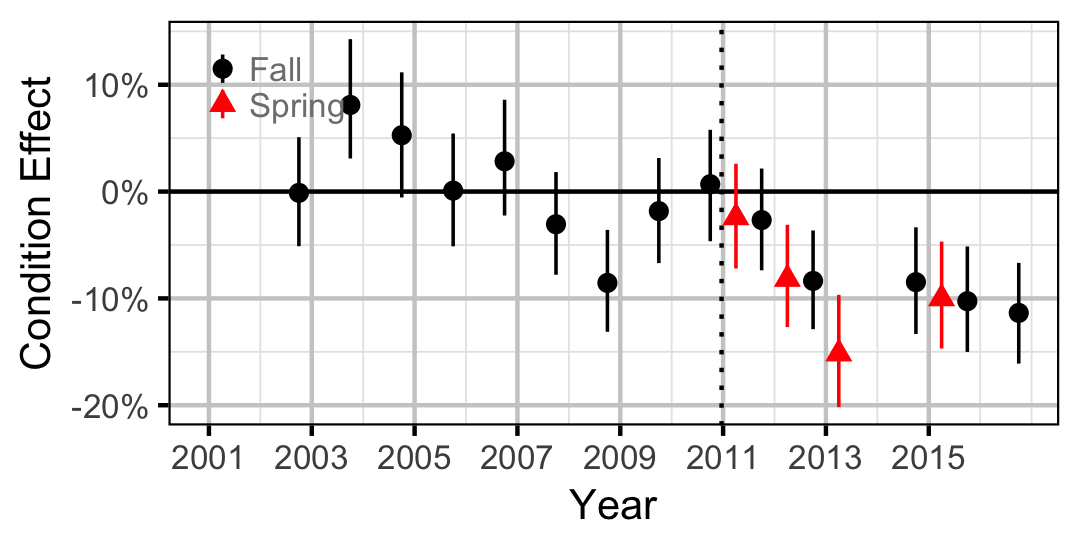
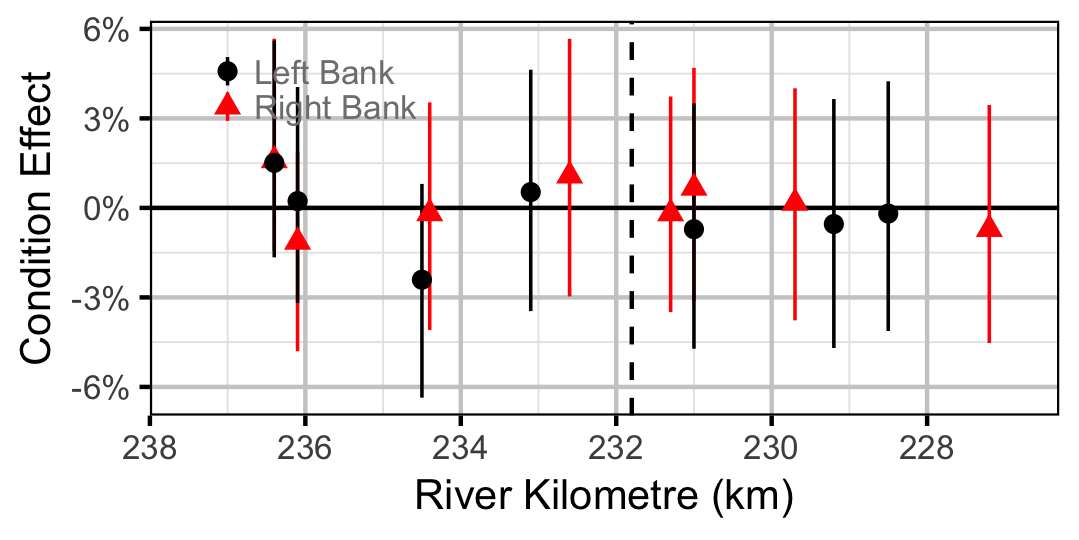
Mountain Whitefish
Juvenile
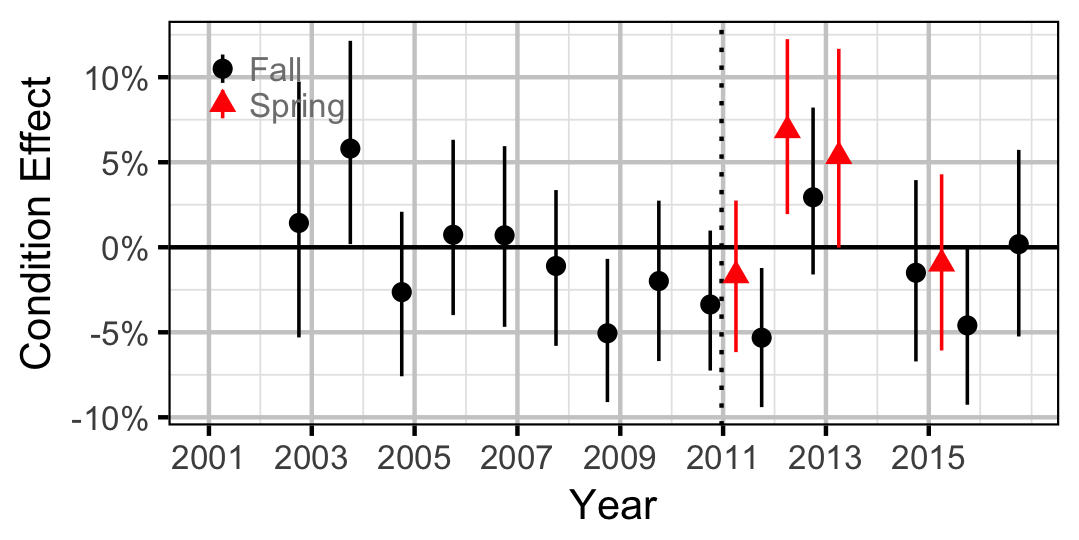
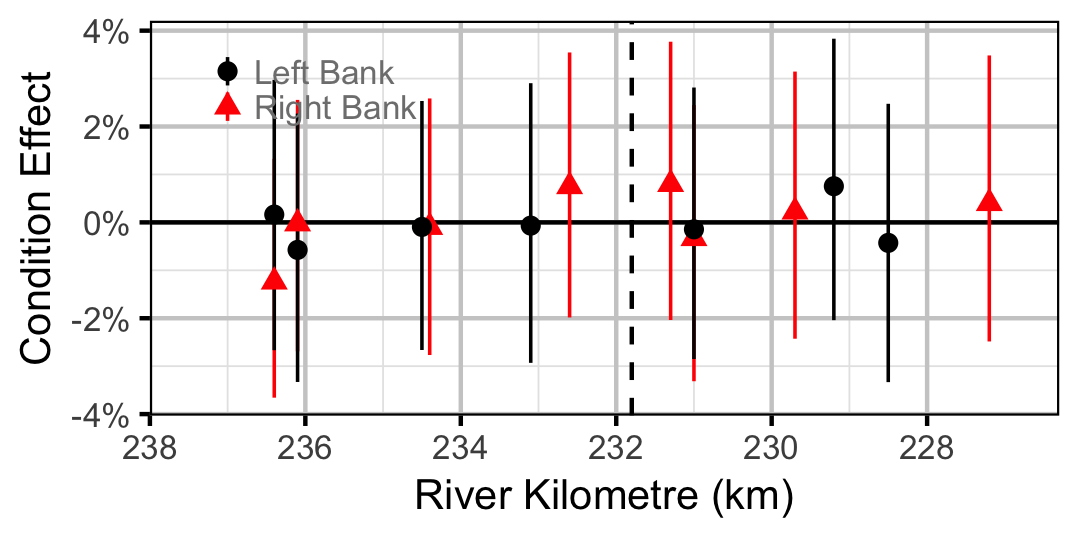
Adult
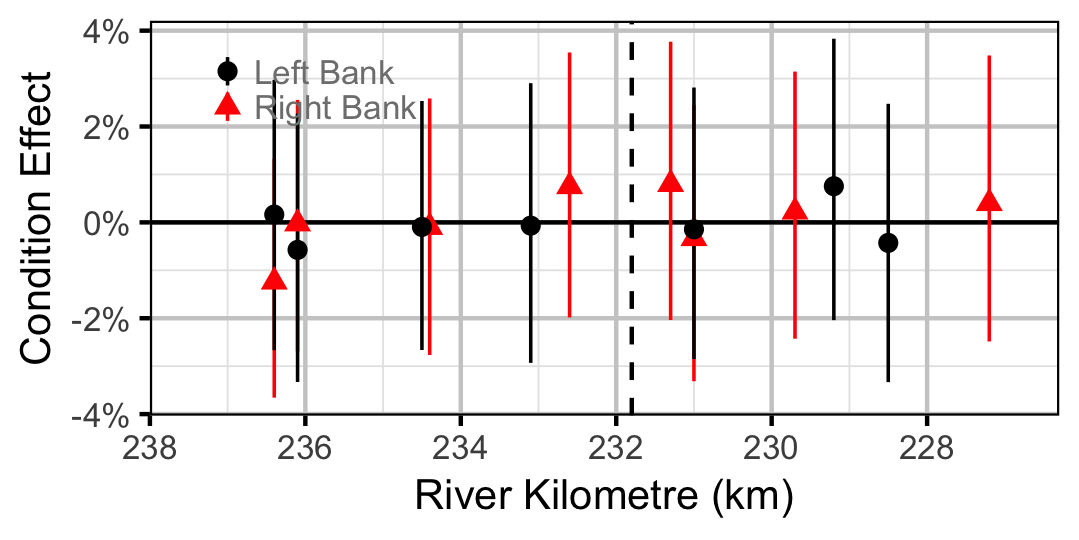
Rainbow Trout
Juvenile
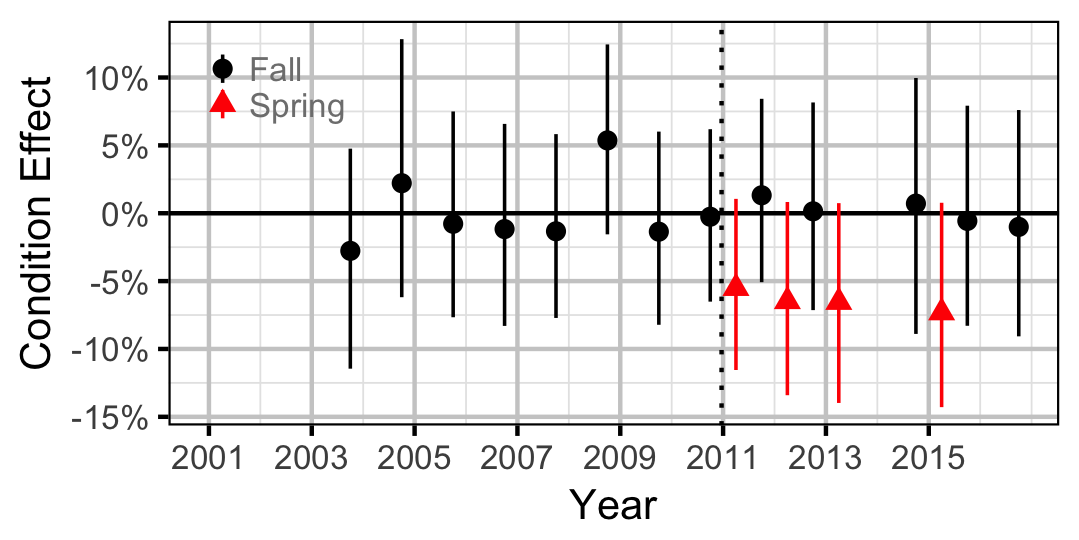
Adult
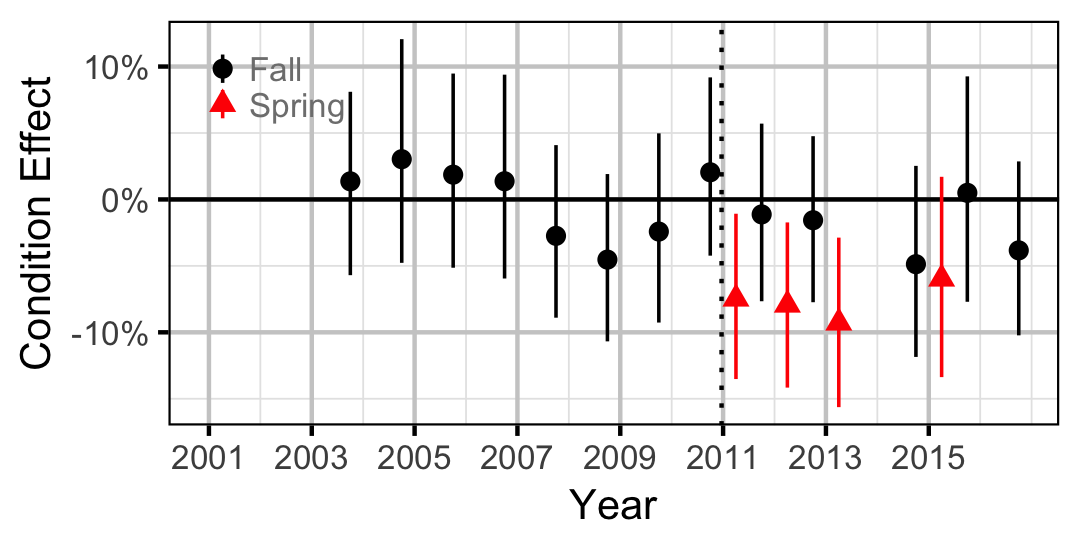
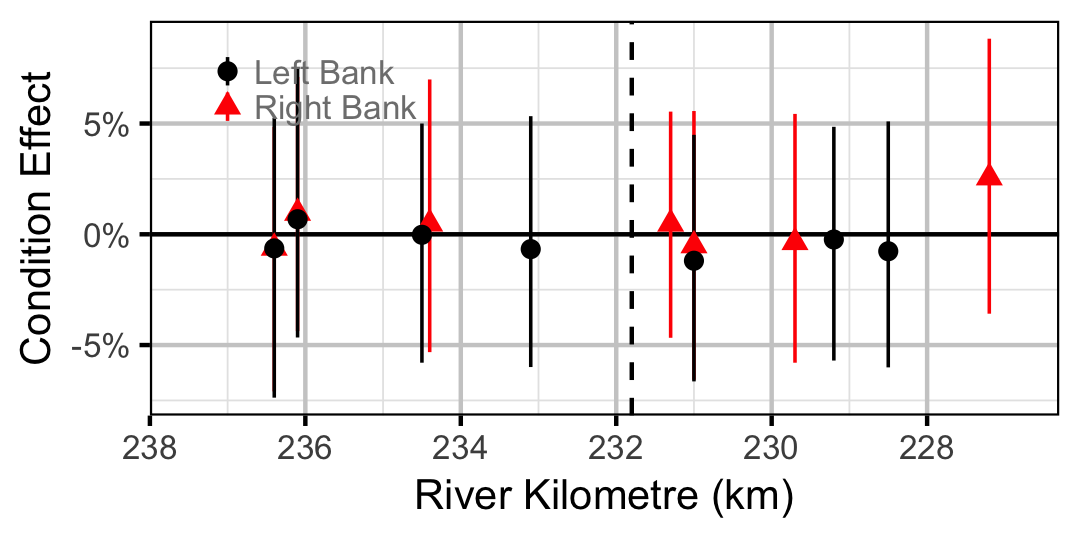
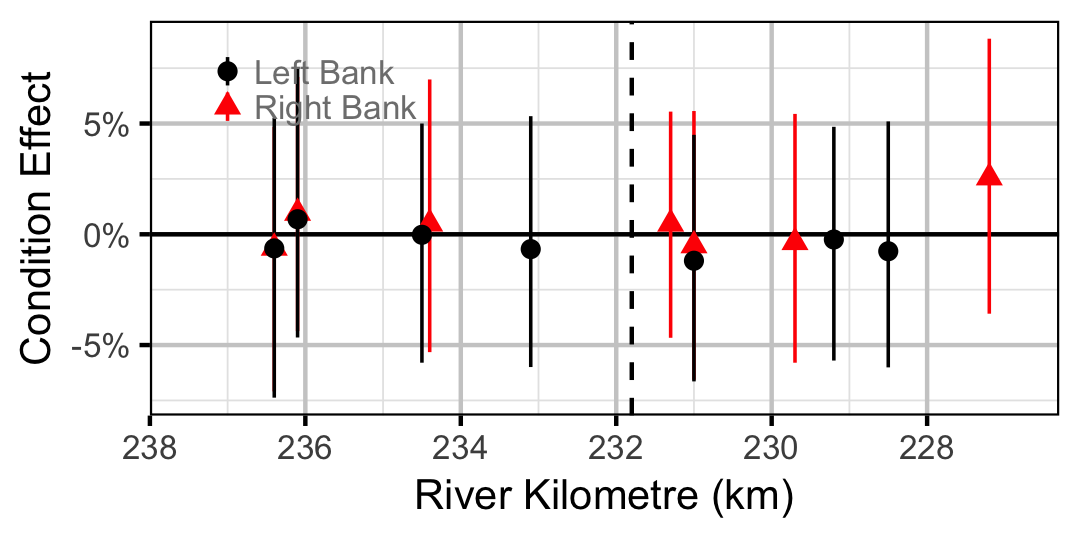
Largescale Sucker
Juvenile
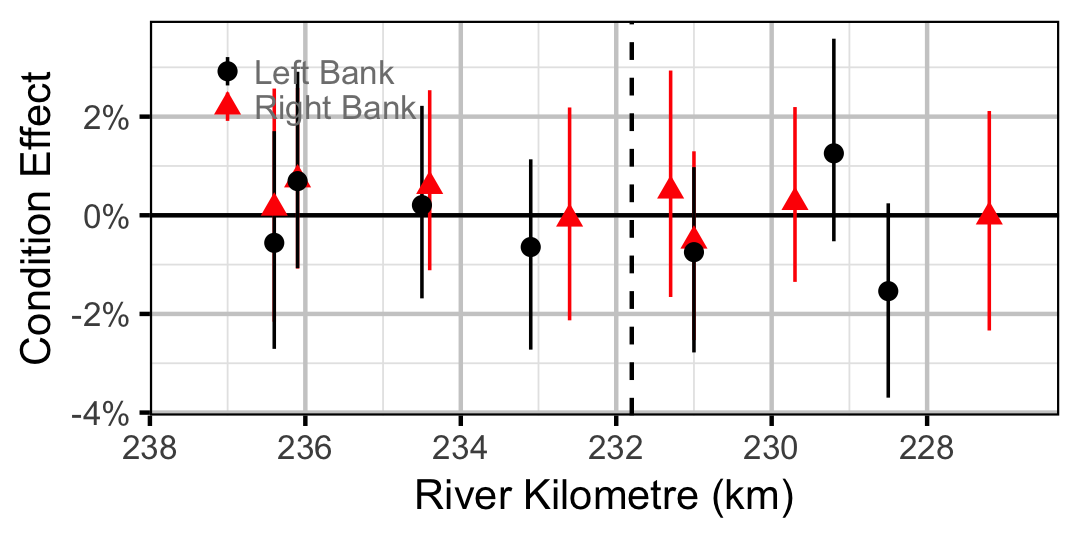
Adult
Occupancy
Rainbow Trout
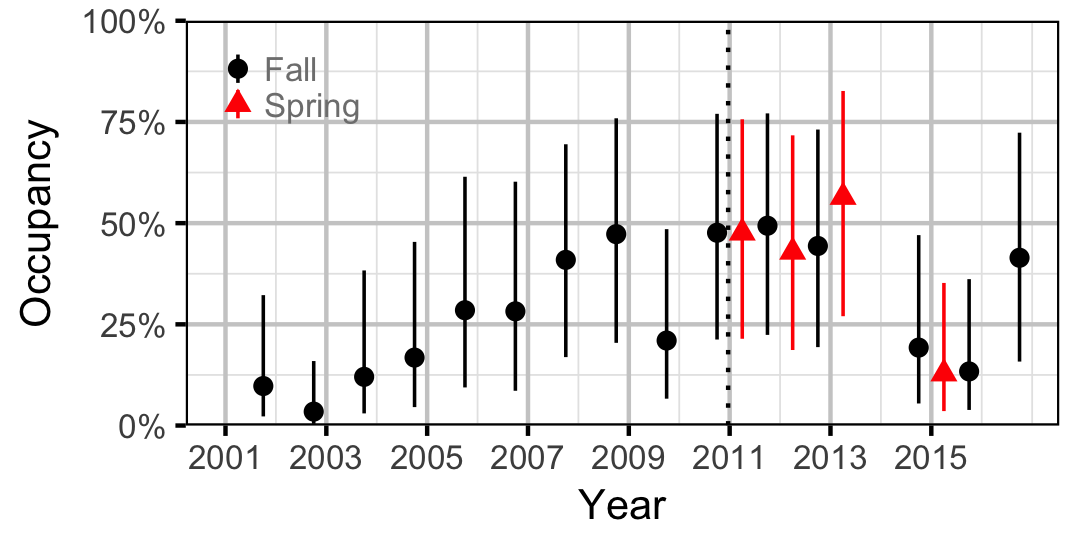
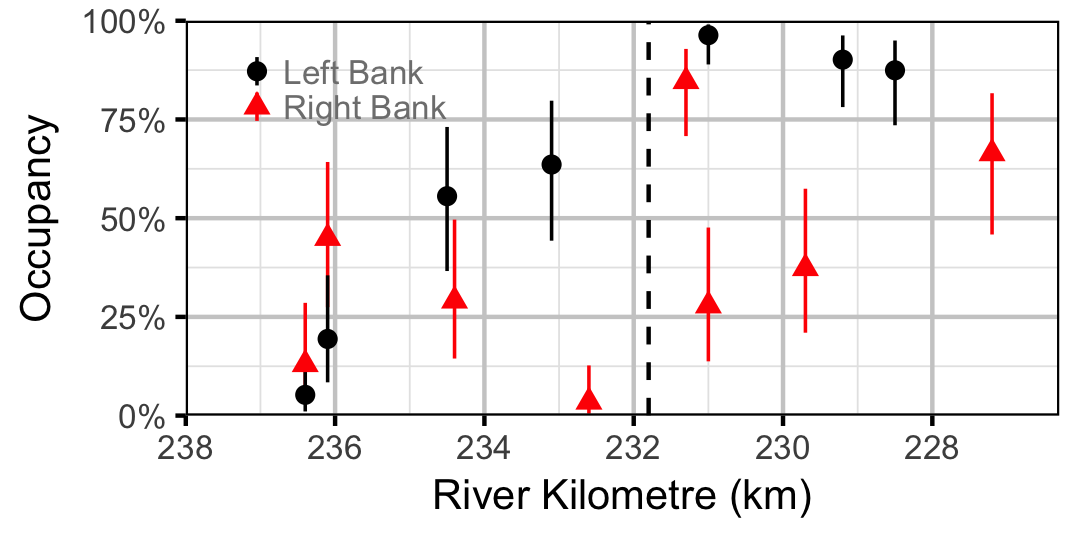
Burbot
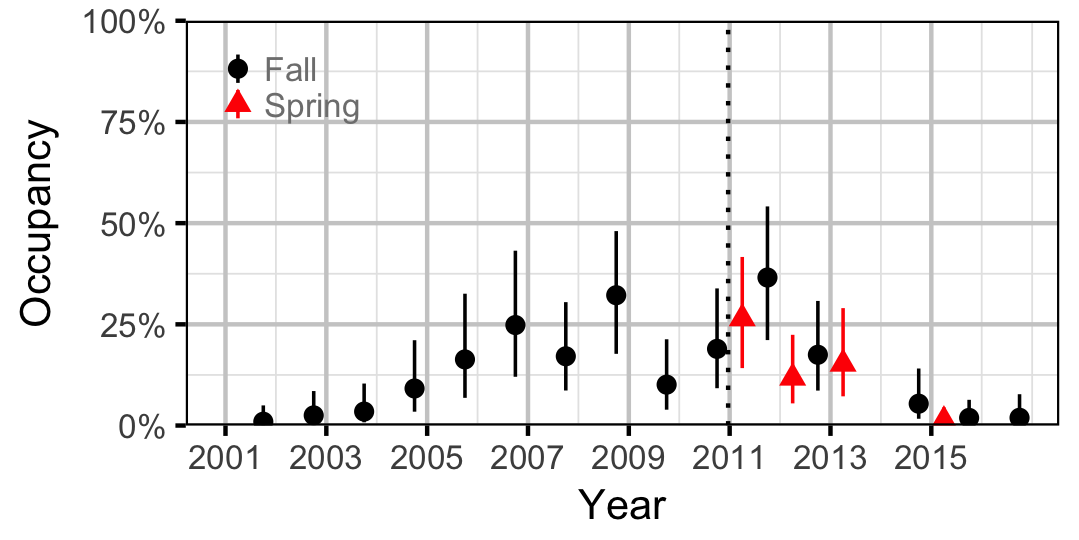
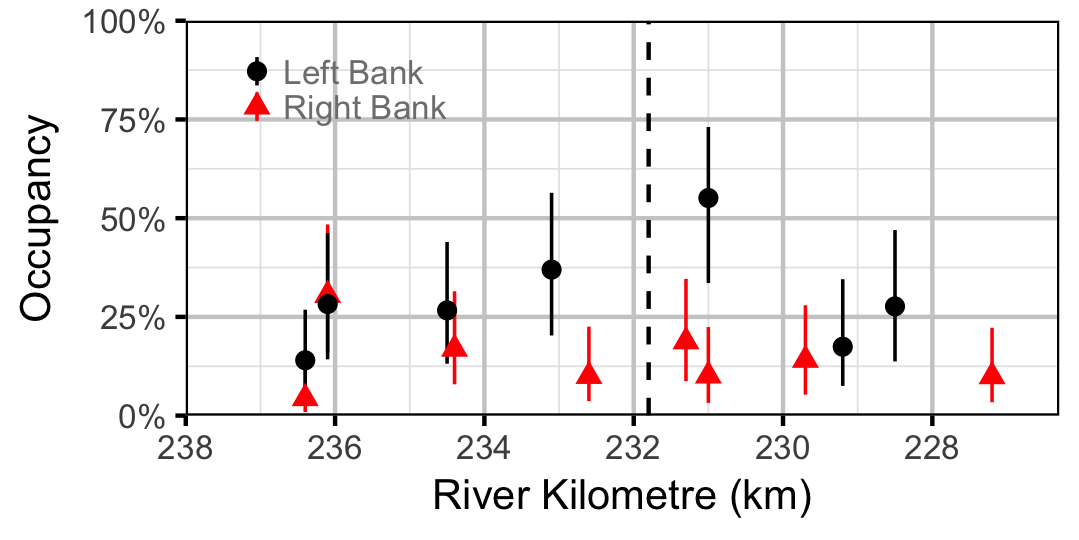
Lake Whitefish
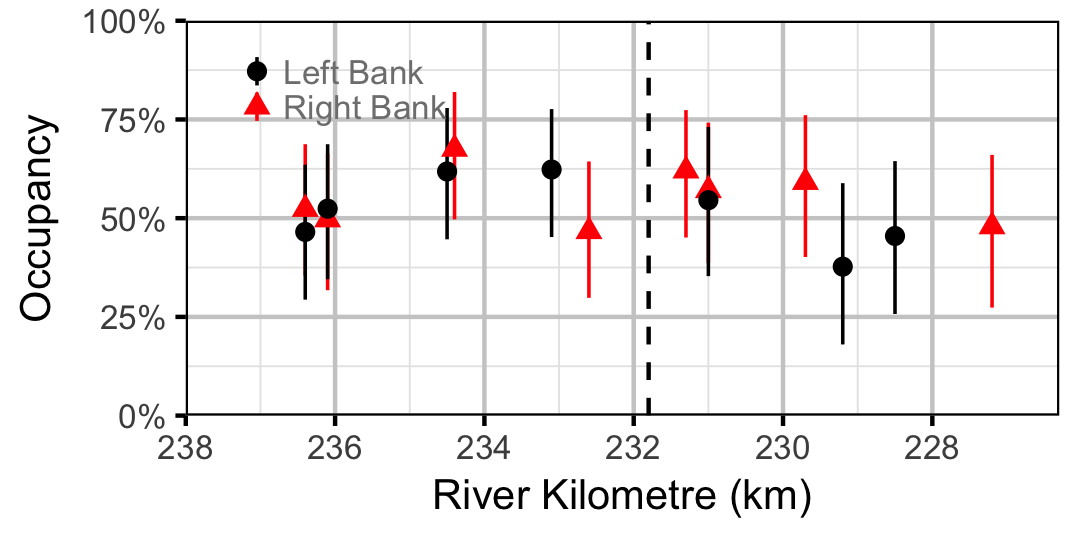
Northern Pikeminnow
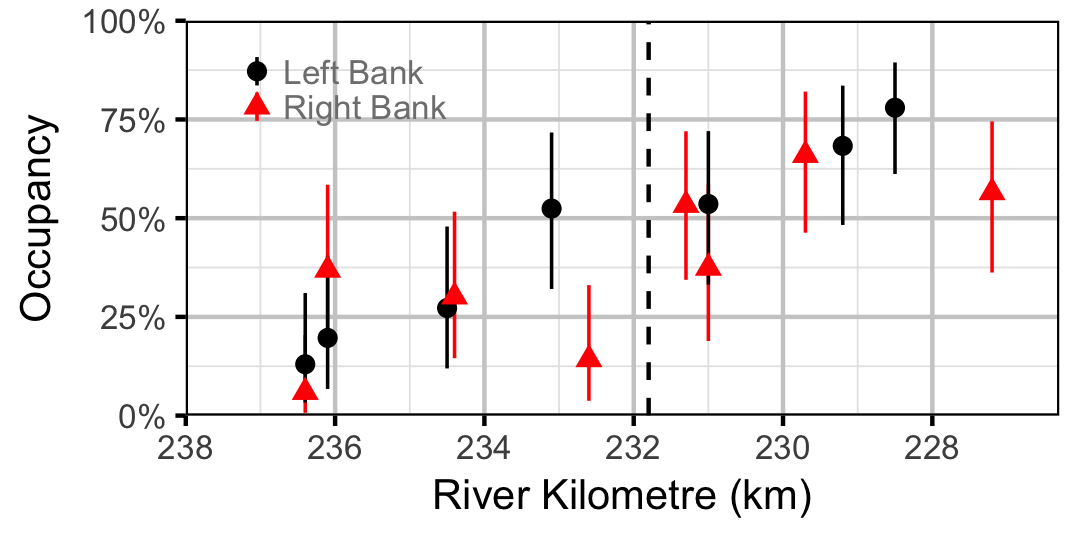
Redside Shiner
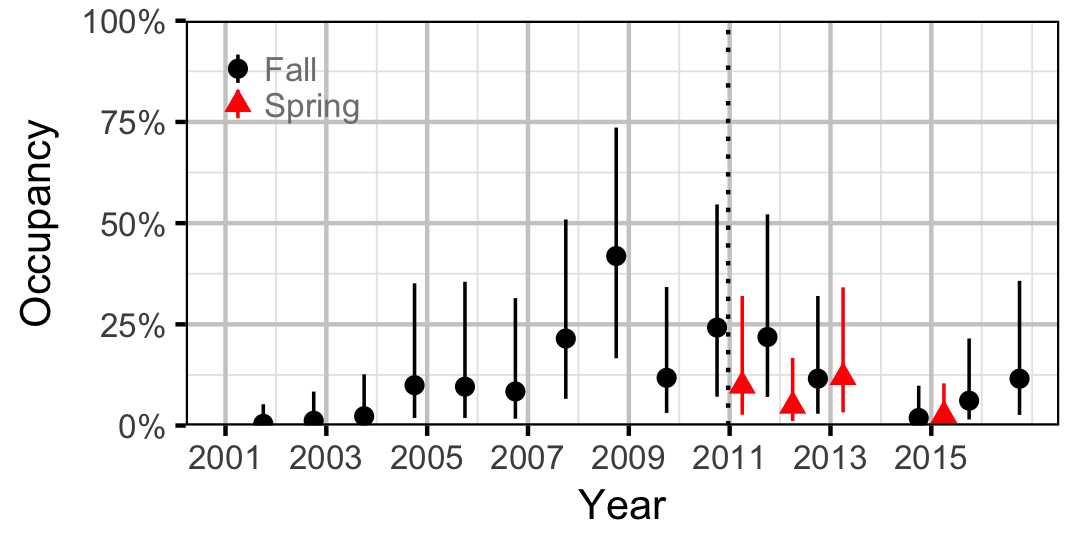
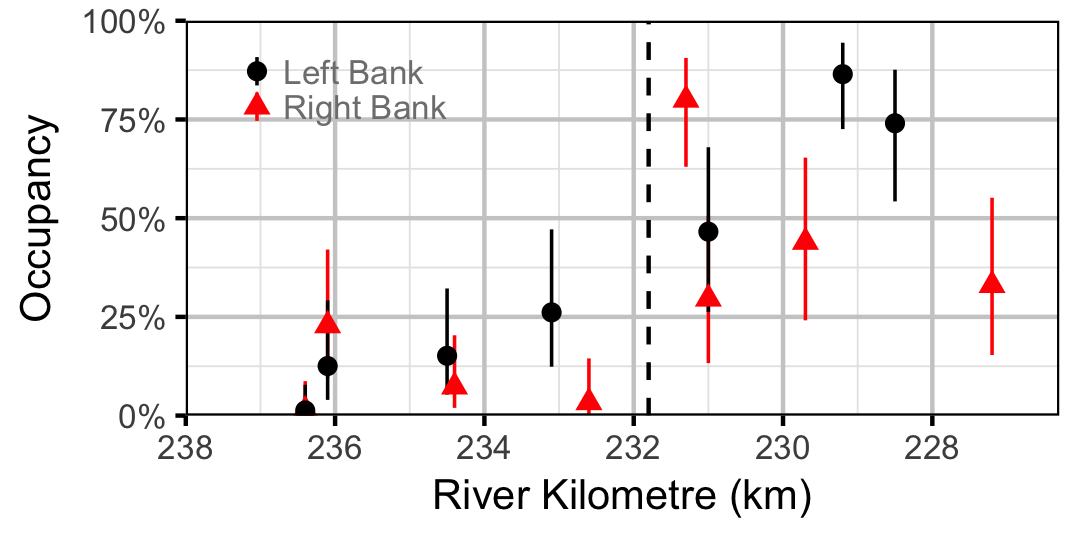
Sculpins
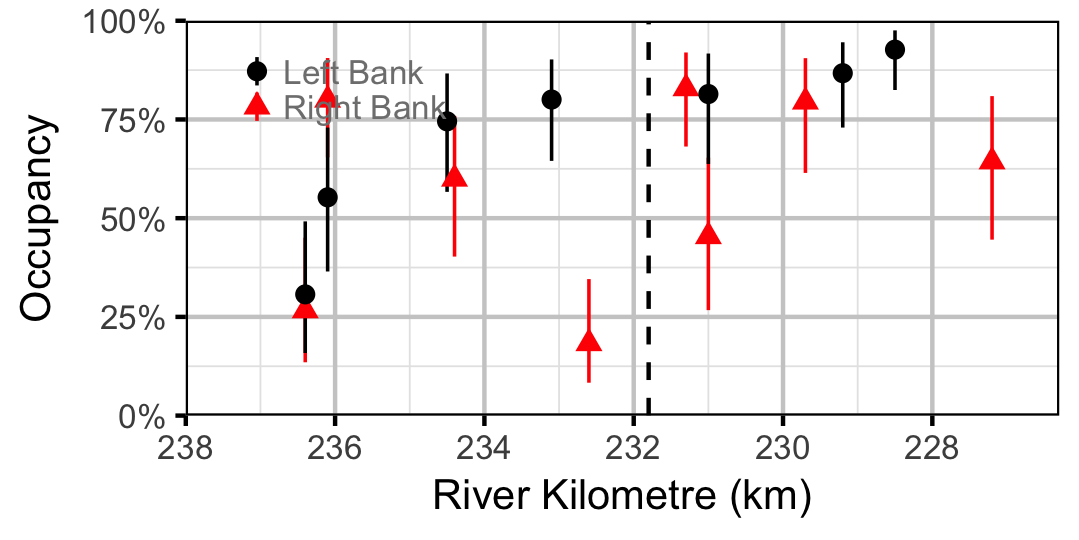
Species Richness
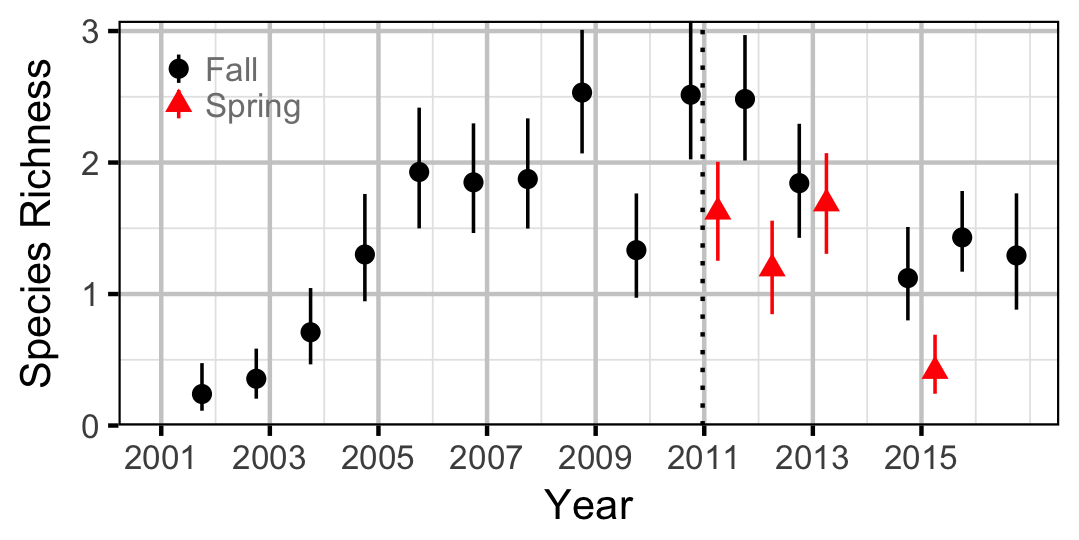
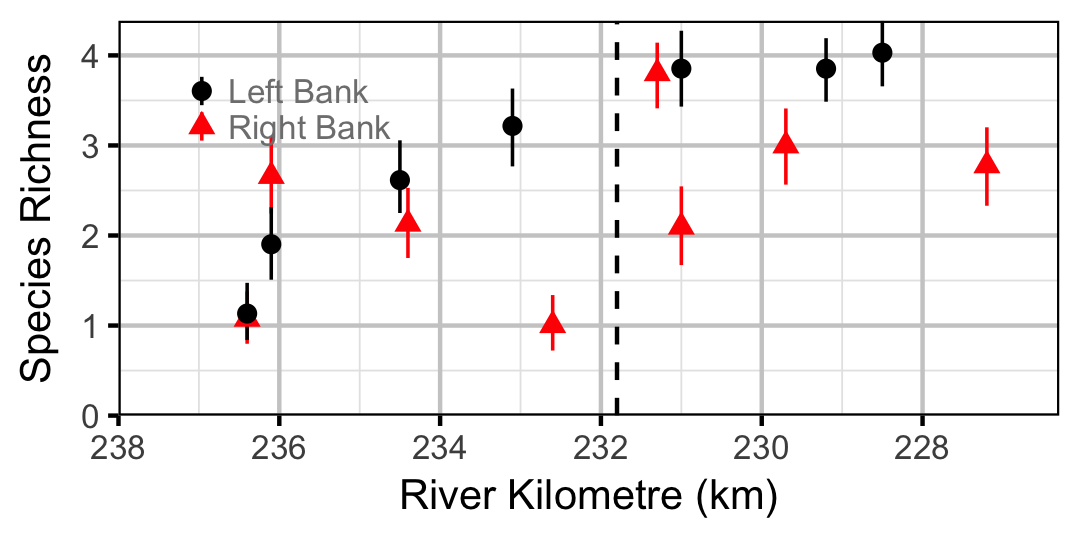
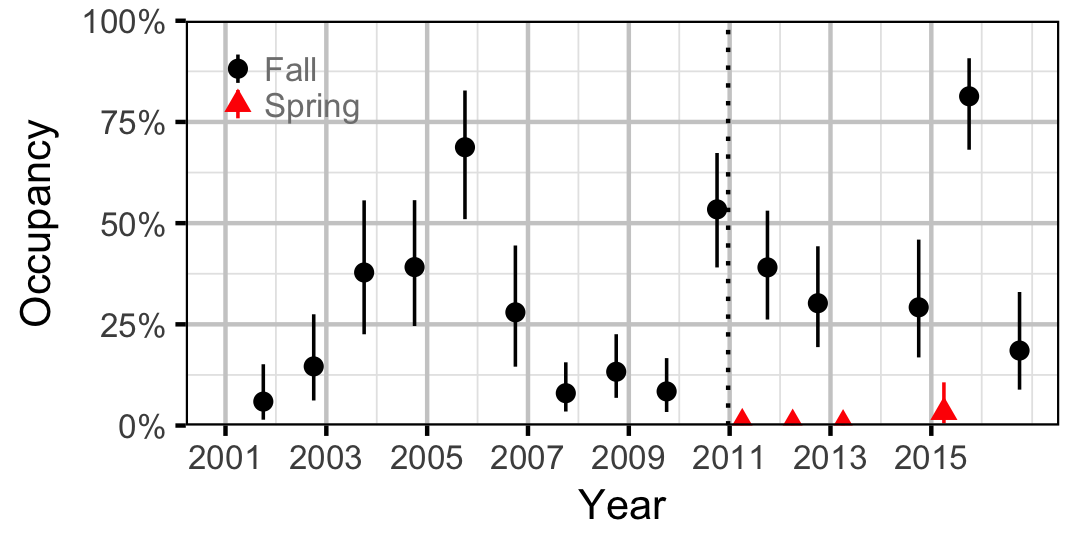
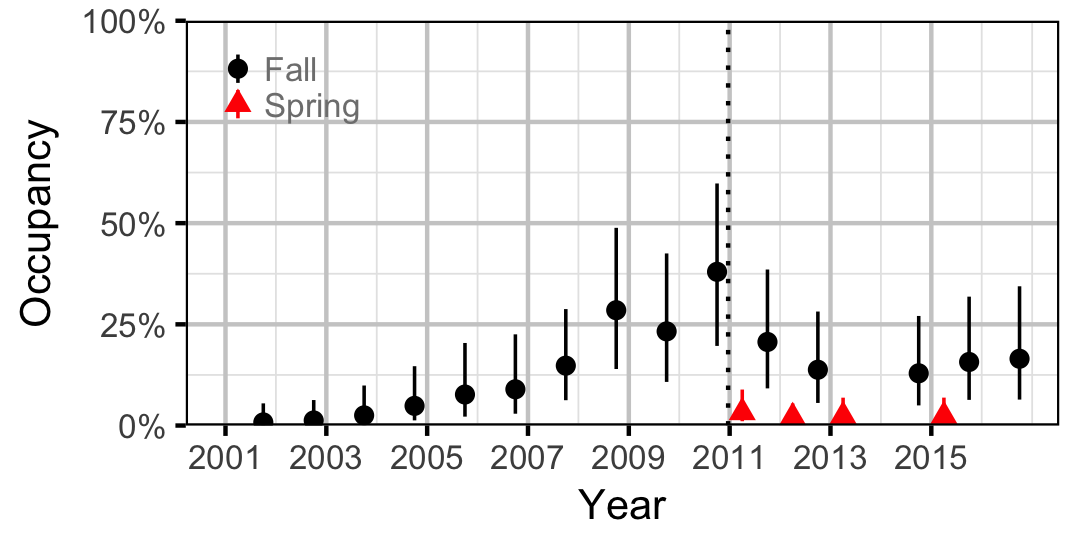
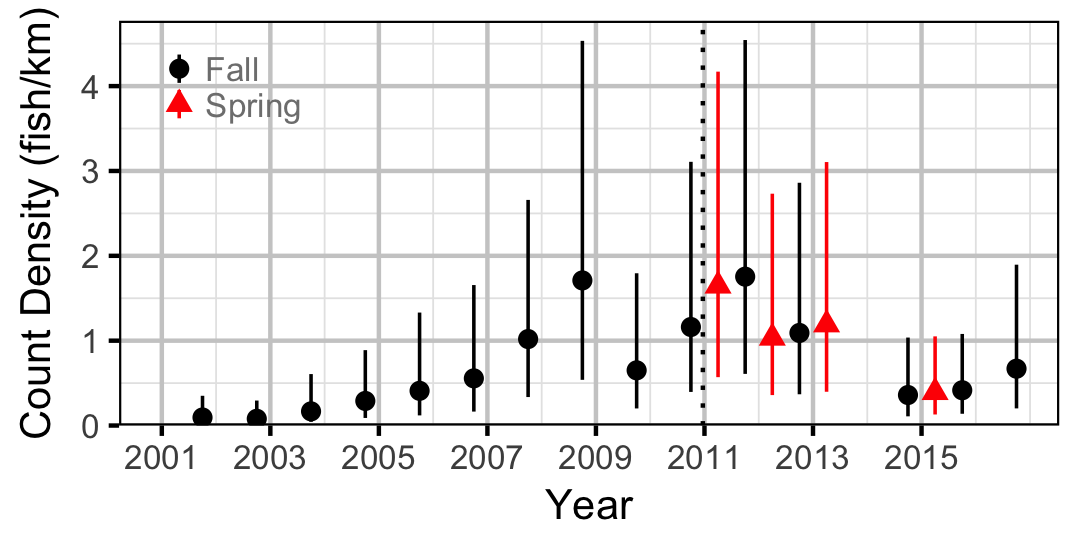
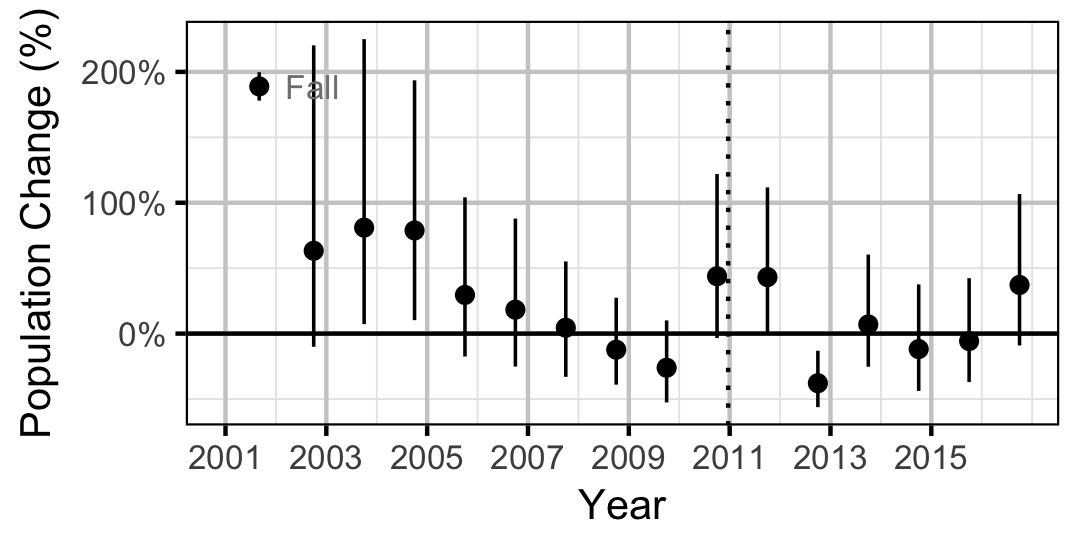
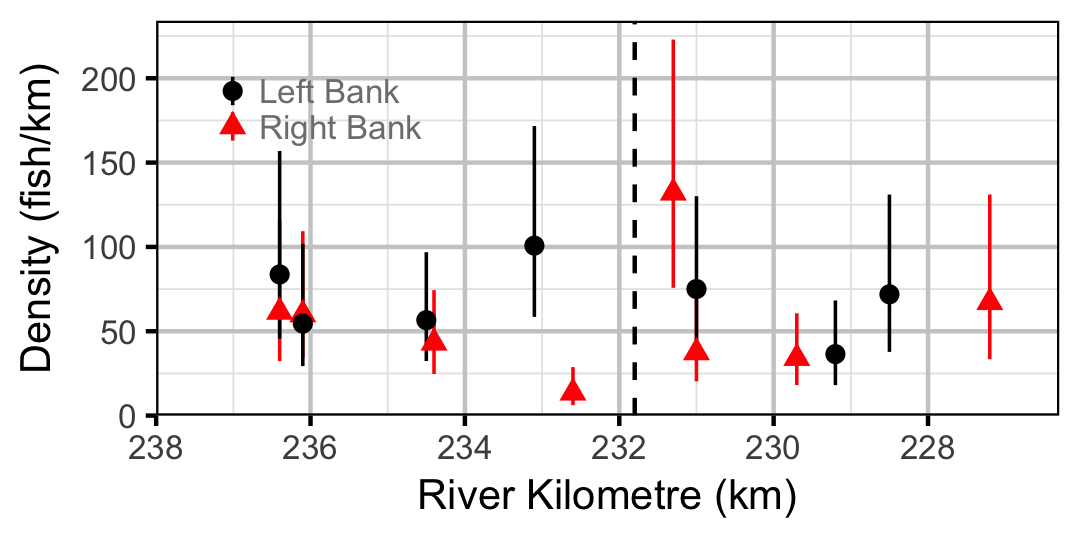
Count
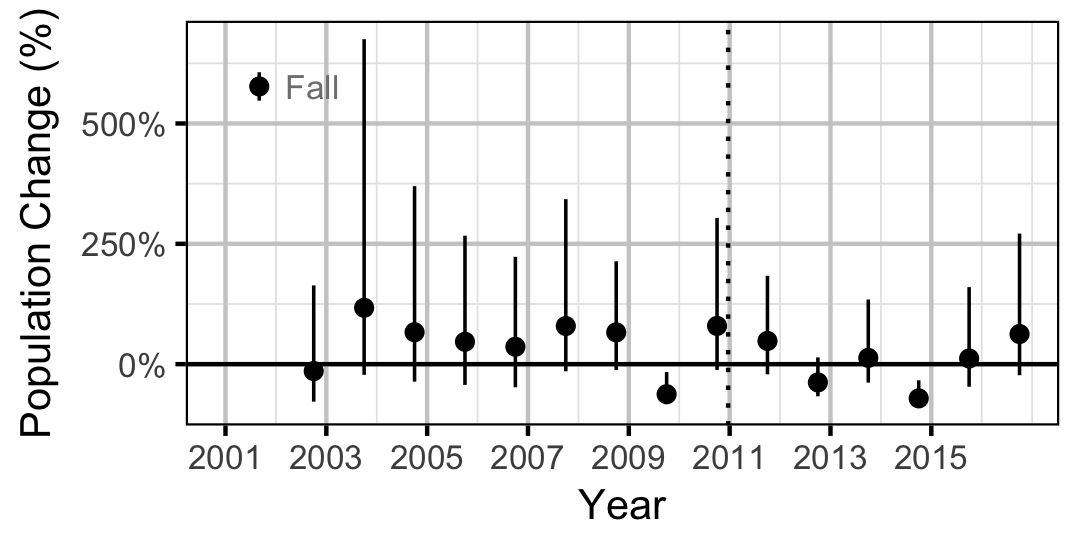
Rainbow Trout
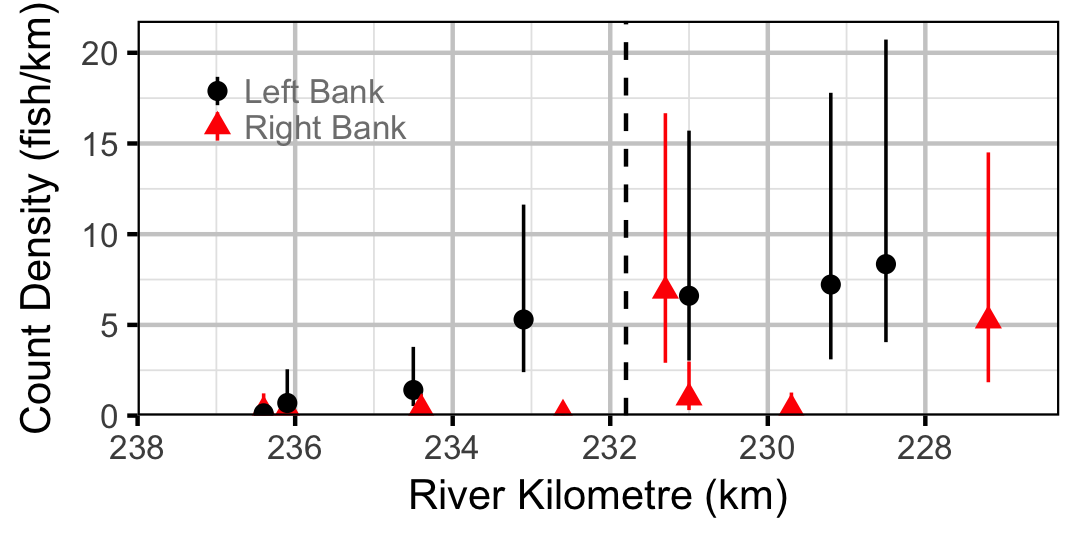
Burbot
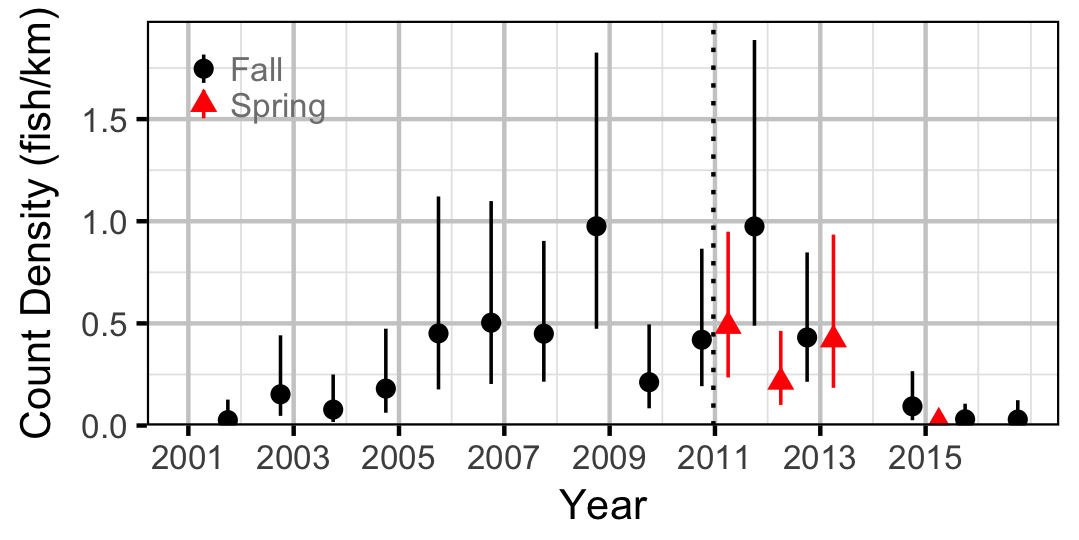
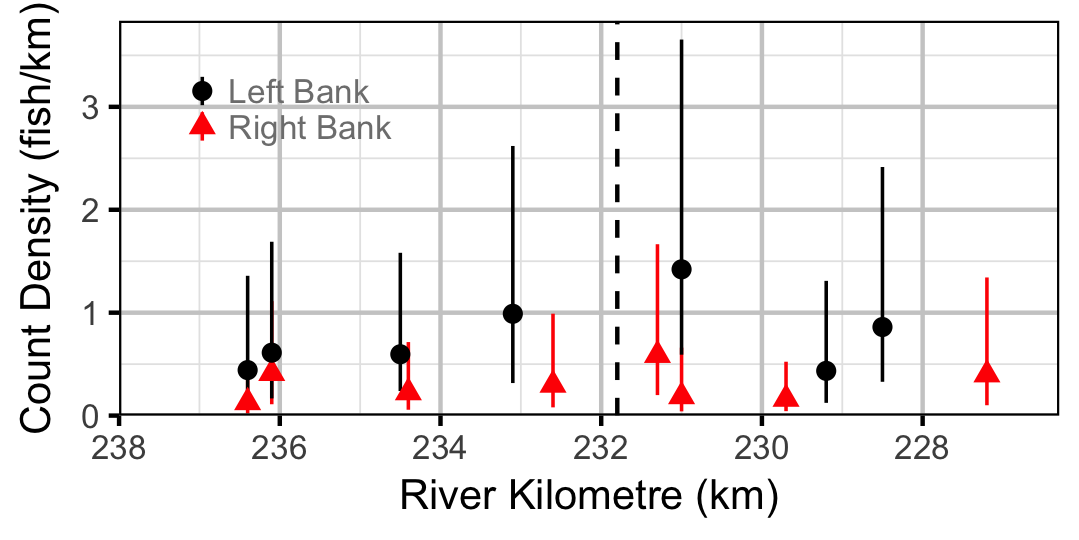
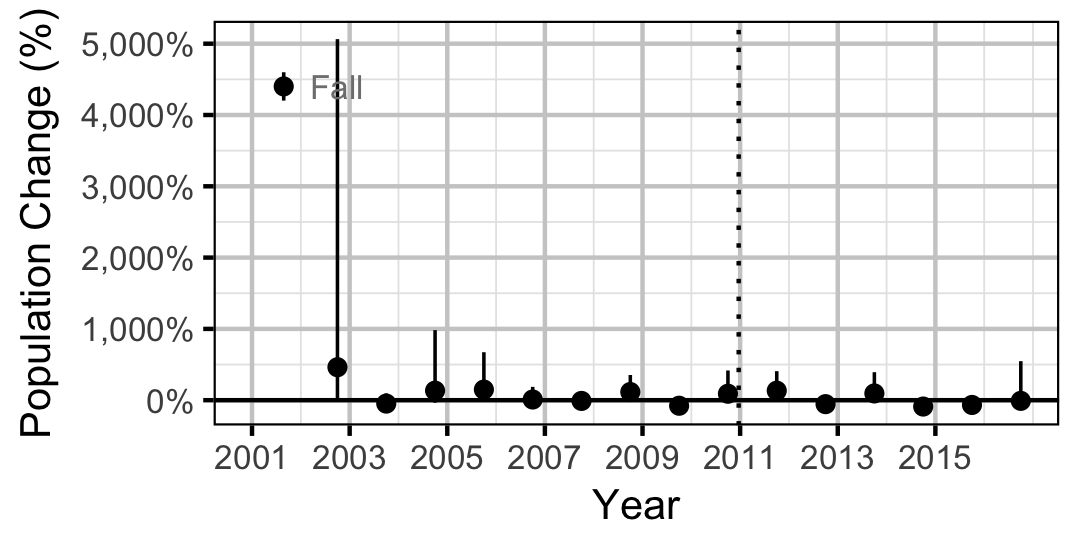
Northern Pikeminnow
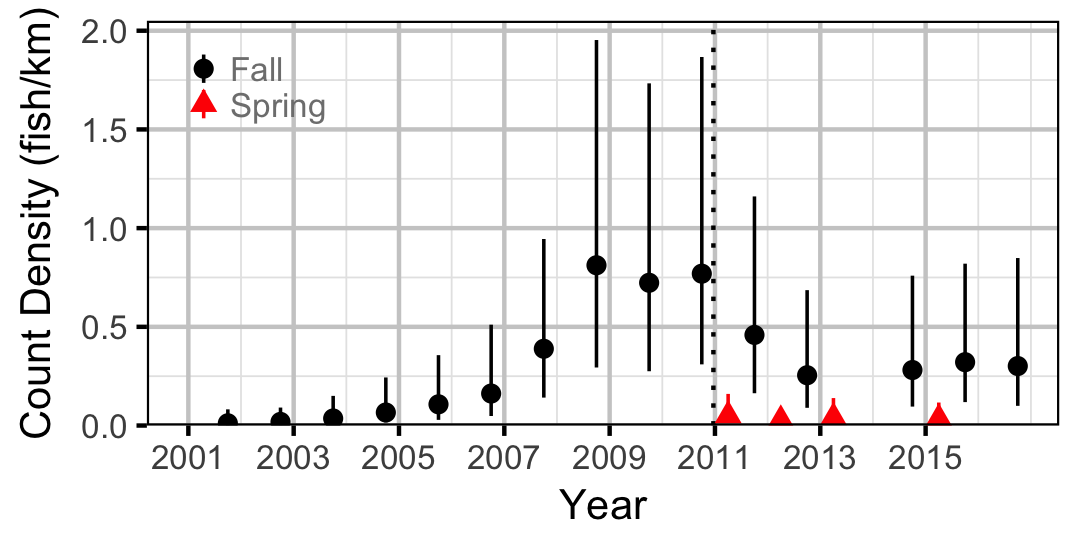
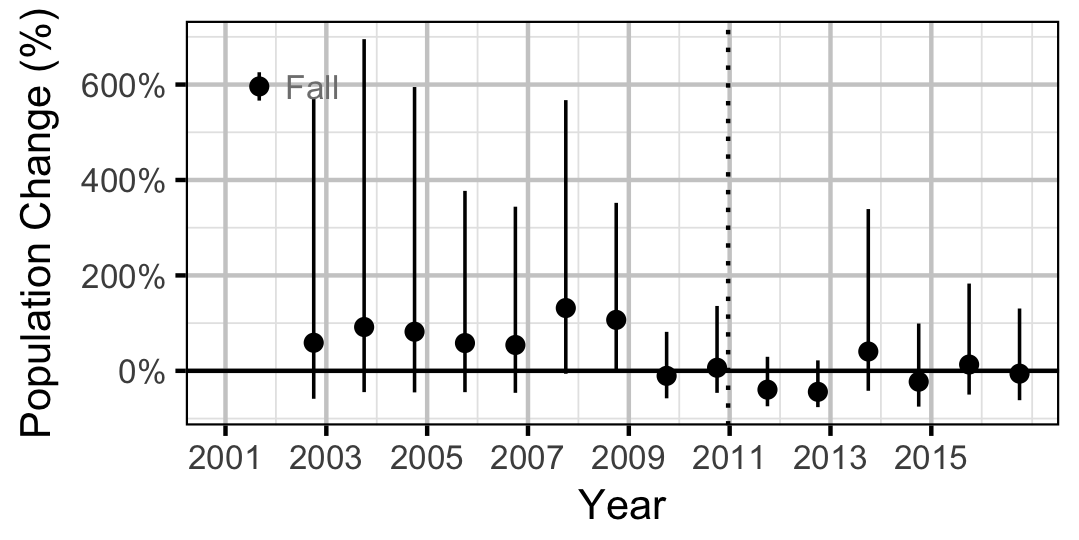
Suckers
Movement
Bull Trout
Mountain Whitefish
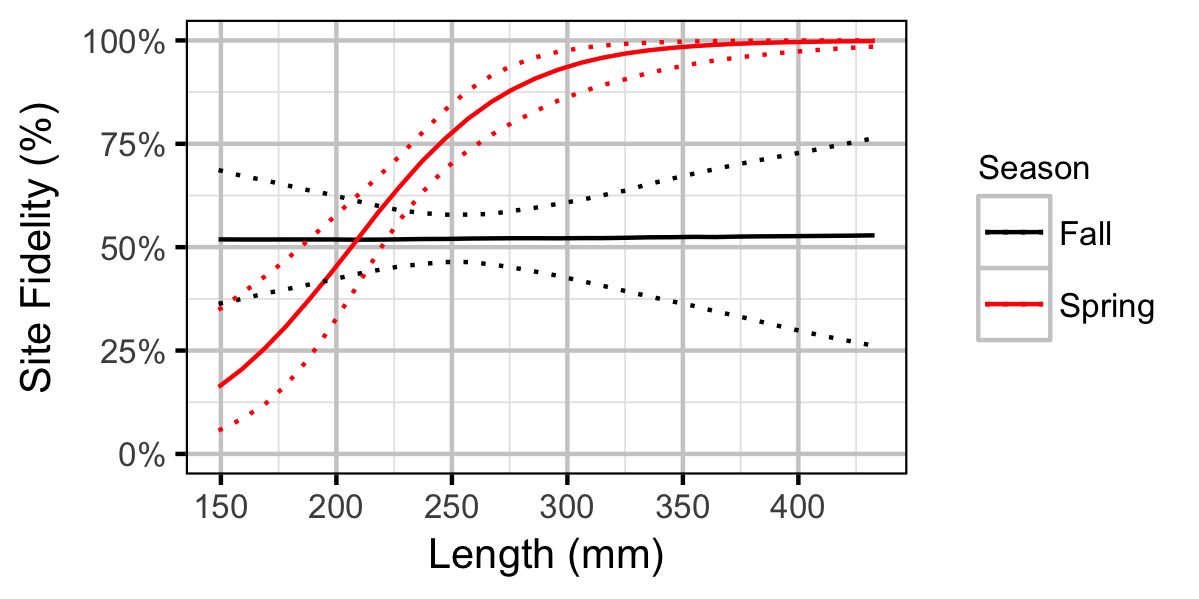
Rainbow Trout
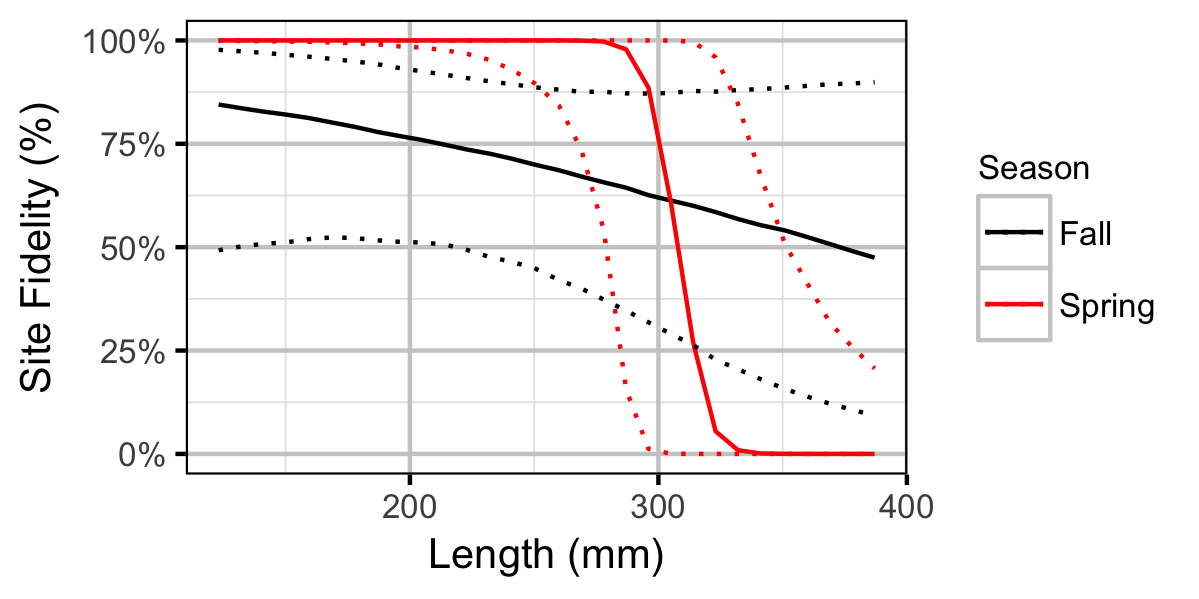
Largescale Sucker
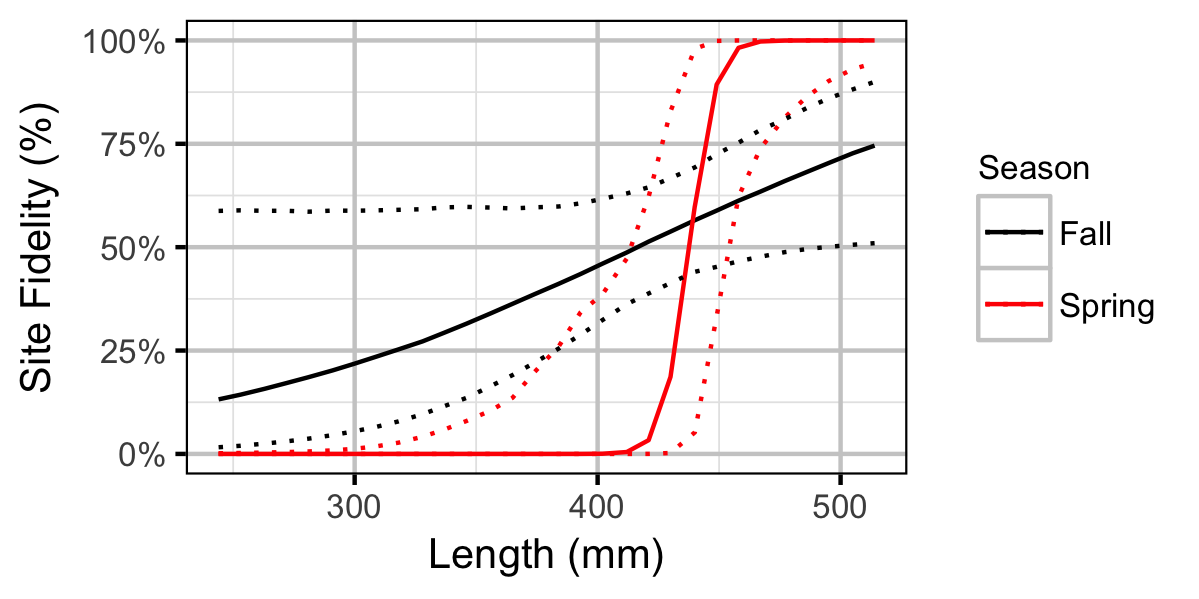
Observer Length Correction
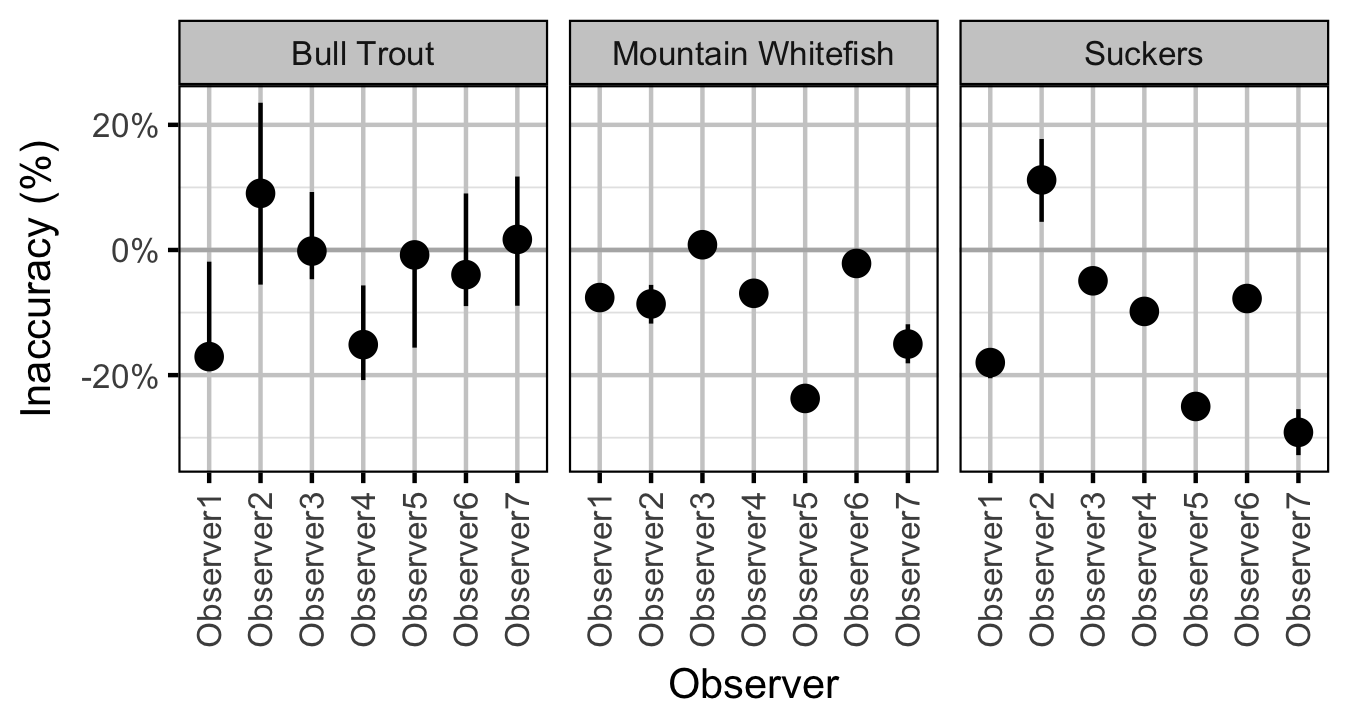
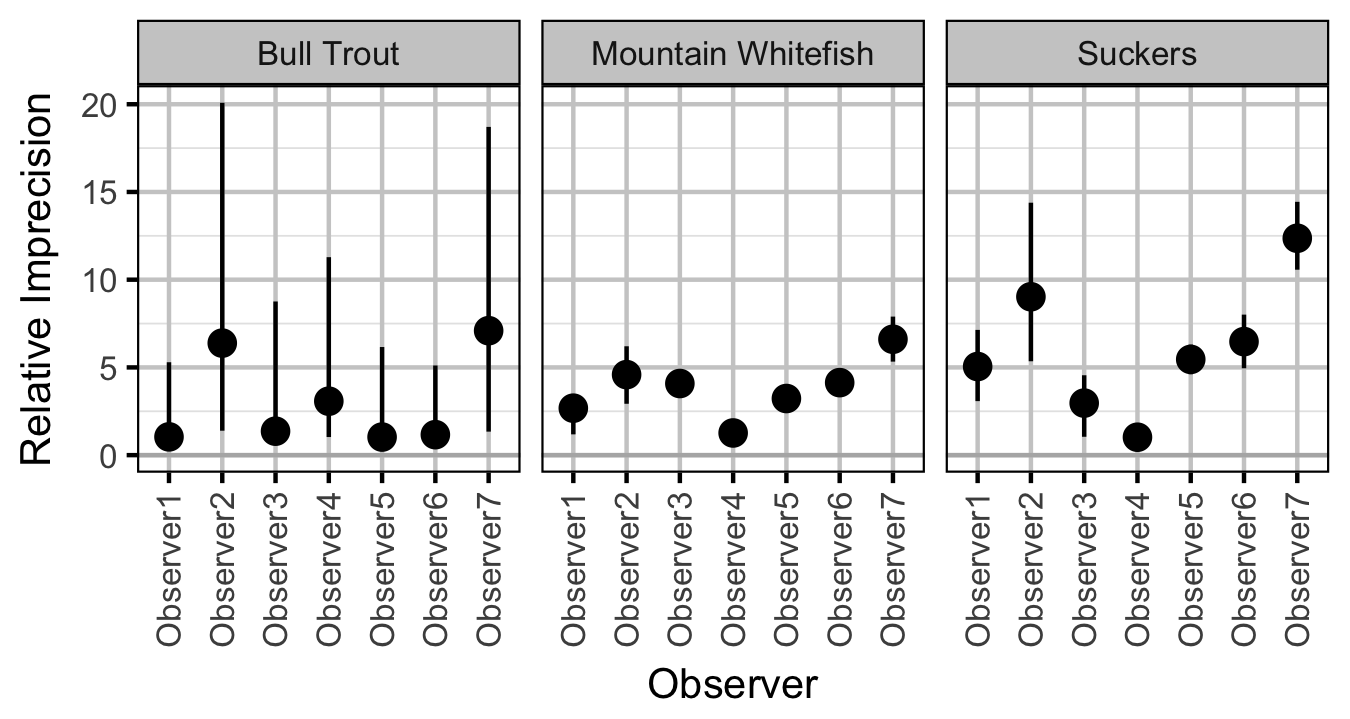
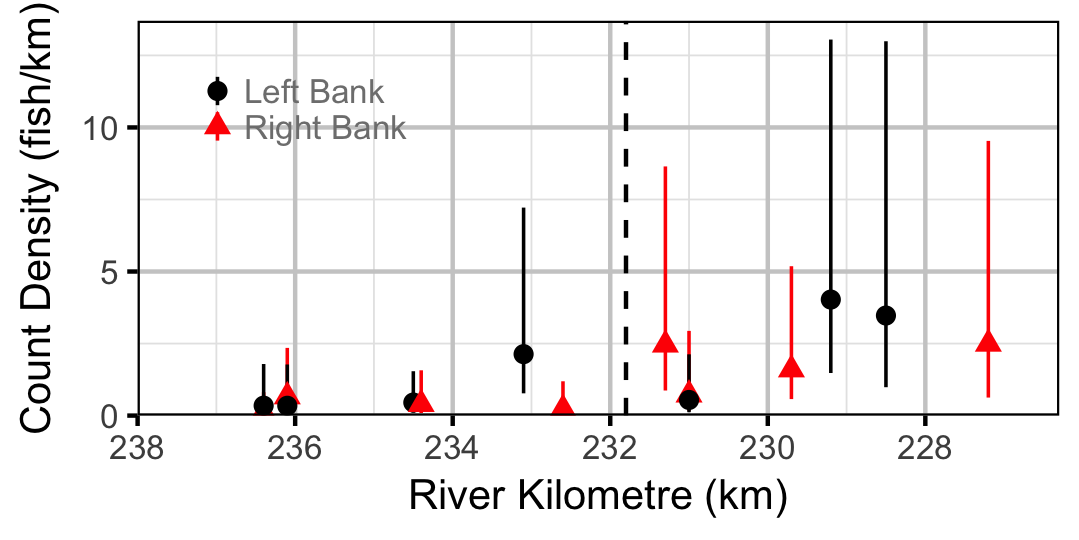
Abundance
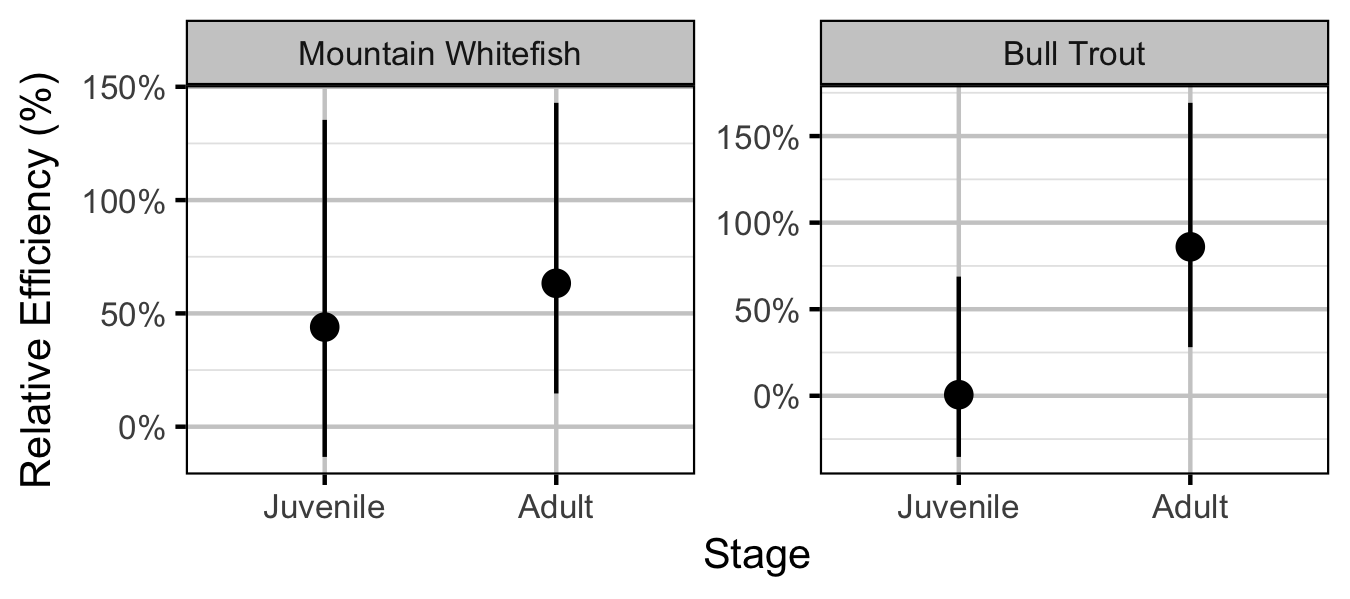
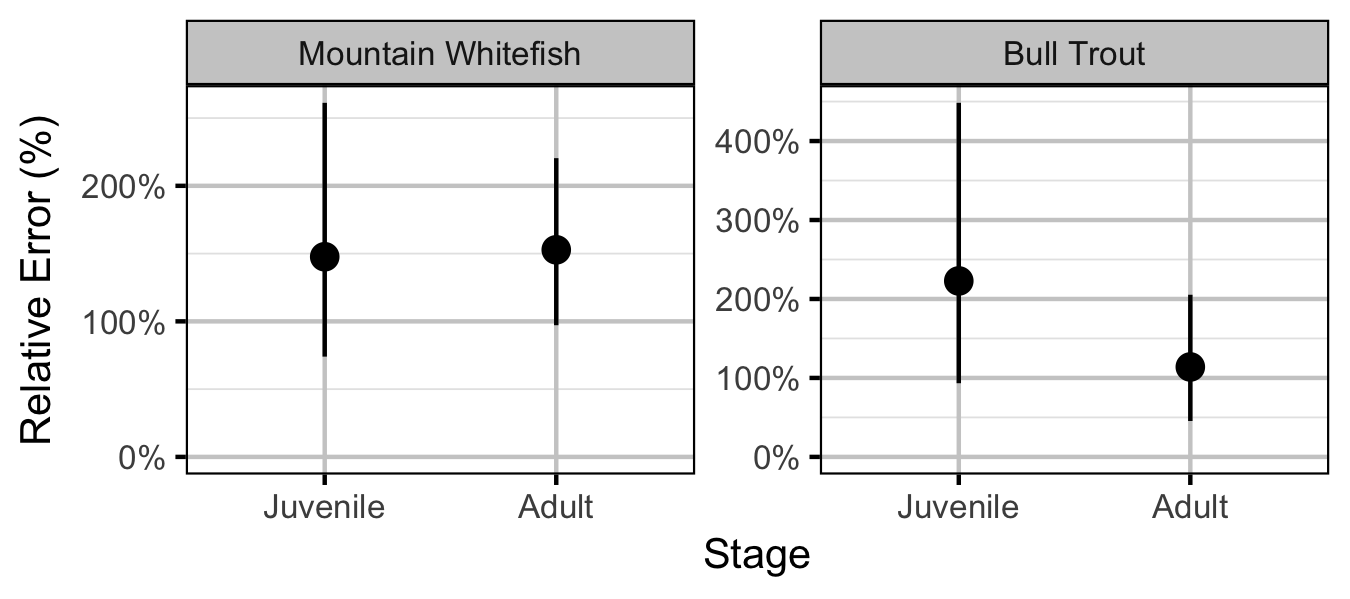
Bull Trout
Juvenile
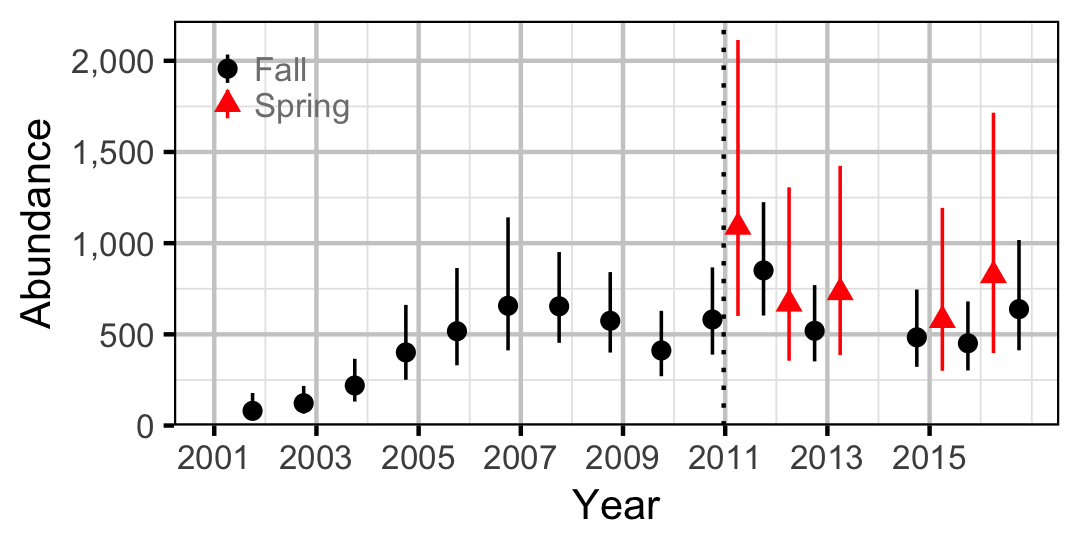
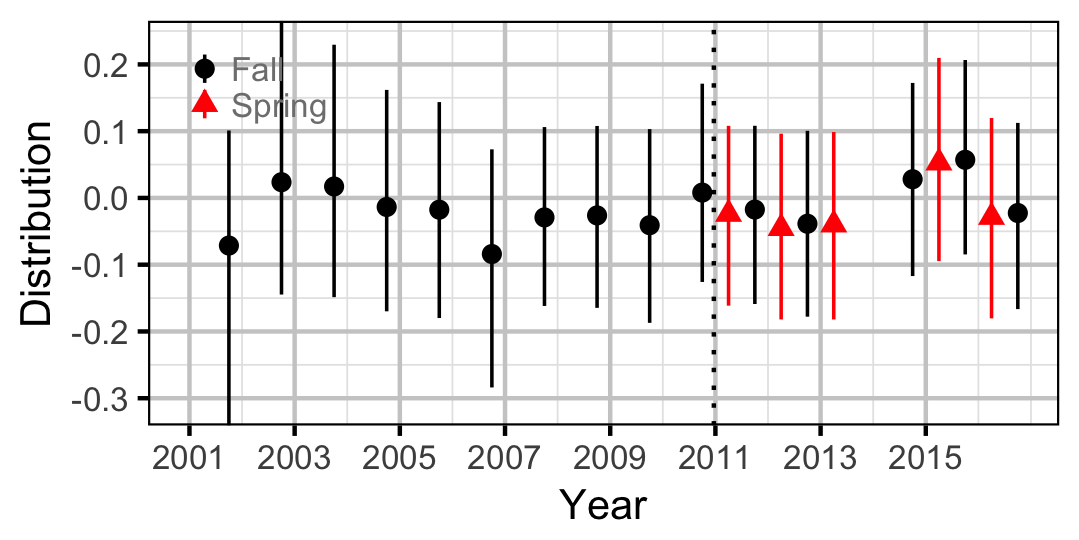
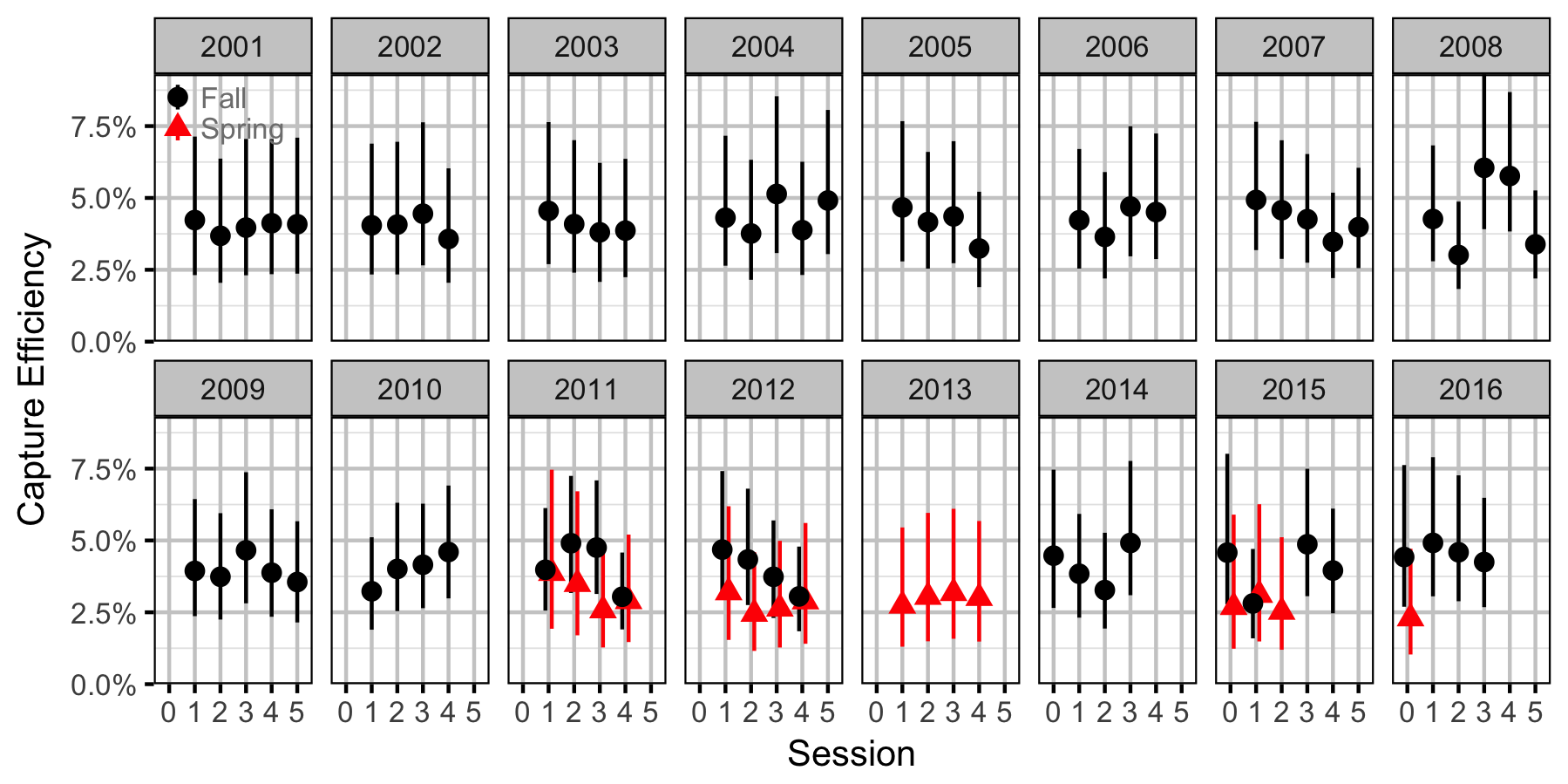
Adult
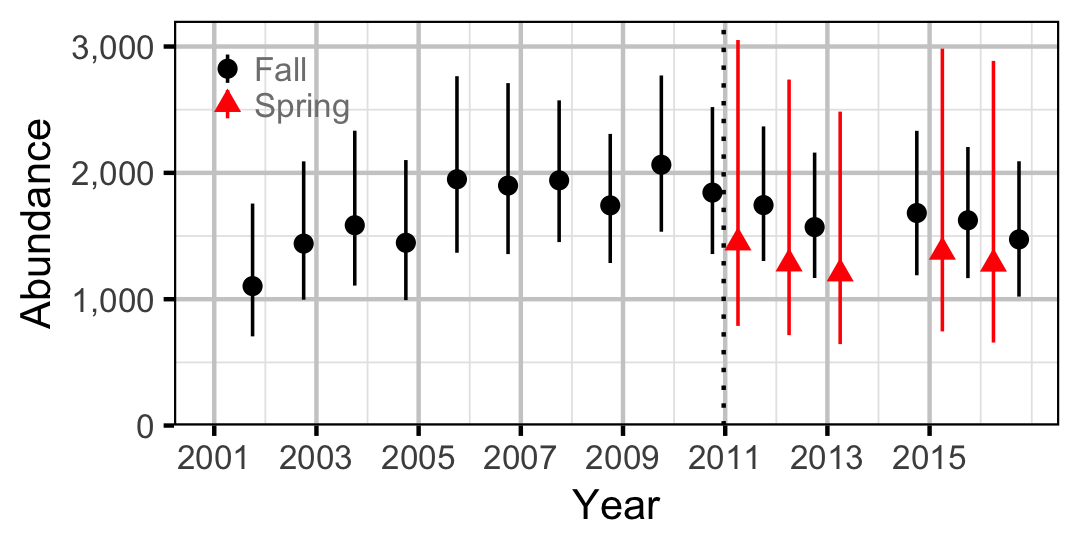
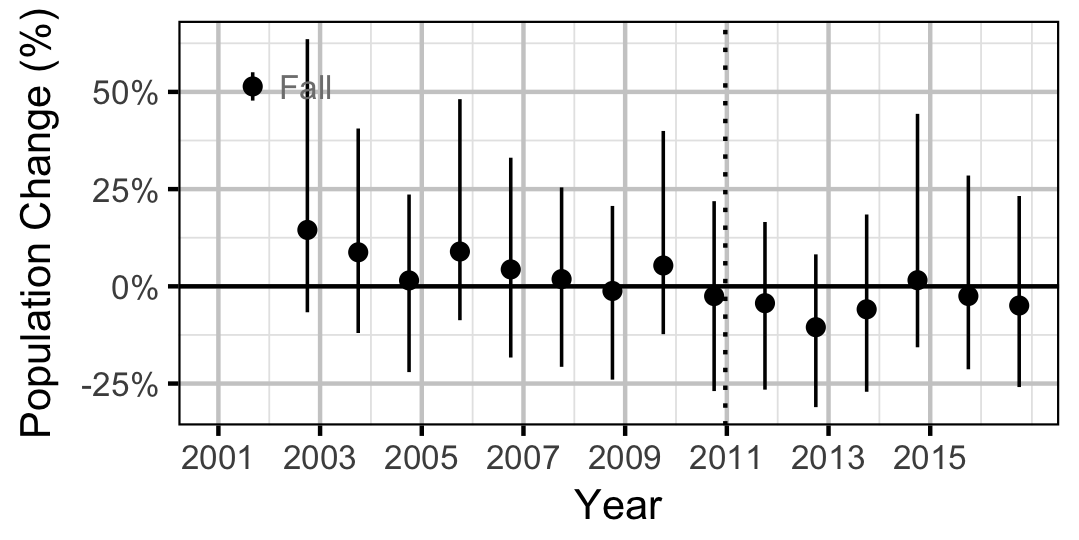
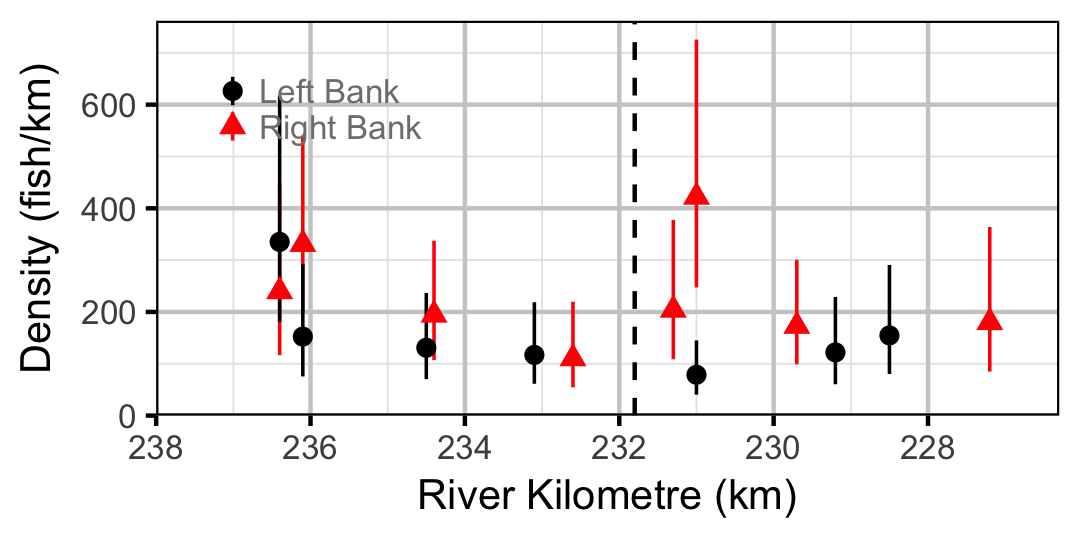
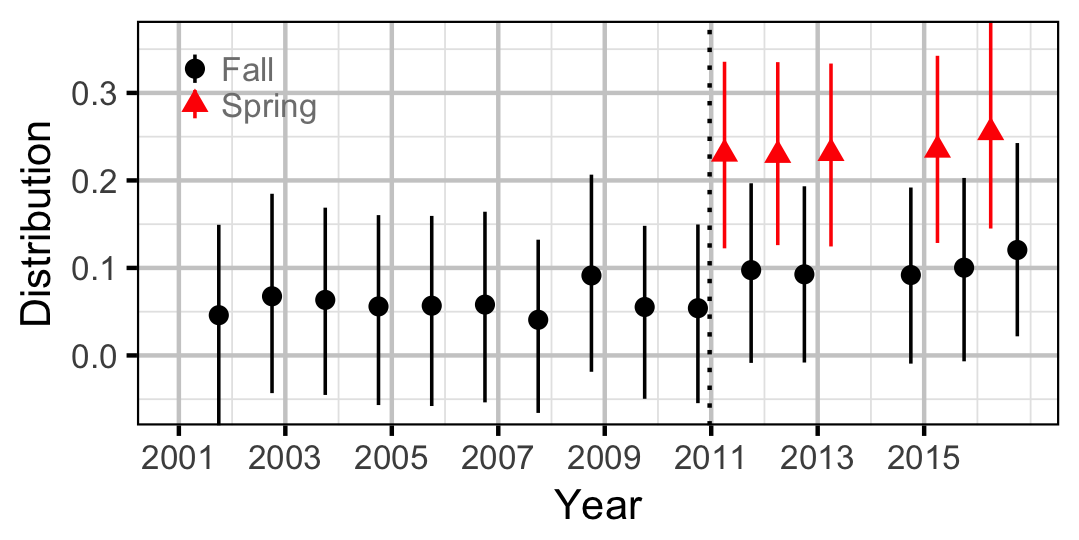
Mountain Whitefish
Juvenile
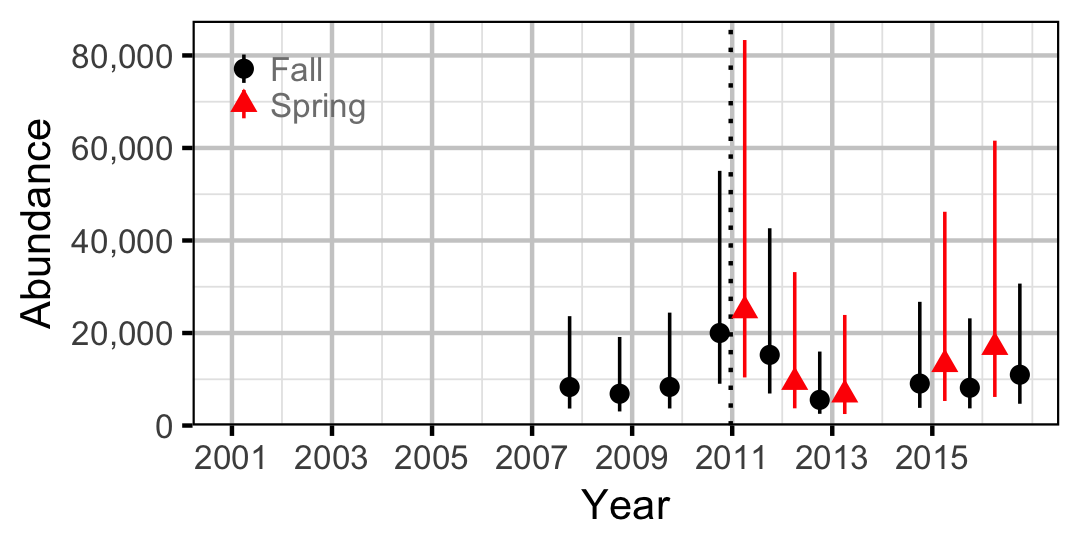
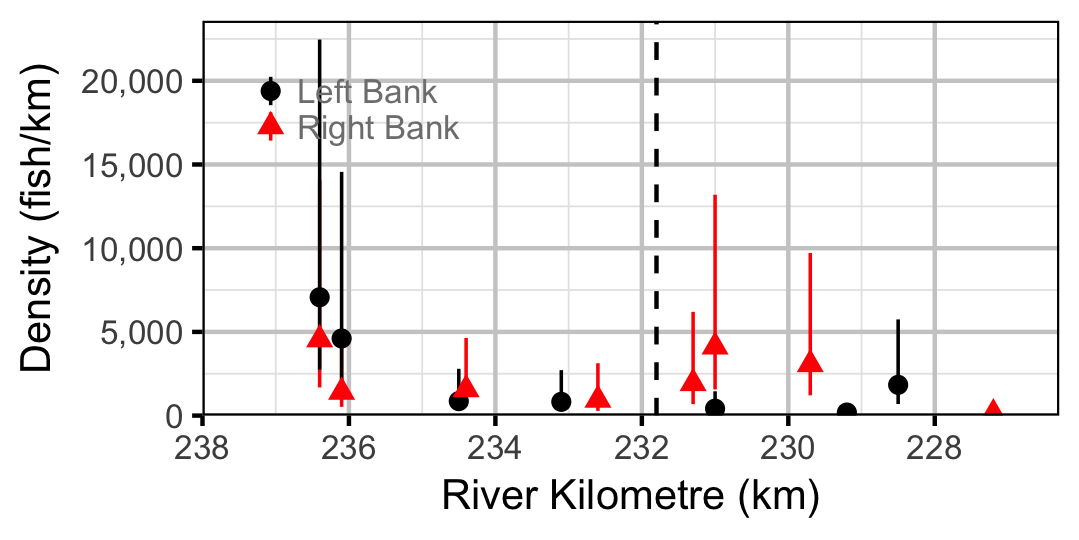
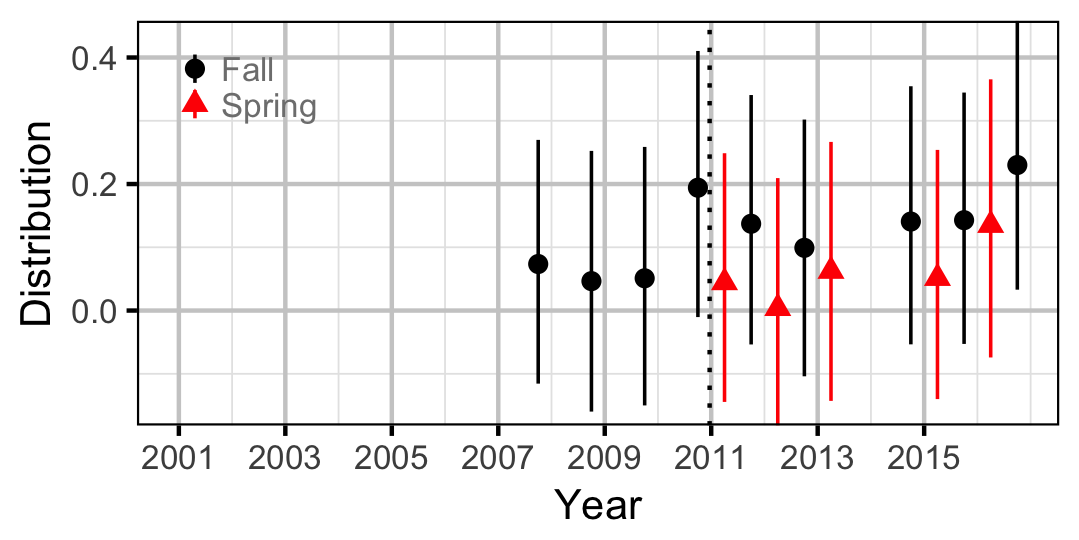
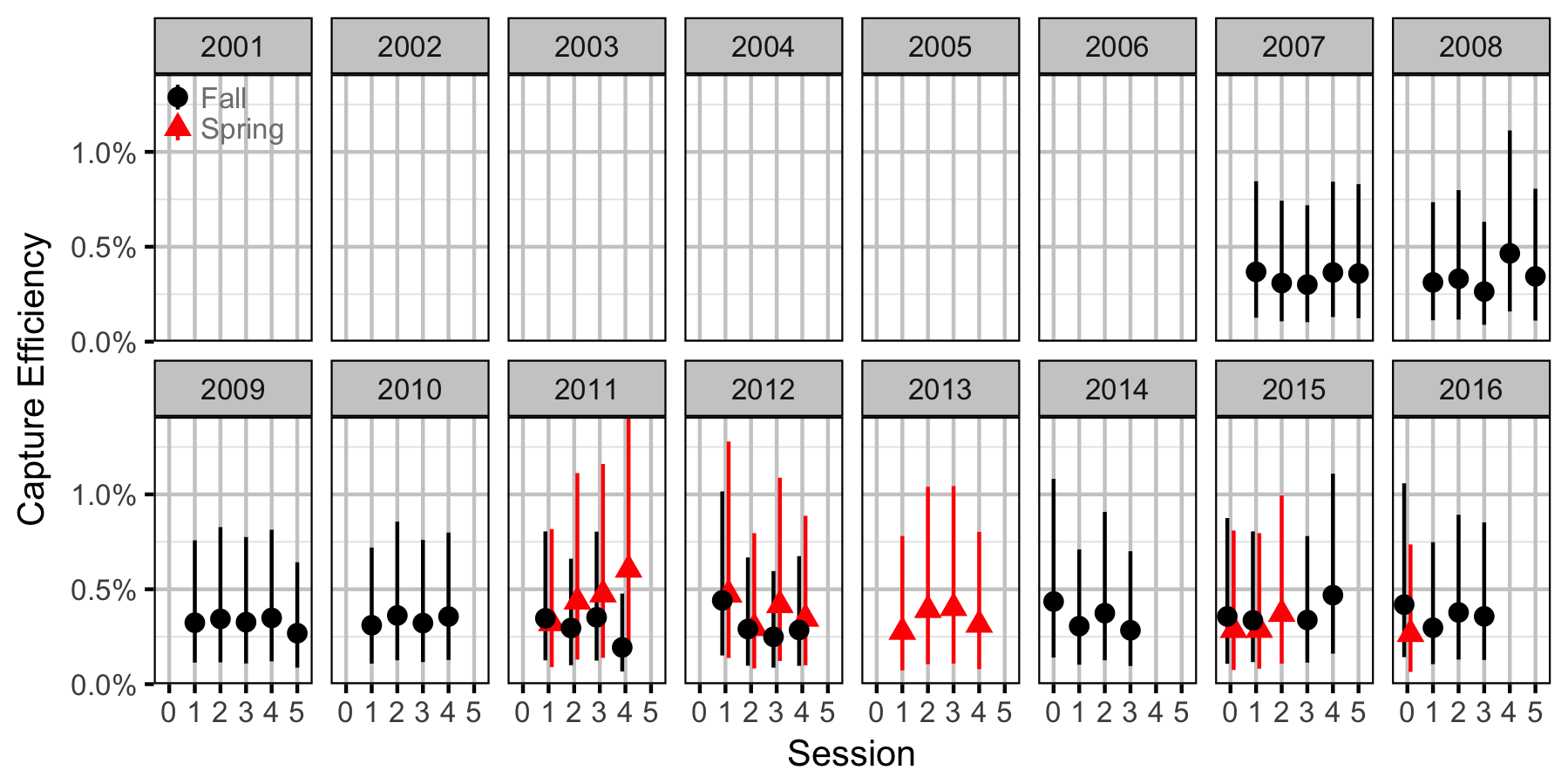
Adult
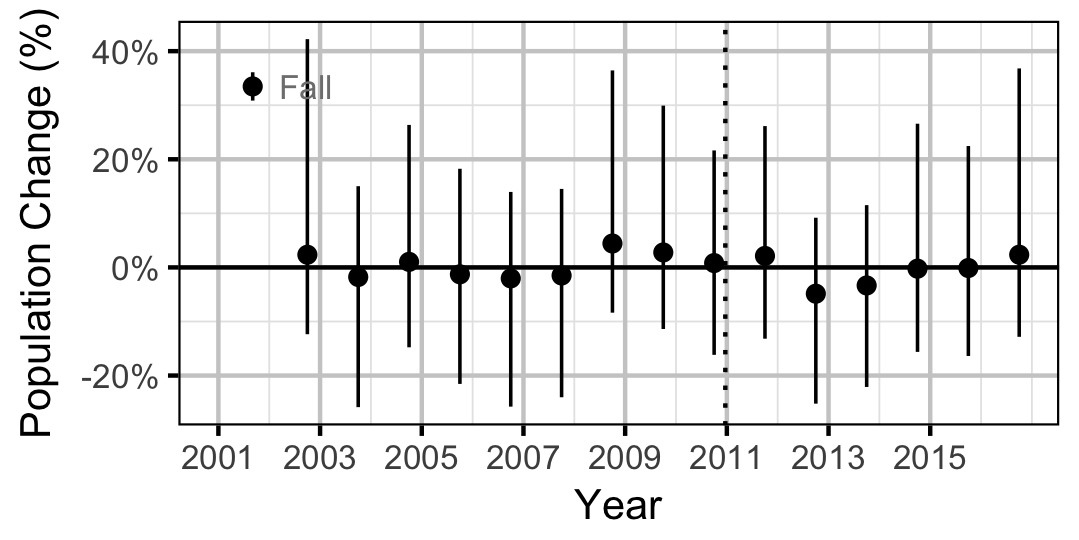
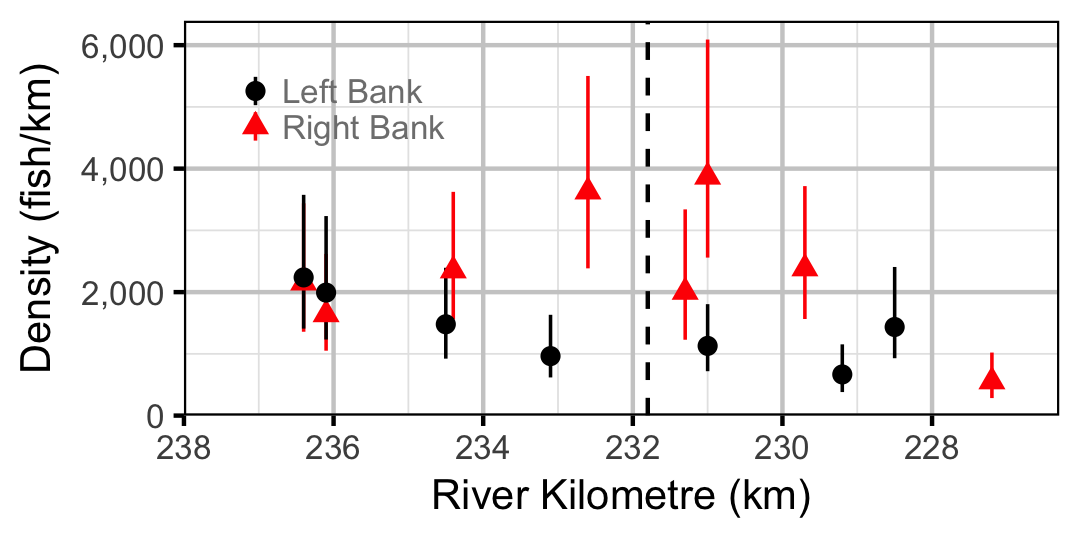
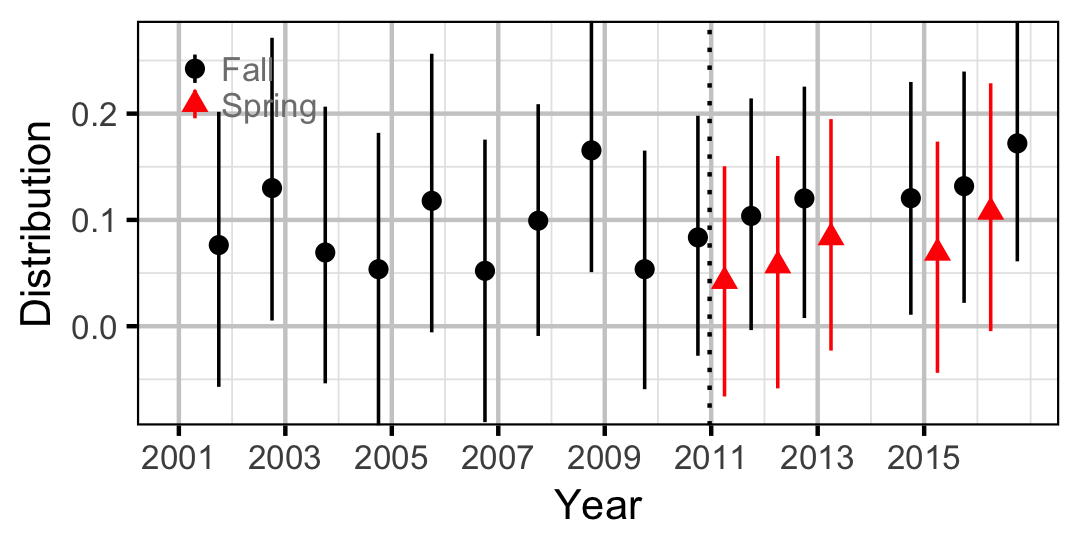
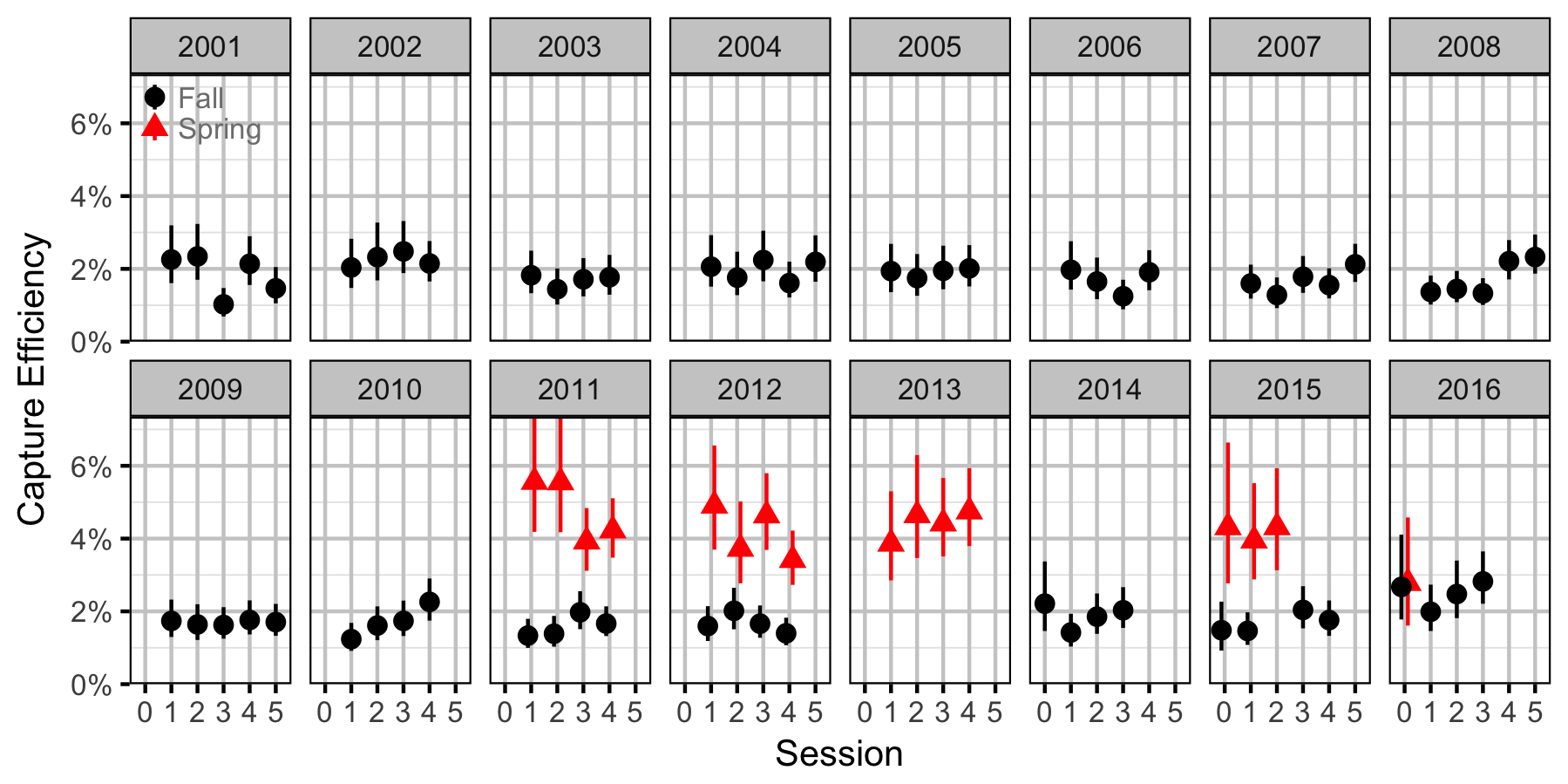
Rainbow Trout
Adult
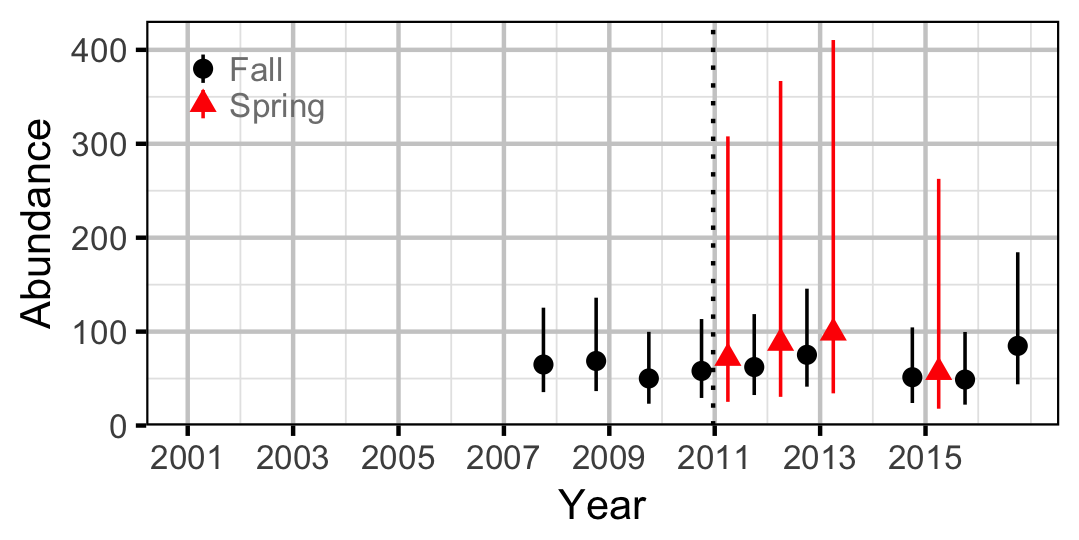
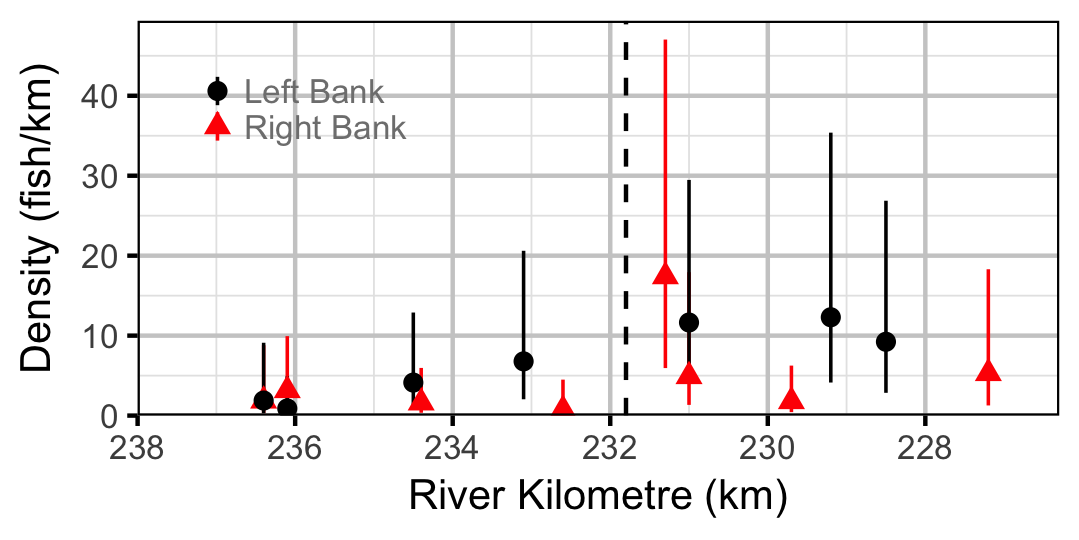
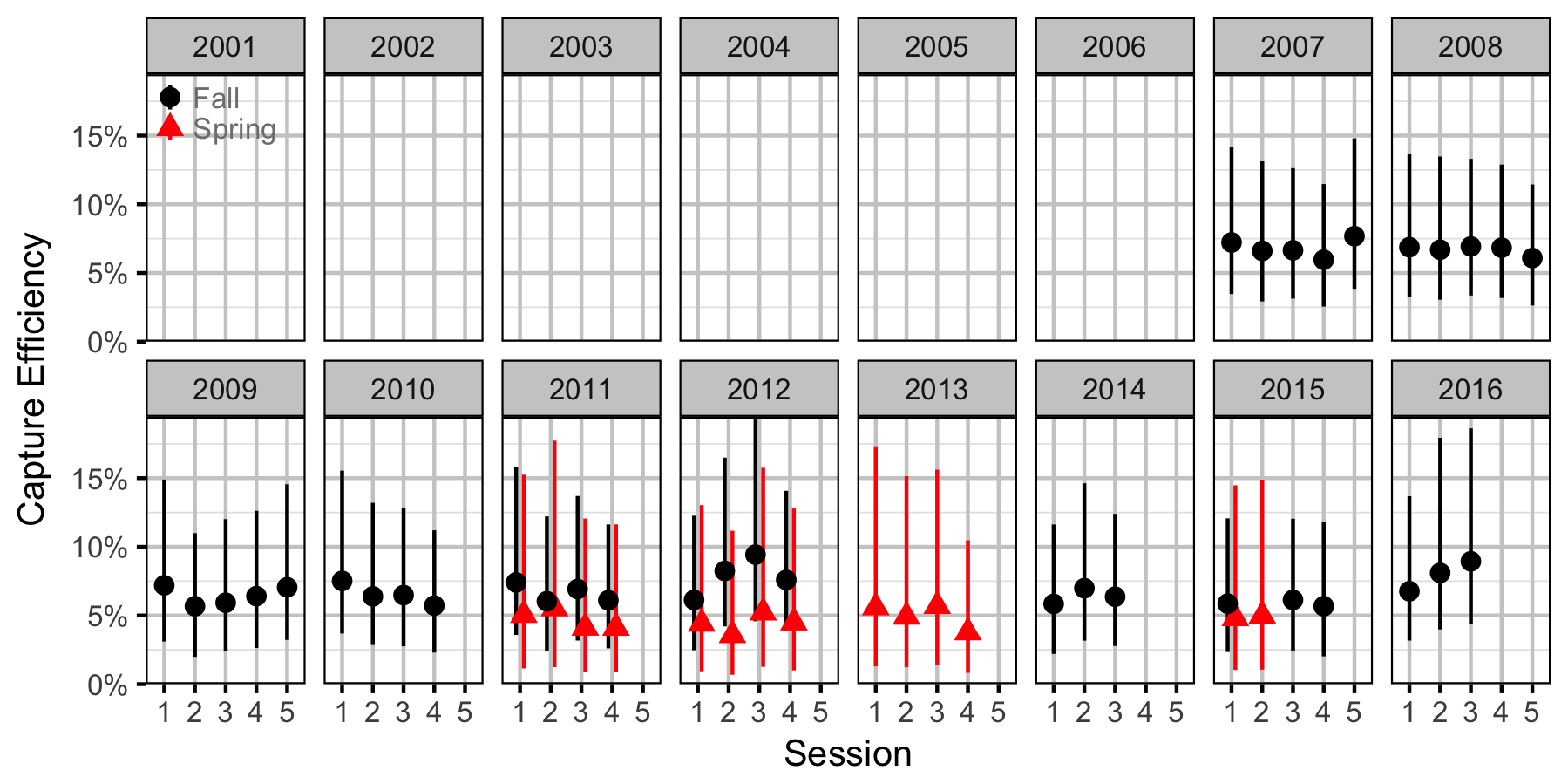
Largescale Sucker
Adult
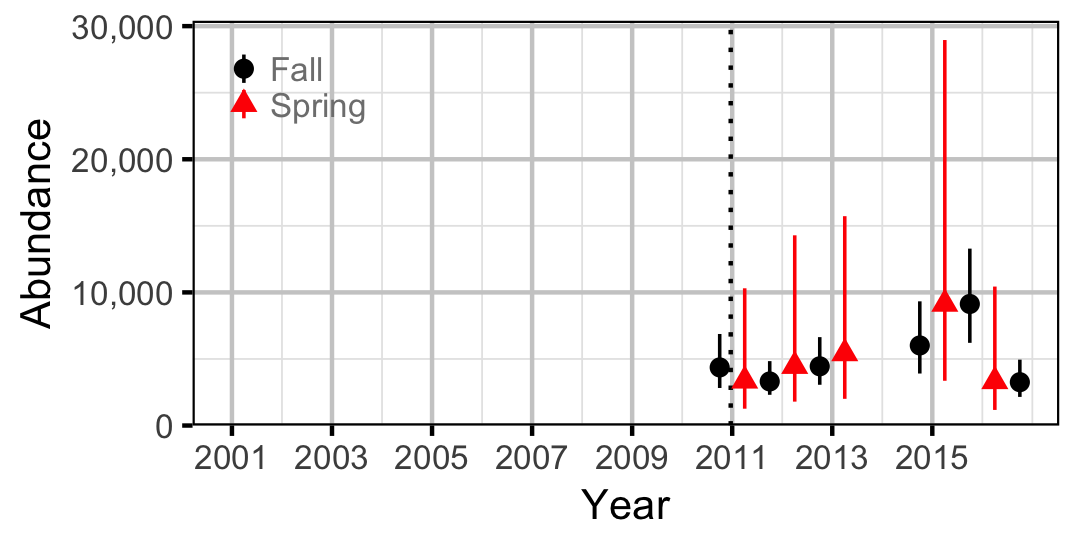
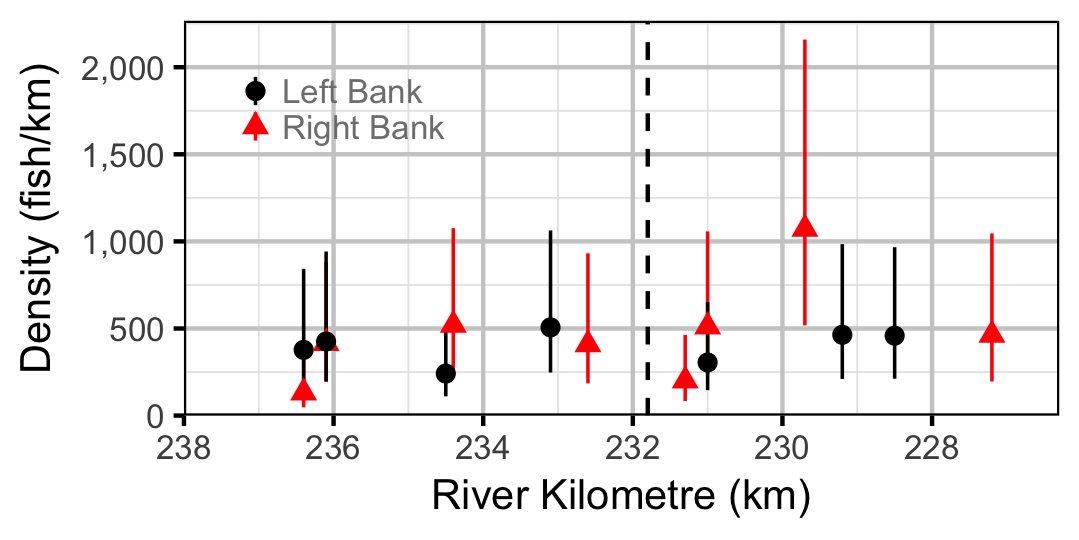
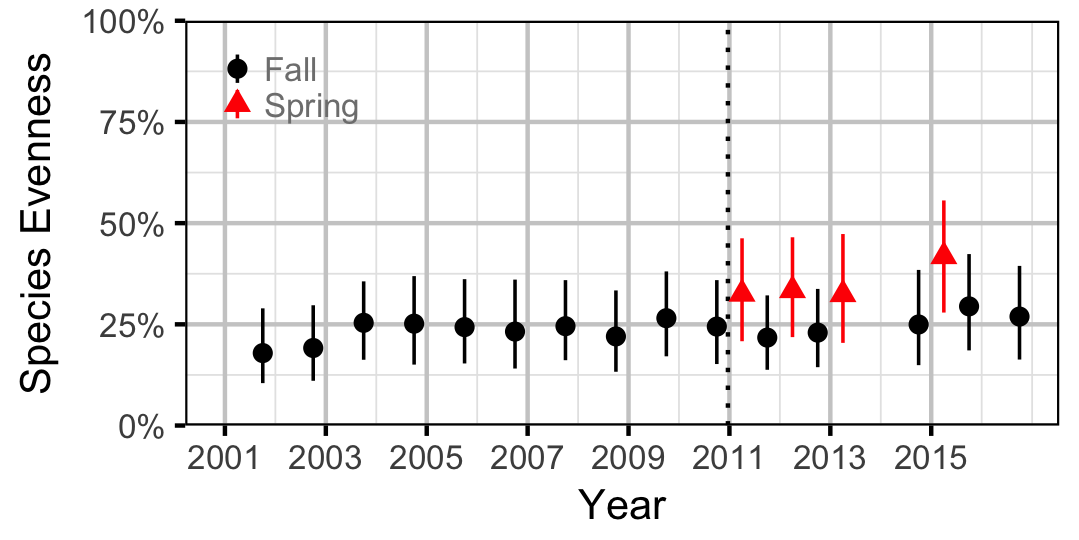
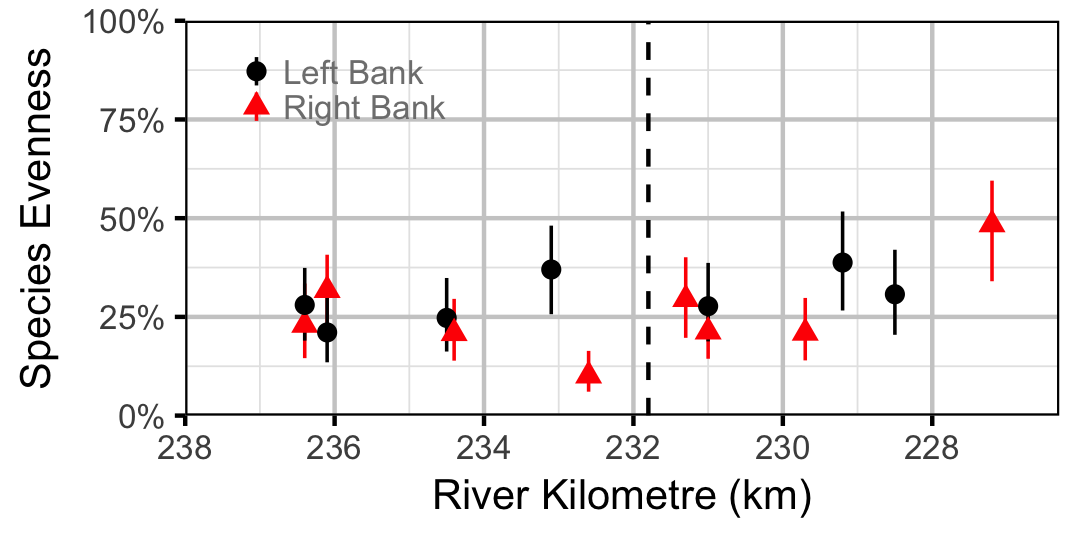
Species Diversity (Evenness)
Significance
Table 69. The significance levels for the management hypotheses tested in the analyses where Condition1 is the effect of the regime change on weight for big and small fish and Condition2 is the effect of the regime change on big relative to small fish. The Direction column indicates whether significant changes were positive or negative.
| Test | Species | Stage | Significance | Direction |
|---|---|---|---|---|
| Abundance | Mountain Whitefish | Adult | 0.7370 | |
| Abundance | Mountain Whitefish | Juvenile | 0.5500 | |
| Abundance | Bull Trout | Adult | 0.2730 | |
| Abundance | Bull Trout | Juvenile | 0.1640 | |
| Condition1 | Mountain Whitefish | 0.0050 | - | |
| Condition1 | Rainbow Trout | 0.5840 | ||
| Condition1 | Bull Trout | 0.0005 | - | |
| Condition2 | Mountain Whitefish | 0.3110 | ||
| Condition2 | Rainbow Trout | 0.5300 | ||
| Condition2 | Bull Trout | 0.3690 | ||
| Count | Rainbow Trout | 0.2060 | ||
| Count | Sucker | 0.7600 | ||
| Count | Burbot | 0.1530 | ||
| Count | Northern Pikeminnow | 0.2260 | ||
| Distribution | Mountain Whitefish | Adult | 0.2620 | |
| Distribution | Mountain Whitefish | Juvenile | 0.3820 | |
| Distribution | Bull Trout | Adult | 0.2390 | |
| Distribution | Bull Trout | Juvenile | 0.6890 | |
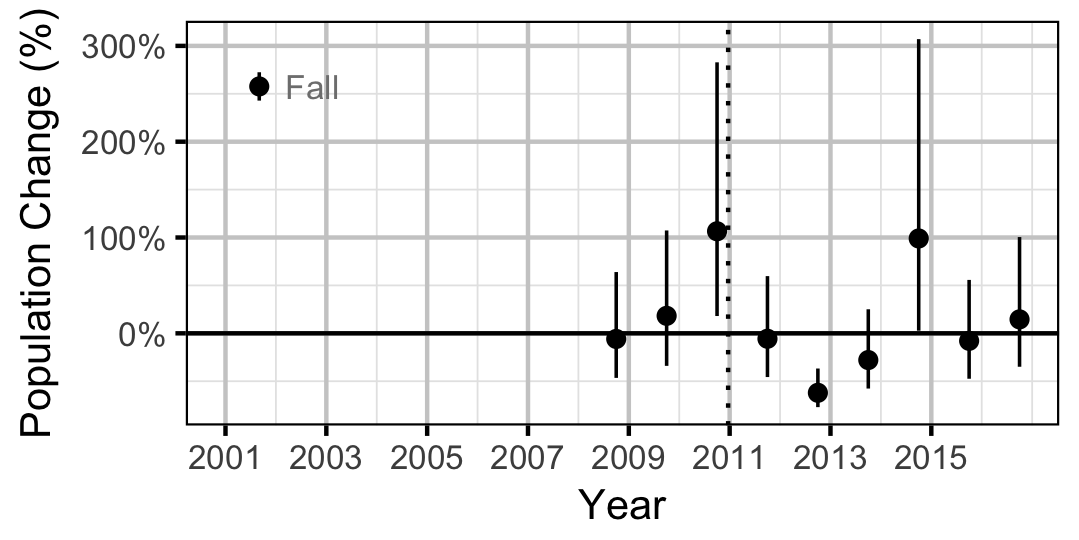
| Growth | Mountain Whitefish | 0.9730 | ||
| Growth | Rainbow Trout | 0.9880 | ||
| Growth | Bull Trout | 0.9860 |
Acknowledgements
The organisations and individuals whose contributions have made this analysis report possible include:
- BC Hydro
- Guy Martel
- Karen Bray
- Jason Watson
- Okanagan National Alliance
- Amy Duncan
- Michael Zimmer
- Charlotte Whitney
- Golder Associates
- David Roscoe
- Dustin Ford
- Sima Usvyatsov
- Dana Schmidt
- Larry Hildebrand
References
Bradford, Michael J, Josh Korman, and Paul S Higgins. 2005. “Using Confidence Intervals to Estimate the Response of Salmon Populations (Oncorhynchus Spp.) to Experimental Habitat Alterations.” Canadian Journal of Fisheries and Aquatic Sciences 62 (12): 2716–26. https://doi.org/10.1139/f05-179.
Fabens, A J. 1965. “Properties and Fitting of the von Bertalanffy Growth Curve.” Growth 29 (3): 265–89.
He, Ji X., James R. Bence, James E. Johnson, David F. Clapp, and Mark P. Ebener. 2008. “Modeling Variation in Mass-Length Relations and Condition Indices of Lake Trout and Chinook Salmon in Lake Huron: A Hierarchical Bayesian Approach.” Transactions of the American Fisheries Society 137 (3): 801–17. https://doi.org/10.1577/T07-012.1.
Kery, Marc. 2010. Introduction to WinBUGS for Ecologists: A Bayesian Approach to Regression, ANOVA, Mixed Models and Related Analyses. Amsterdam; Boston: Elsevier. http://public.eblib.com/EBLPublic/PublicView.do?ptiID=629953.
Kery, Marc, and Michael Schaub. 2011. Bayesian Population Analysis Using WinBUGS : A Hierarchical Perspective. Boston: Academic Press. http://www.vogelwarte.ch/bpa.html.
Plummer, Martyn. 2015. “JAGS Version 4.0.1 User Manual.” http://sourceforge.net/projects/mcmc-jags/files/Manuals/4.x/.
R Core Team. 2016. “R: A Language and Environment for Statistical Computing.” Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
von Bertalanffy, L. 1938. “A Quantitative Theory of Organic Growth (Inquiries on Growth Laws Ii).” Human Biology 10: 181–213.