Background
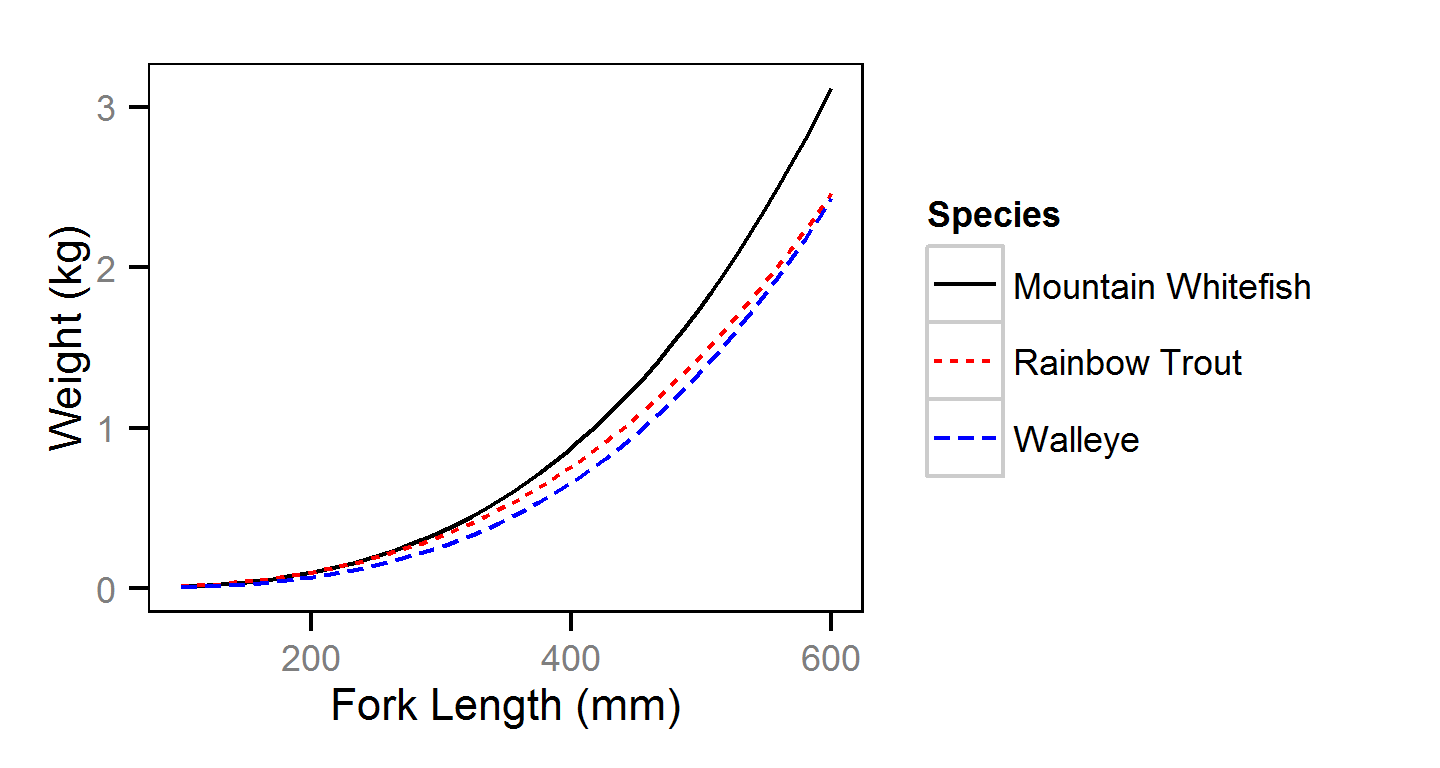
In the mid 1990s BC Hydro began operating Hugh L. Keenleyside (HLK) Dam to reduce
dewatering of Mountain Whitefish and Rainbow Trout eggs.
The primary goal of the Lower Columbia River Fish Population Indexing program is to answer
two key management questions:
What are the abundance, growth rate, survival rate, body condition, age distribution, and spatial distribution of subadult and adult Whitefish, Rainbow Trout, and Walleye in the LCR?
What is the effect of inter-annual variability in the Whitefish and Rainbow Trout flow regimes on the abundance, growth rate, survival rate, body condition, and spatial distribution of subadult and adult Whitefish, Rainbow Trout, and Walleye in the LCR?
Methods
Data Preparation
The fish indexing data were provided by Golder Associates in the form of
an Access database. The discharge and temperature data were queried from a BC Hydro database maintained by Poisson Consulting.
The data were prepared for analysis
using R version 3.1.0 (Team (2013)).
Statistical Analysis
Hierarchical Bayesian models were fitted to the fish indexing data data using
R version 3.1.0 (Team (2013))
and JAGS 3.4.0 (Plummer (2012))
which interfaced with each other via
jaggernaut 1.8.2 (Thorley (2014)).
For additional information on hierarchical Bayesian modelling in the BUGS language, of which JAGS uses a dialect, the reader is referred to Kery and Schaub (2011) pages 41-44.
Unless specified, the models assumed vague (low information) prior distributions
(Kéry and Schaub (2011)36). The posterior distributions were estimated from a minimum of 1,000 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of three chains (Kéry and Schaub (2011)38-40).
Model convergence was confirmed by ensuring that Rhat (Kéry and Schaub (2011)40) was less than 1.1 for each of the parameters in the model (Kéry and Schaub (2011)61).
Model adequacy was confirmed by examination of residual plots.
The posterior distributions of the fixed
(Kéry and Schaub (2011)75) parameters
are summarised in terms of a point estimate (mean),
lower and upper 95% credible limits (2.5th
and 97.5th percentiles), the standard deviation (SD), percent relative error (half the 95% credible interval as a percent of the point estimate) and significance (Kéry and Schaub (2011)37,42).
Variable selection was achieved by dropping uninformative explanatory
variables where a variable was considered to be uninformative if its
percent relative error was \(\geq\) 100%. In the case of fixed effects
this is approximately equivalent to dropping insignificant variables, i.e., those with a significance \(\geq\) 0.05.
The results are displayed
graphically by plotting the modeled relationships between particular
variables and the response with 95%
credible intervals (CRIs) with the
remaining variables held constant. In general,
continuous and discrete fixed variables are held constant at their mean and
first level values respectively while random variables are held constant at their
typical values (expected values of the underlying hyperdistributions)
(Kéry and Schaub (2011)77-82). Where informative the influence of particular variables is expressed in terms
of the effect size (i.e., percent change in the response variable) with
95% CRIs
(Bradford et al. (2005)). Plots were produced using the ggplot2 R package (Wickham (2009)).
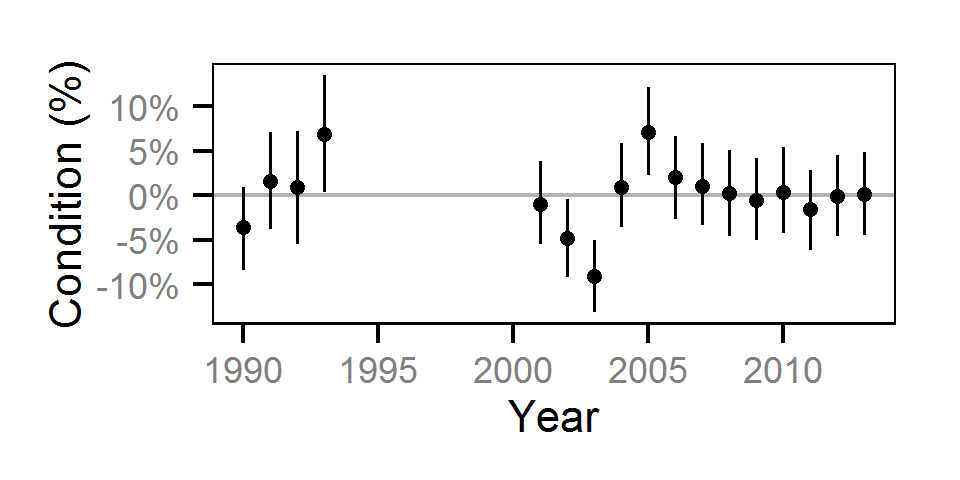
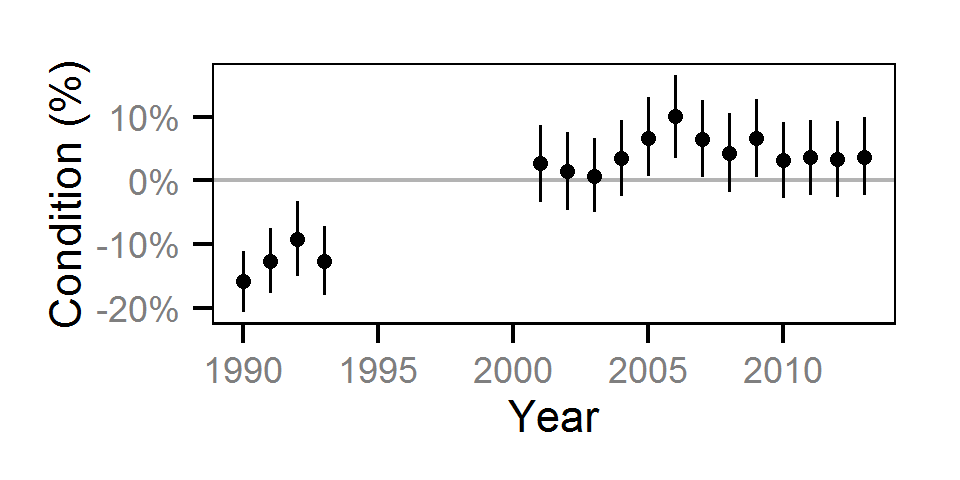
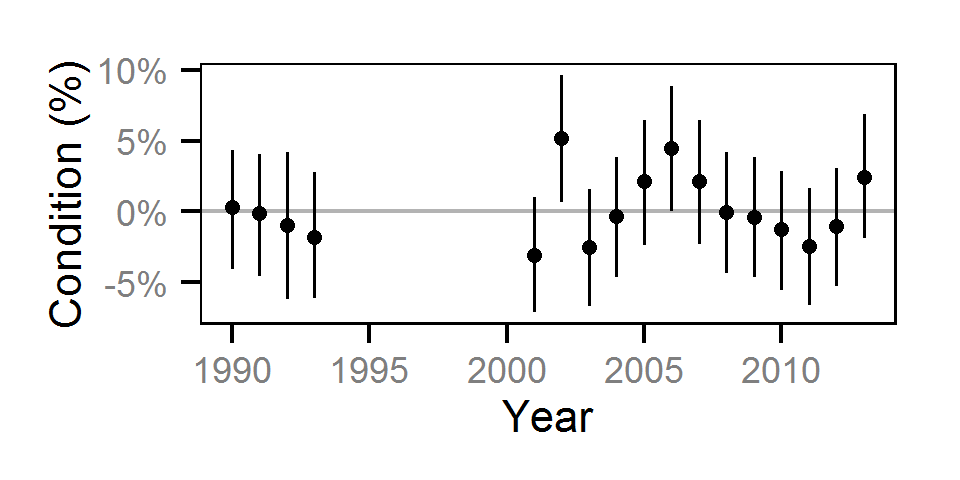
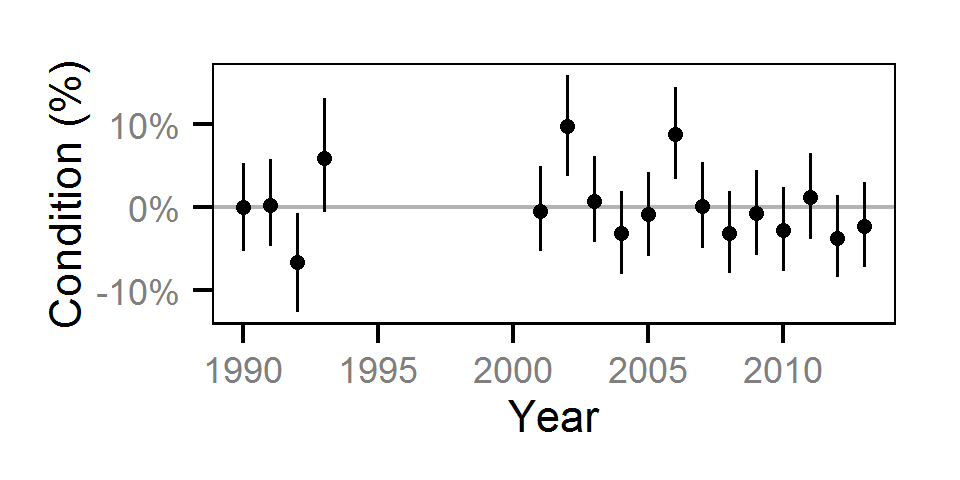
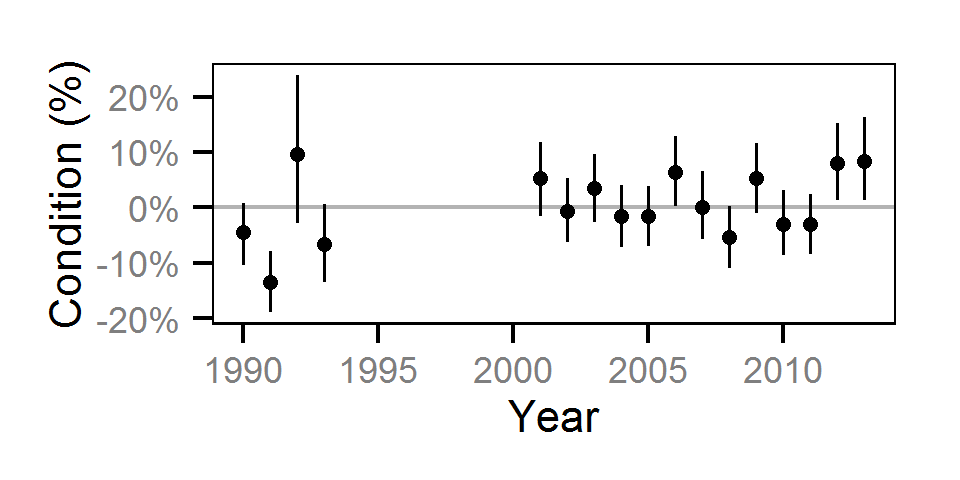
Condition
Condition was estimated via
an analysis of weight-length relations (He et al. (2008)).
Key assumptions of the condition model include:
- Weight varies with length and date.
- Weight varies randomly with year.
- The relationship between length and weight varies with date.
- The relationship between length and weight varies randomly with year.
- The effect of year on weight is correlated with the effect of year on the relationship between length and weight.
- The residual weight variation in weight is log-normally distributed.
Only previously untagged fish were included in models to avoid potential effects of tagging on body condition.
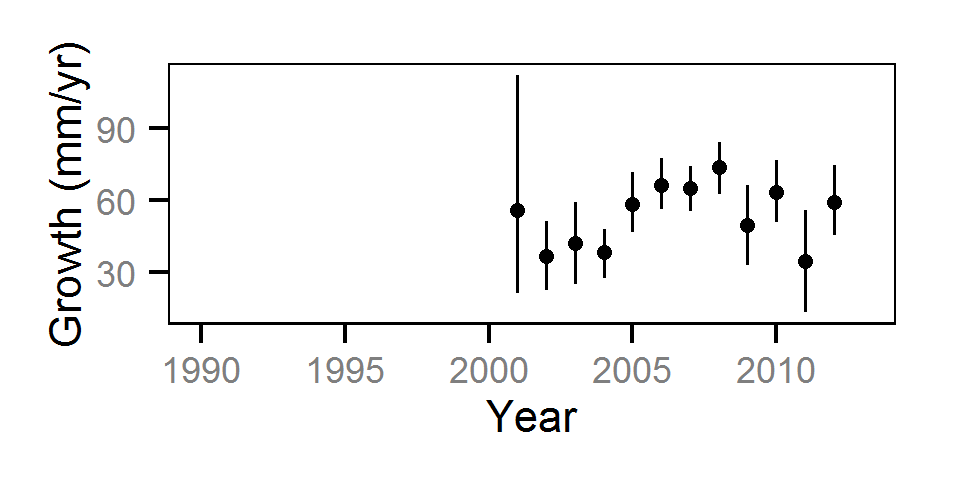
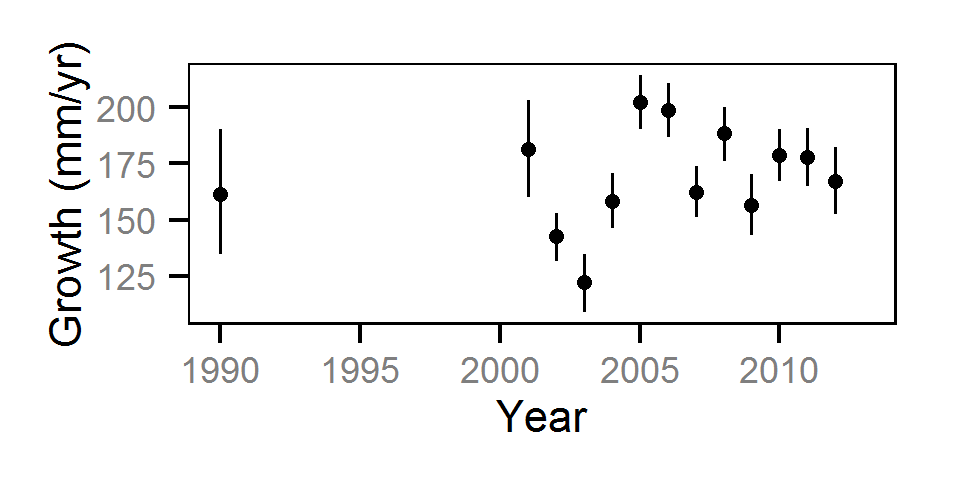
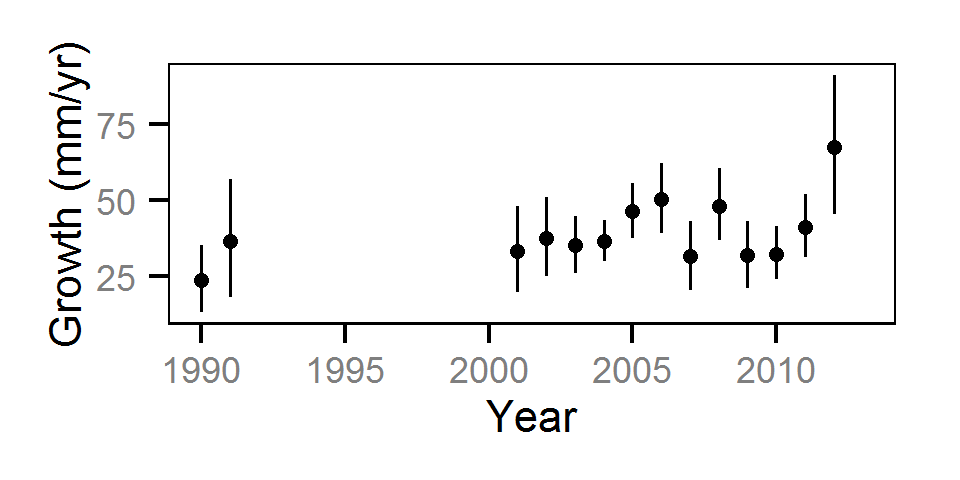
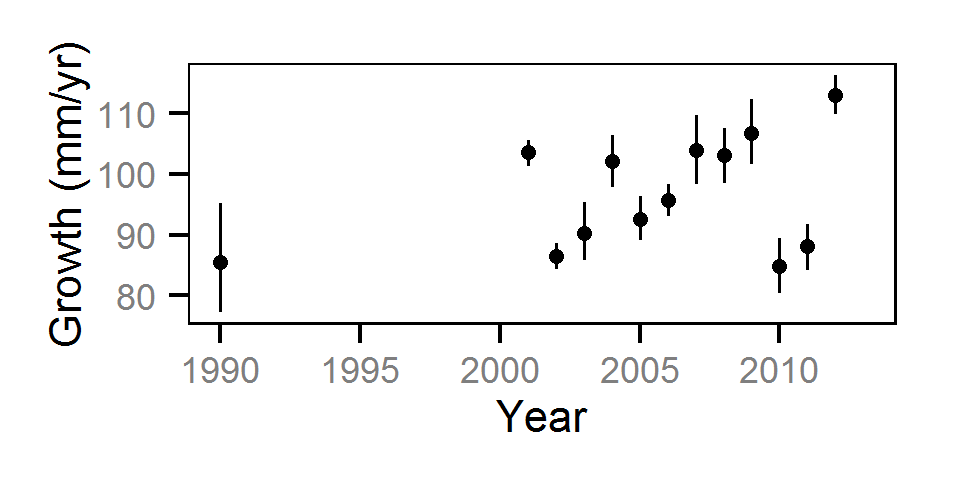
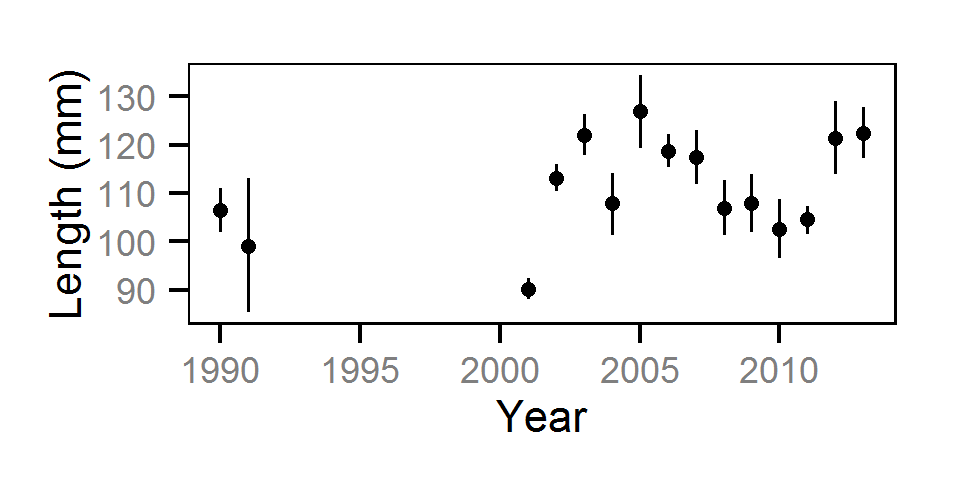
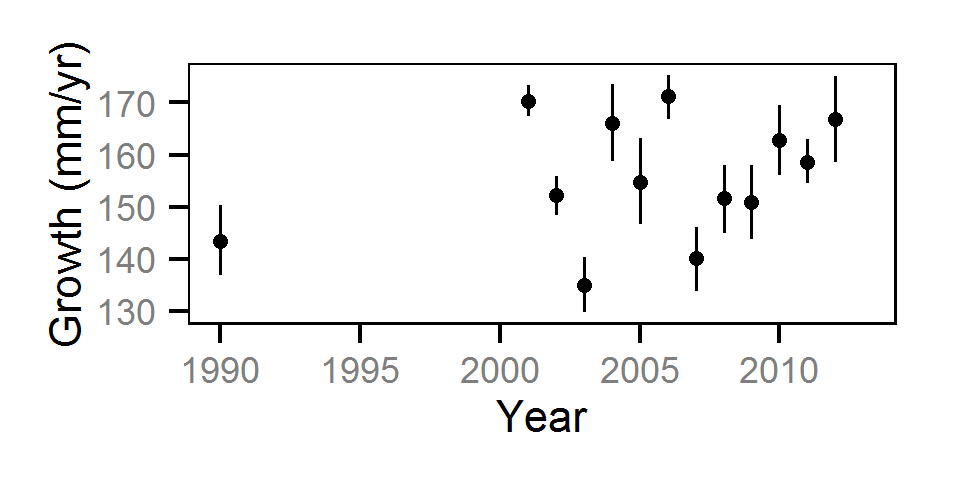
Growth
Annual growth was estimated from the inter-annual recaptures
using the Fabens method (Fabens (1965)) for estimating the von Bertalanffy growth curve (Bertalanffy (1938)).
Key assumptions of the growth model include:
- The growth coefficient (k) varies randomly with year.
- The residual growth variation is normally distributed.
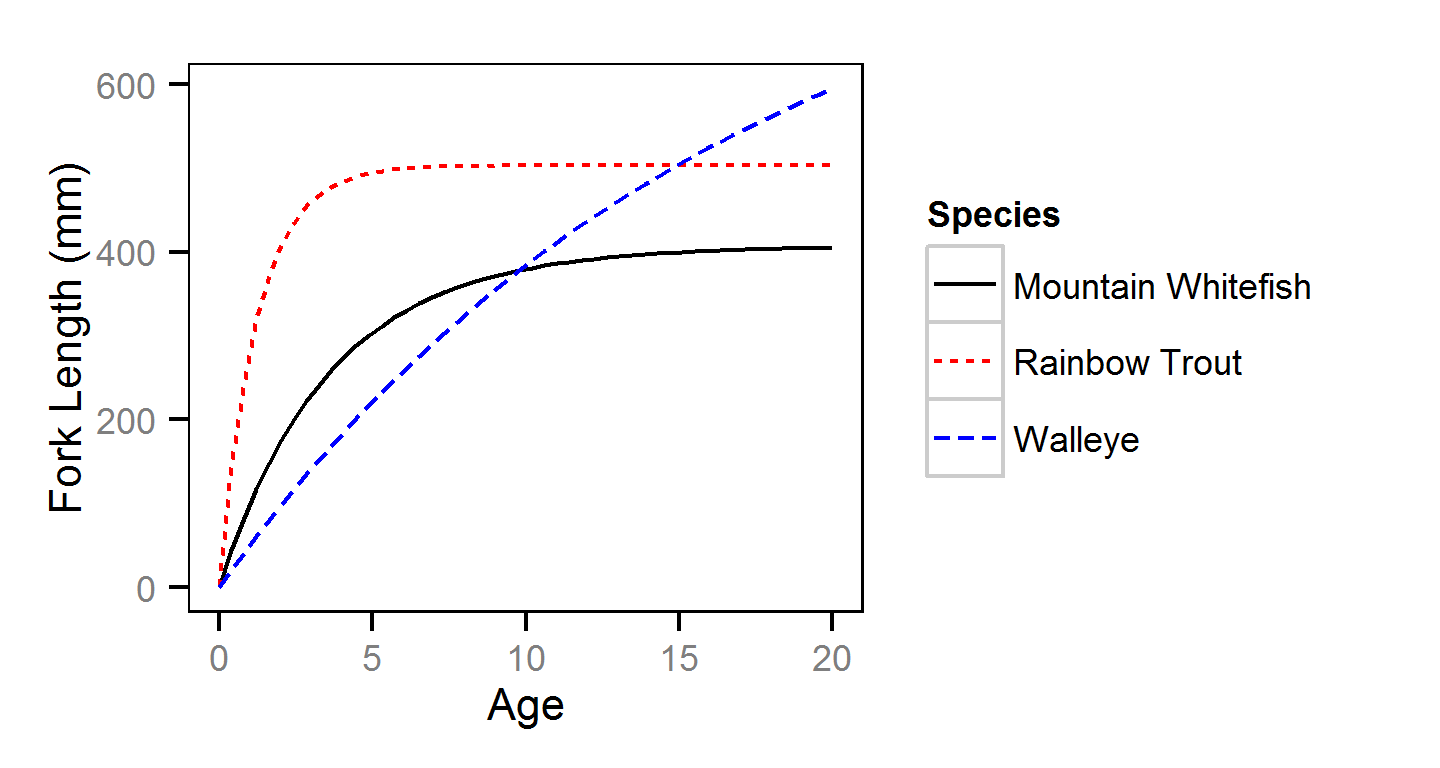
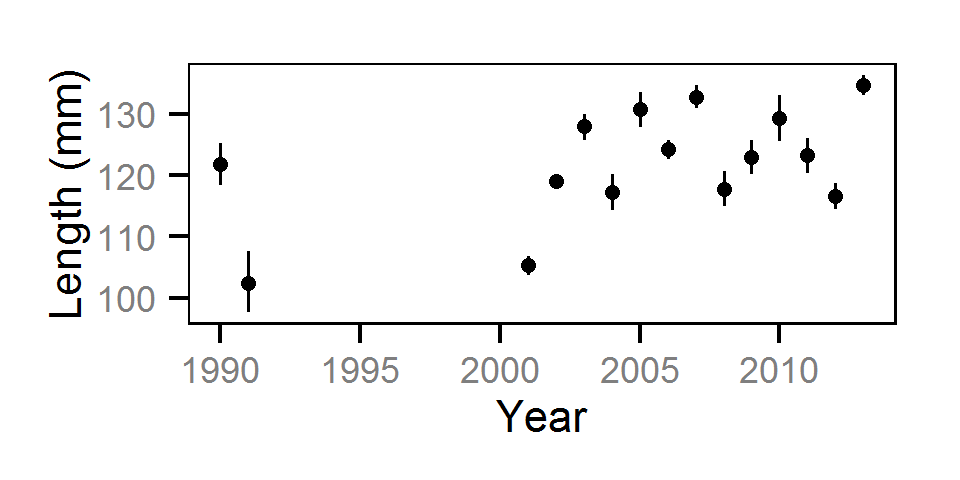
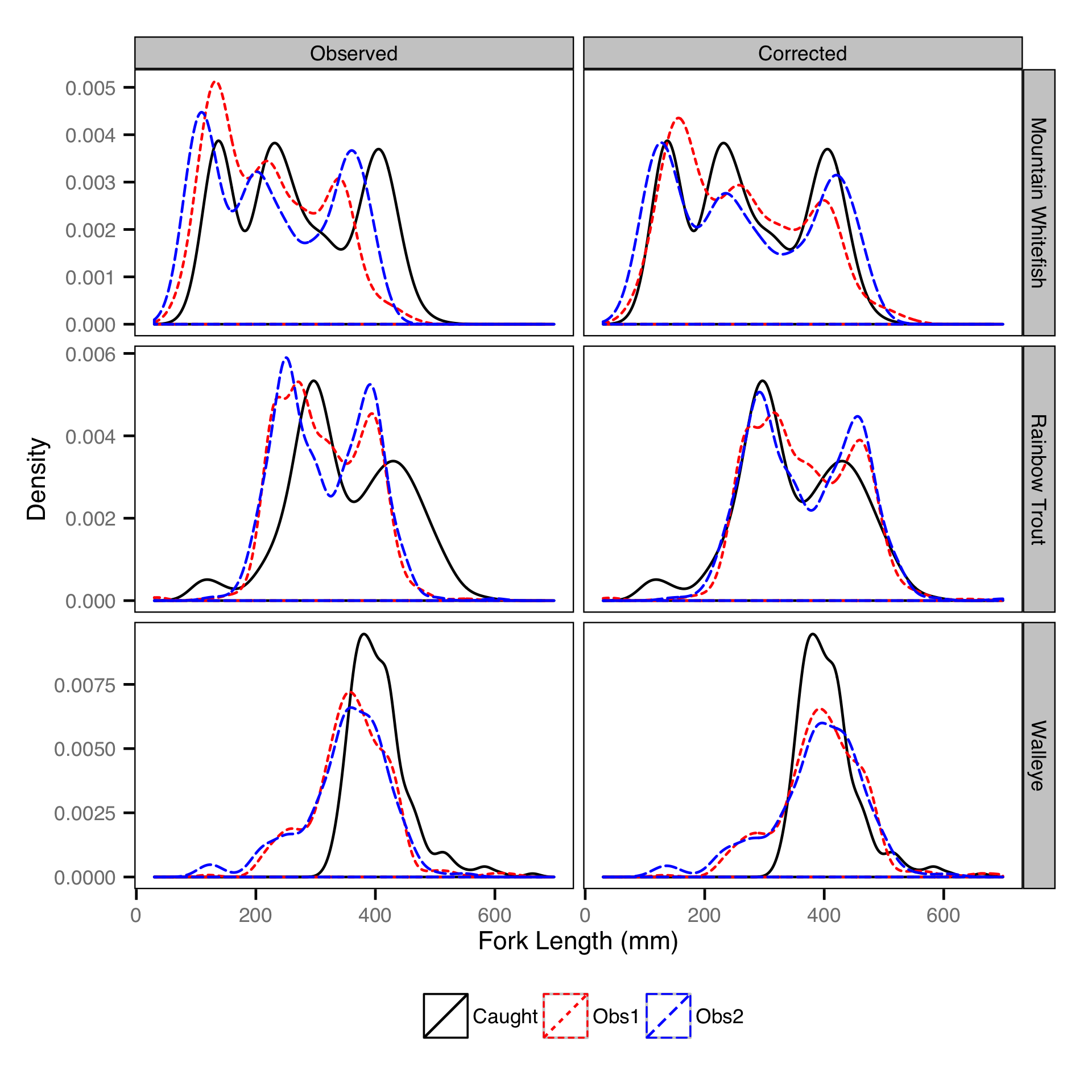
Length-At-Age
The length-at-age of Mountain Whitefish and Rainbow Trout was estimated from
the annual length-frequency distributions using a finite mixture distribution
model (MacDonald and Pitcher 1979).
Key assumptions of the length-at-age model include:
- There are three distinguishable age-classes for each species: age-0, age-1 and age-2 and older. - Length increases with age-class.
- Length varies as a second-order polynomial of date;
- Length varies randomly by year within age-class.
- The proportion of individuals belonging to each age-class remained constant among years.
- Individual variation in length is normally distributed.
The model was used to estimate the cut-offs between age-0, age-1 and age-2 and older individuals by year. For the purposes of estimating other population parameters by life stage, age-0 individuals were classified as fry, age-1 individuals were classified as subadult, and age-2 and older individuals were classified as adult. Walleye could not be separated by life stage due to a lack of discrete modes in the length-frequency distributions for this species. Consequently, all captured Walleye were considered to be adults.
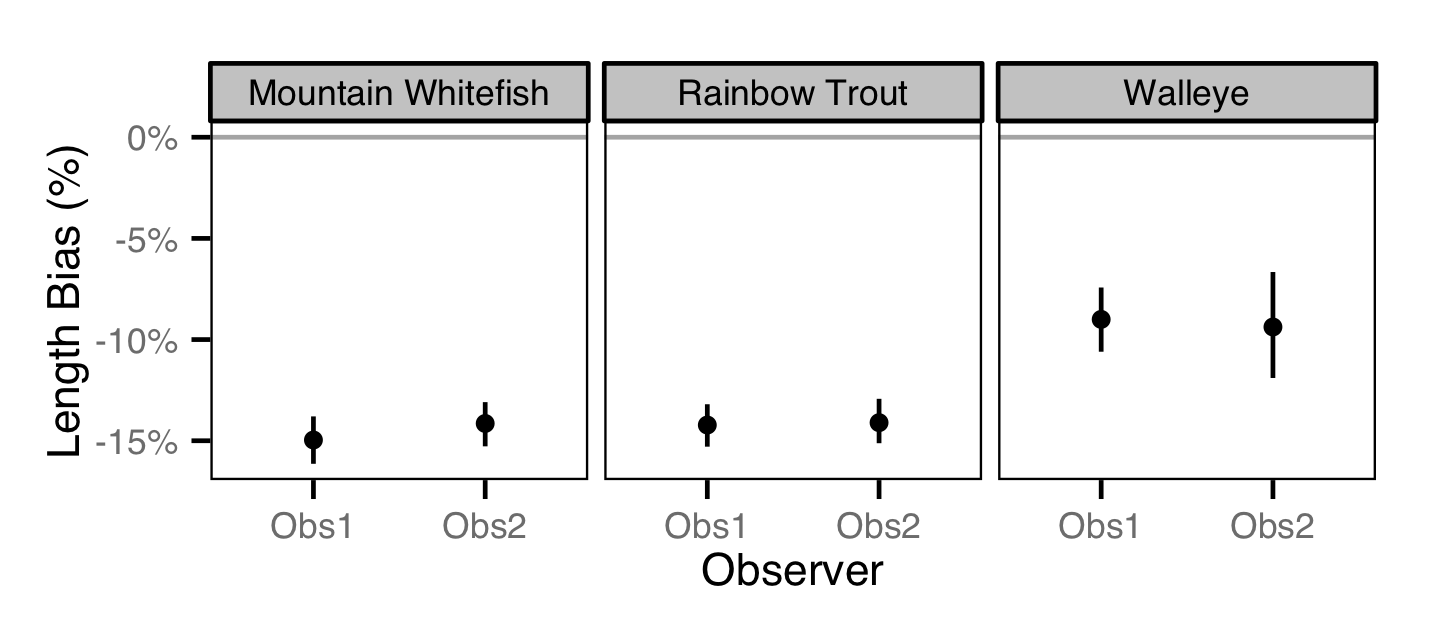
Length Bias
The bias in observer’s fish length estimates was quantified using a model with a categorical distribution
that compared the proportions of fish in different length-classes for each observer in 2013 to the equivalent proportions for the measured fish.
Key assumptions of the length bias model include:
- The percent bias varies by observer.
- The percent bias is constant by fish length.
The observer’s fish lengths were corrected for the estimated bias before being
classified as fry, subadult and adult based on the length-at-age cutoffs.
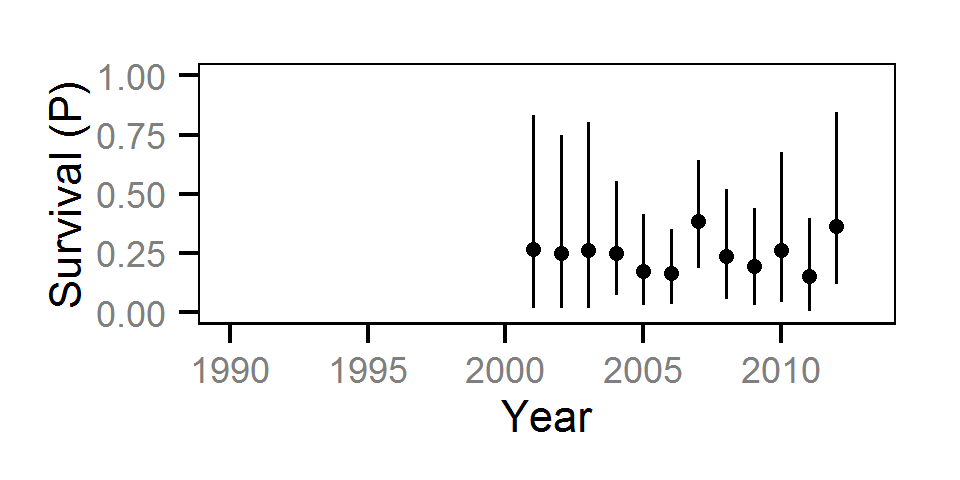
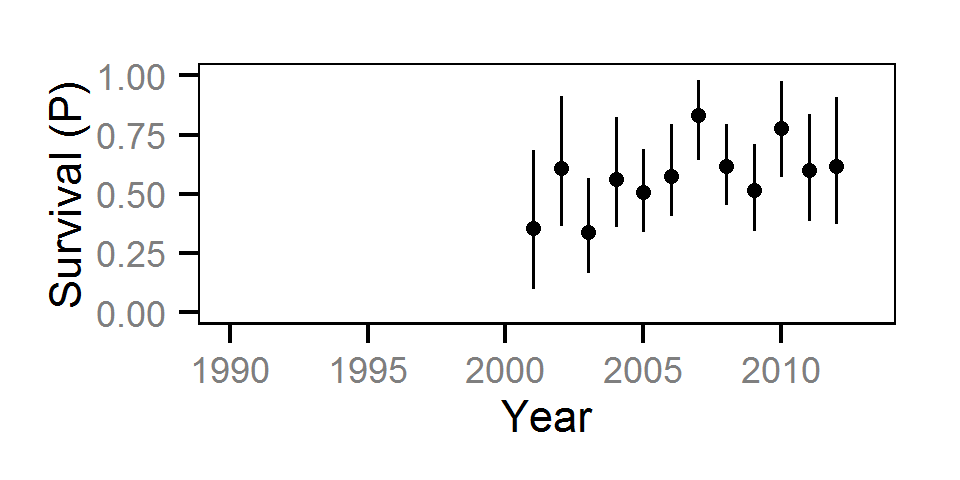
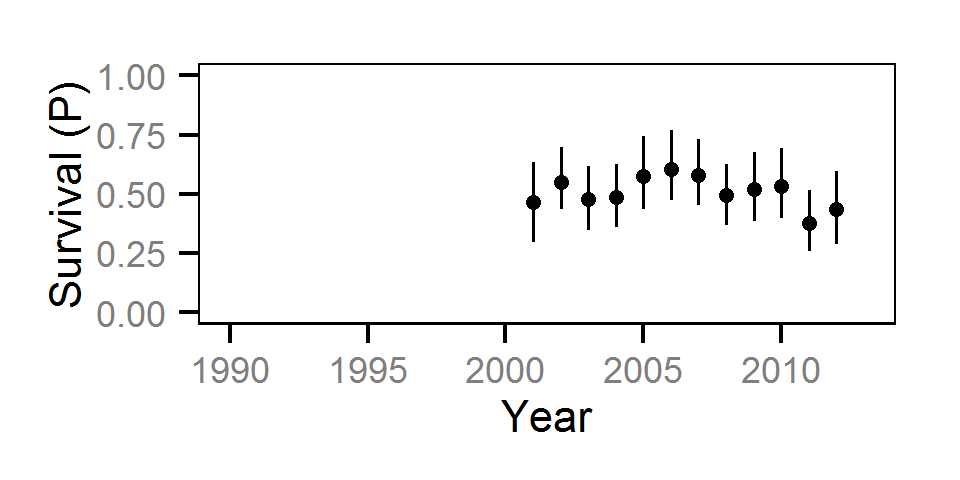
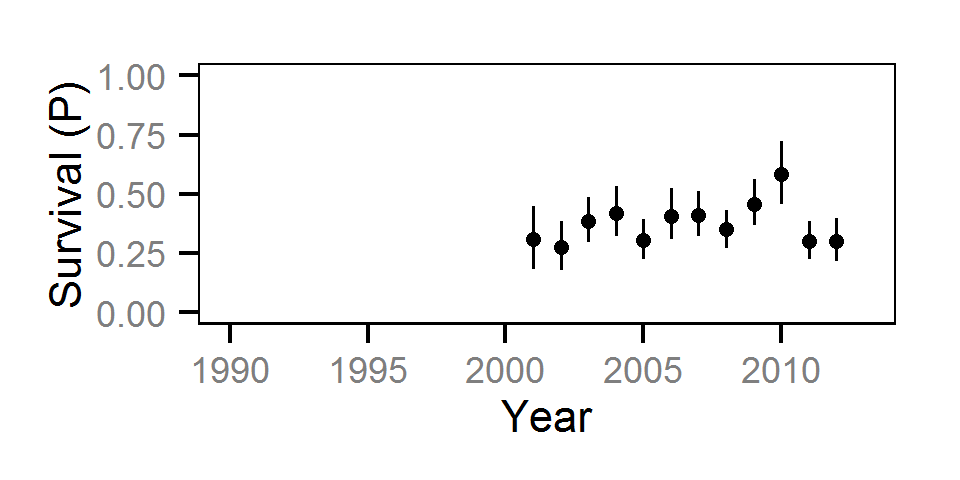
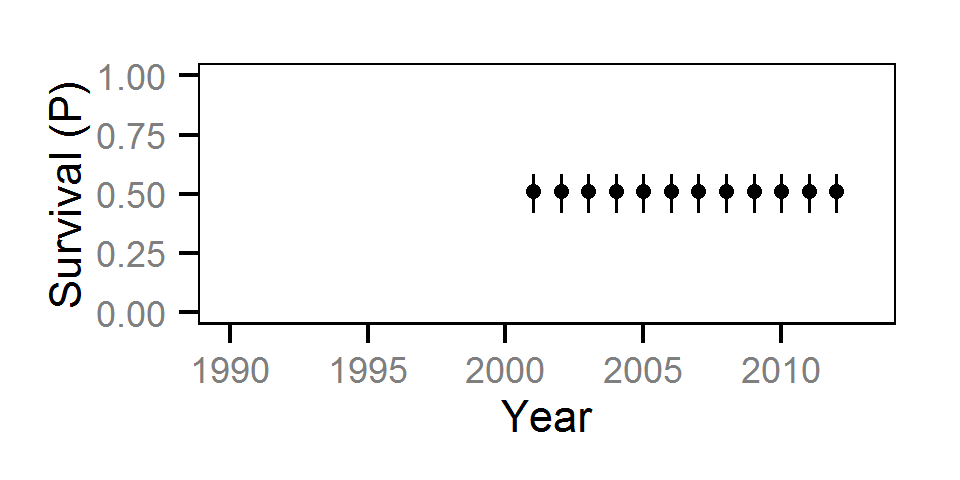
Survival
The annual survival rate was estimated by fitting a Cormack-Jolly-Seber model (Kéry and Schaub (2011)172-177) to inter-annual recaptures.
Key assumptions of the survival model include:
- Survival varies randomly with year within life stage.
- The encounter probability is constant across years.
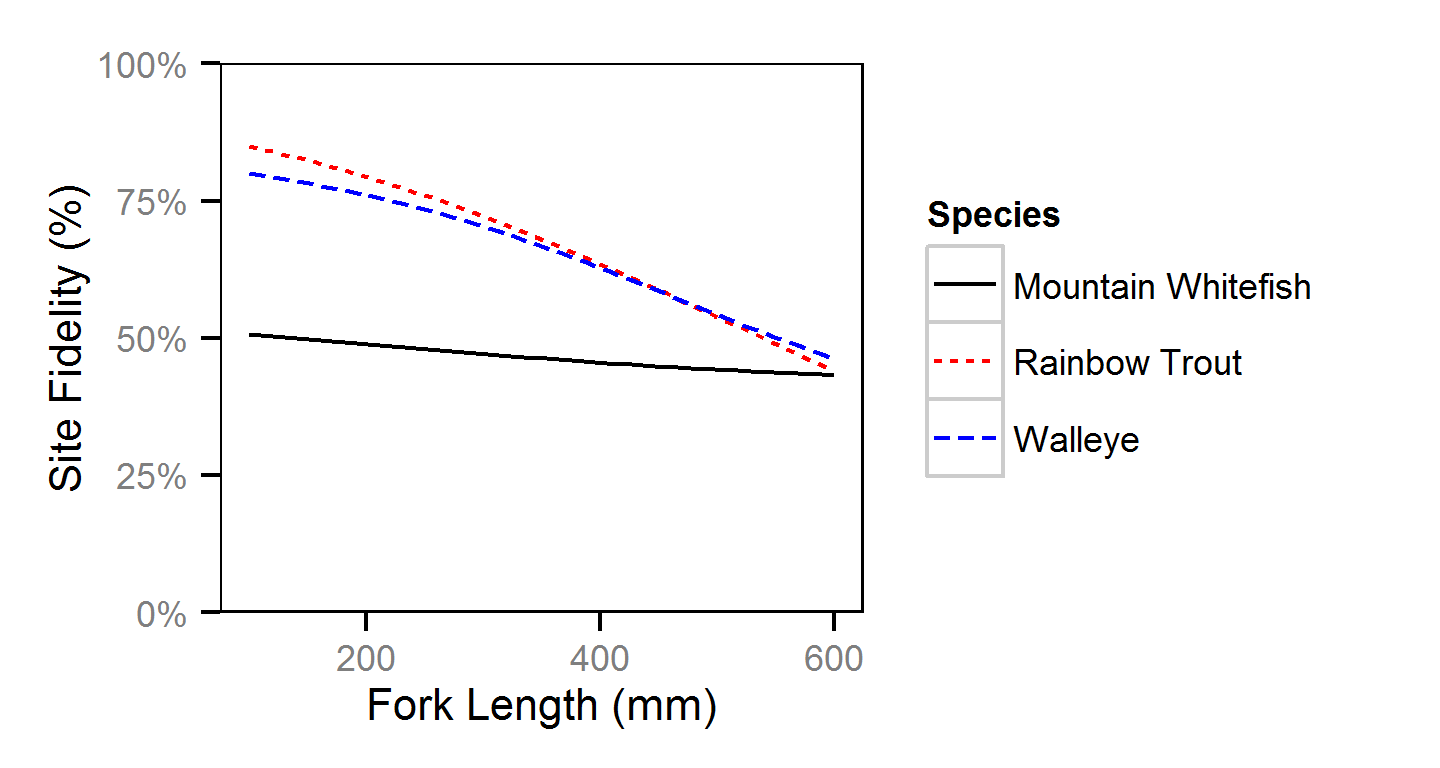
Site Fidelity
The probability of a recaptured fish being caught at the same site at which it was previously encountered versus a different site (the site fidelity)
was estimated using a logistic regression.
Key assumptions of the site fidelity model include:
- The site fidelity varies with body length.
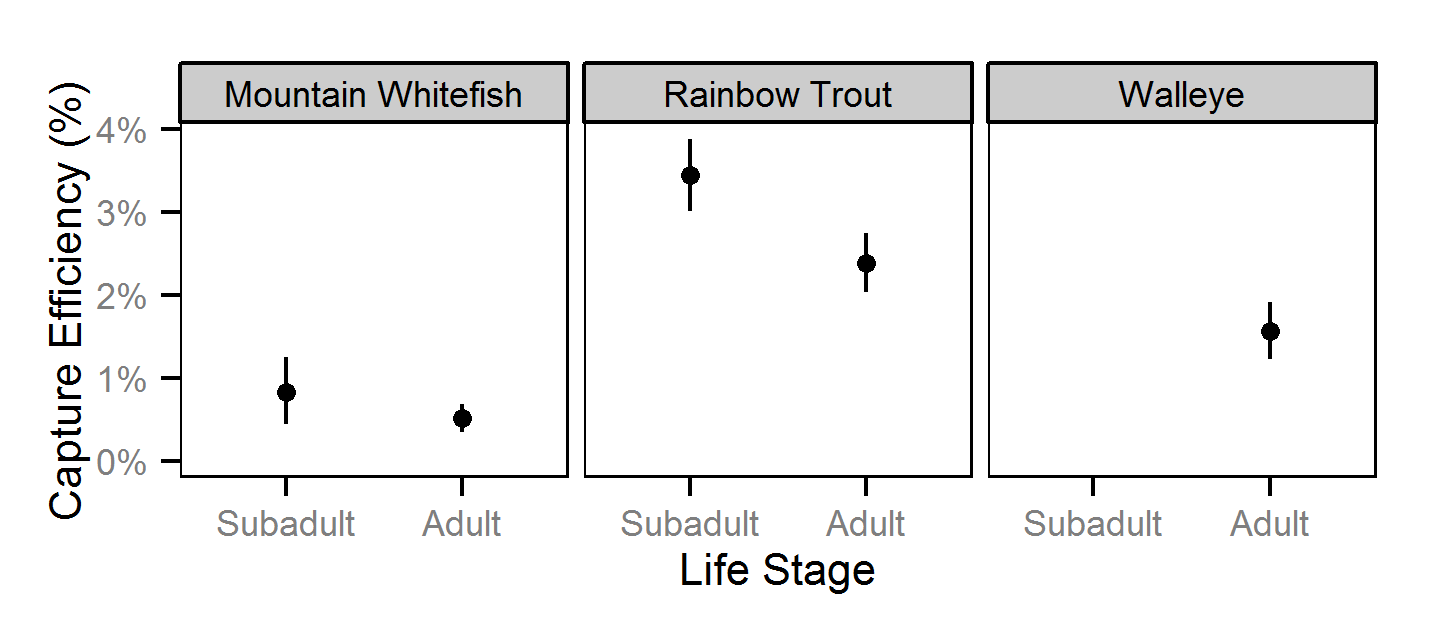
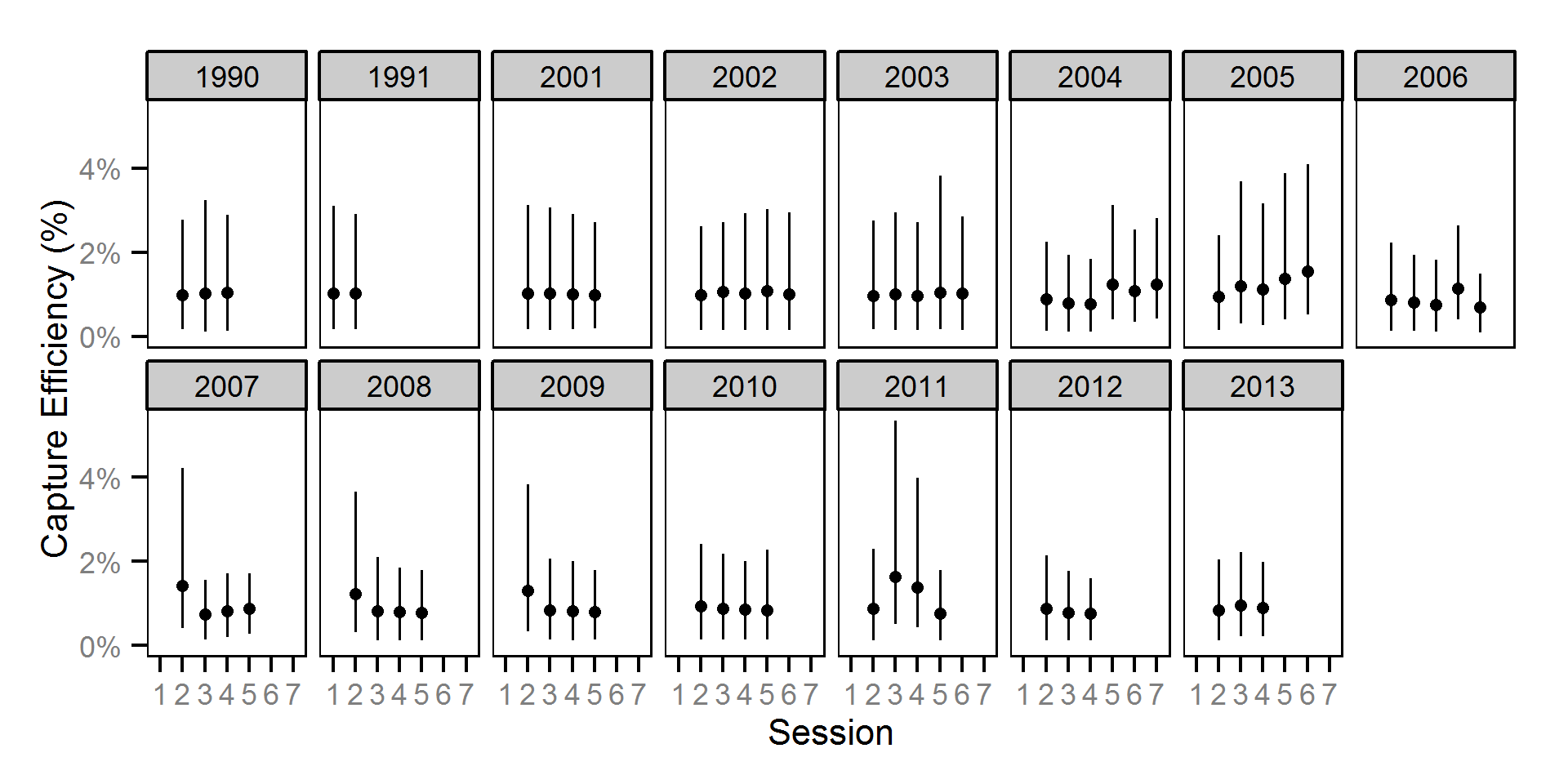
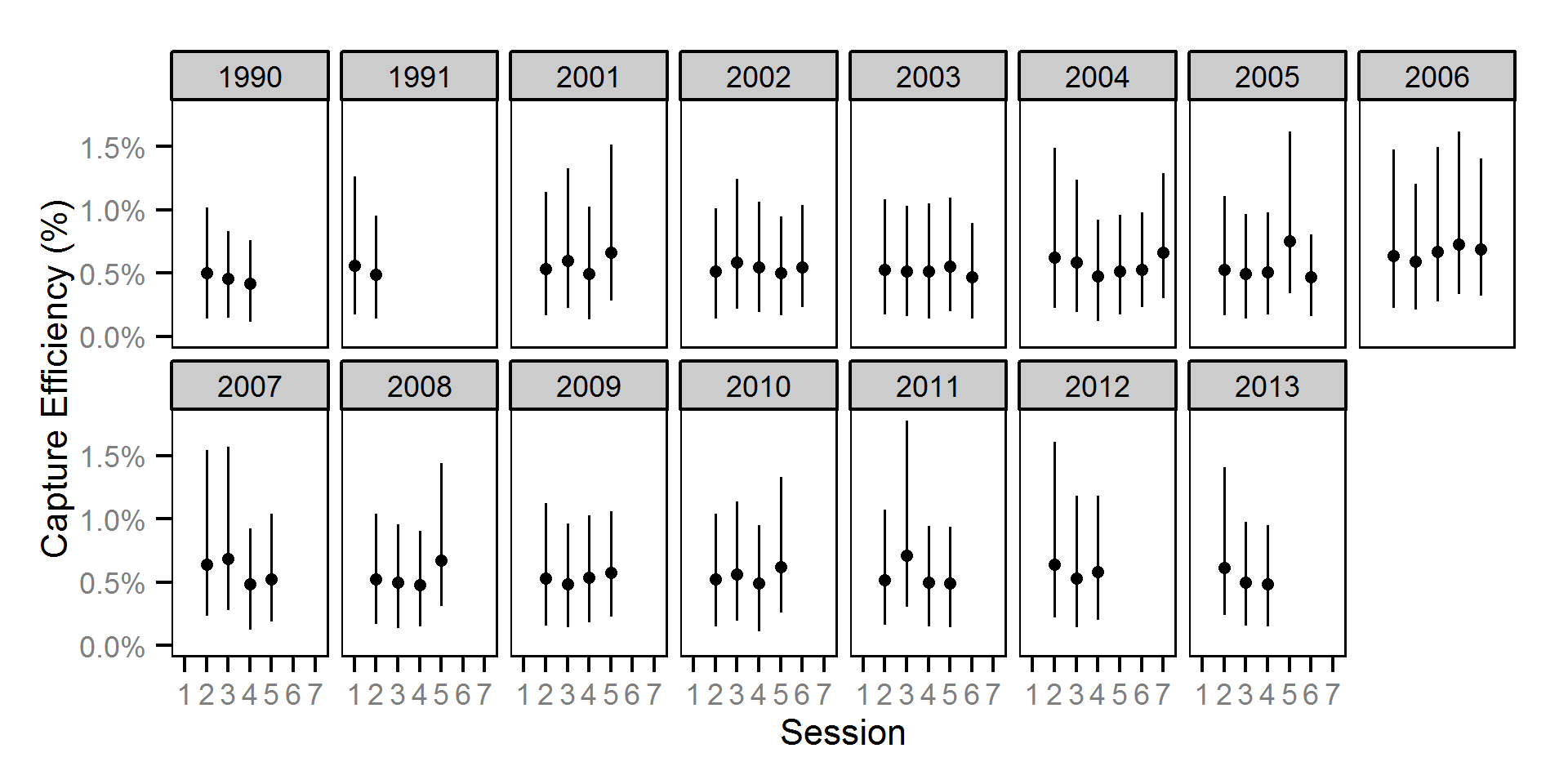
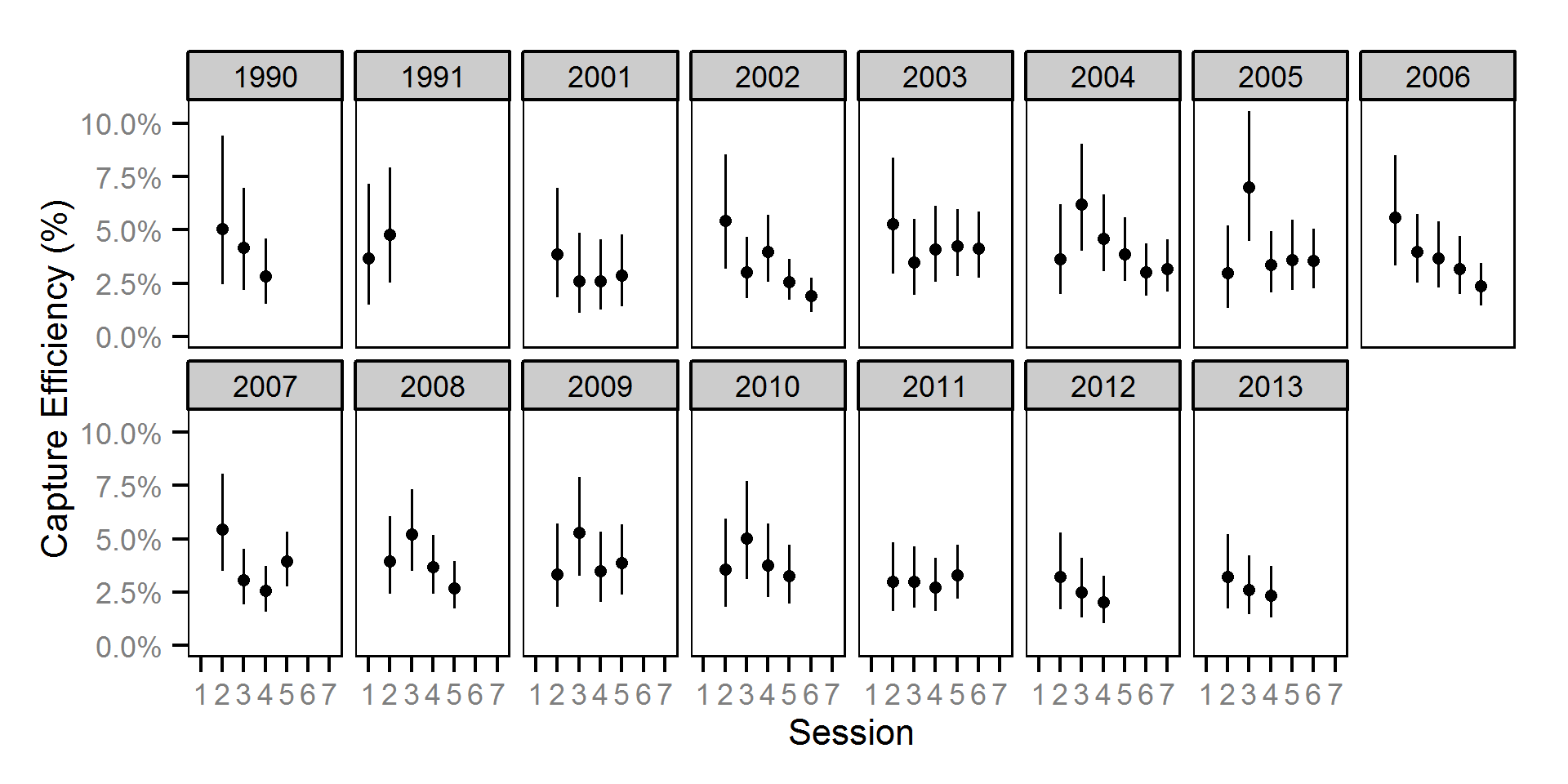
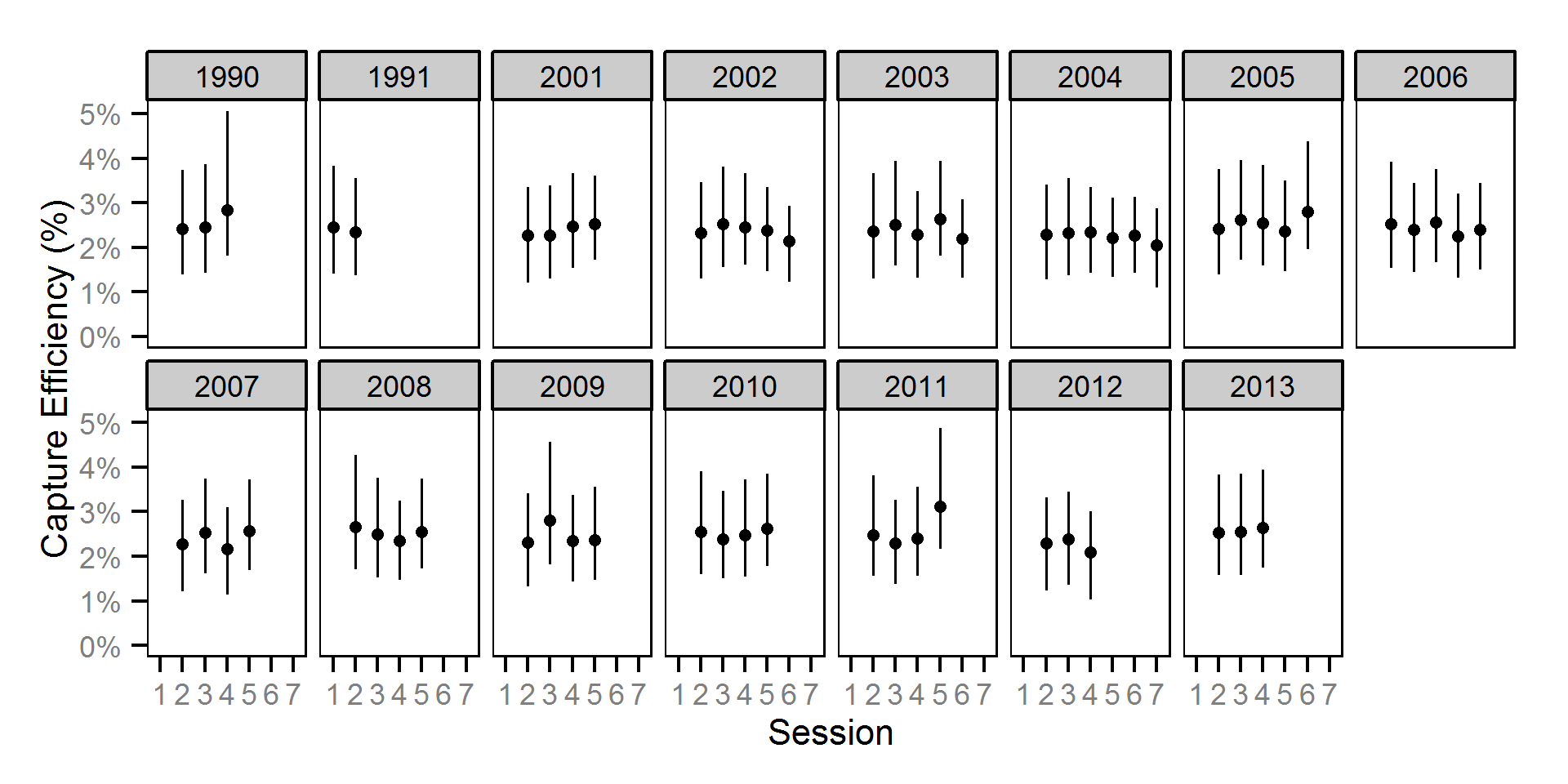
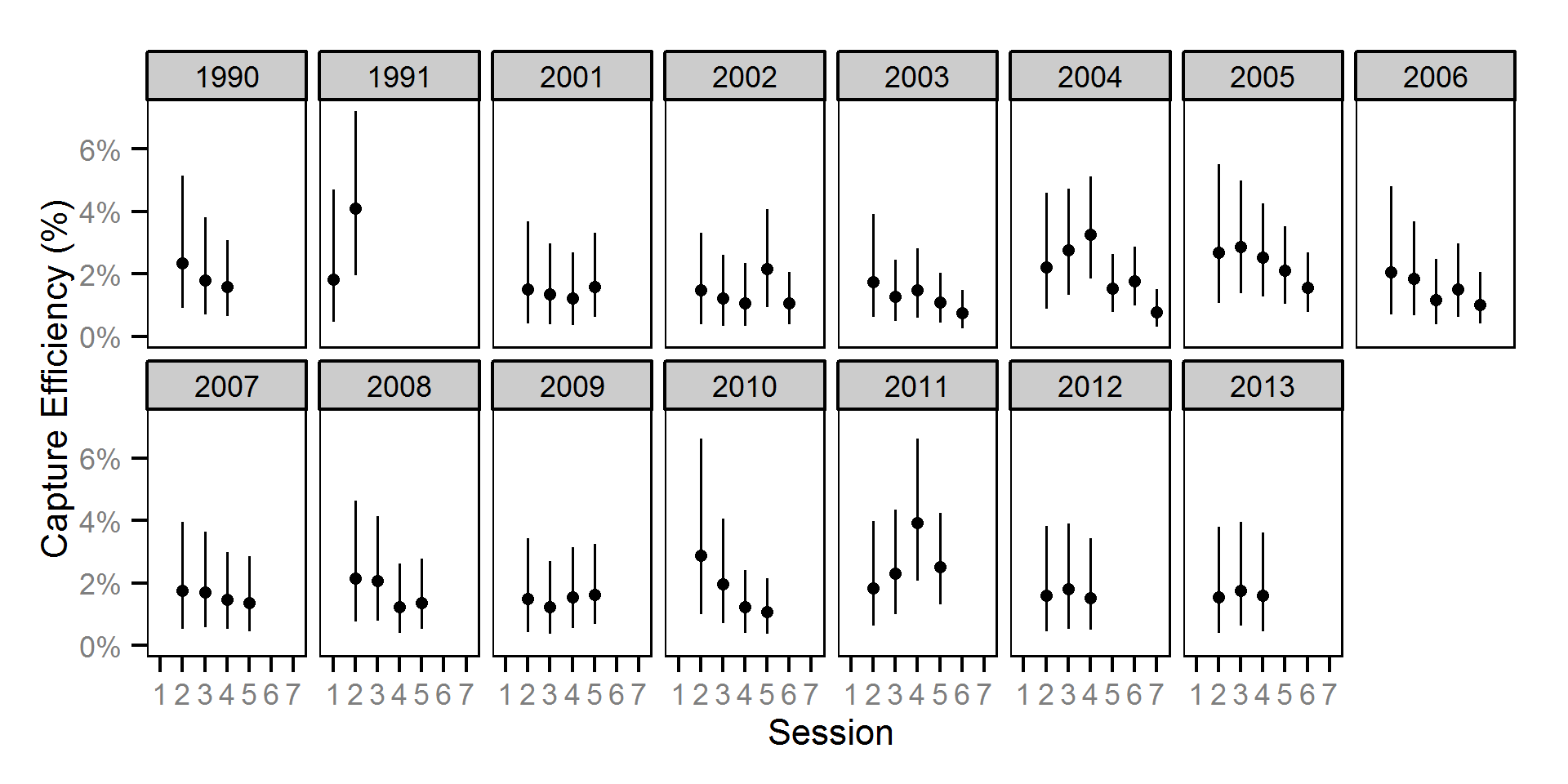
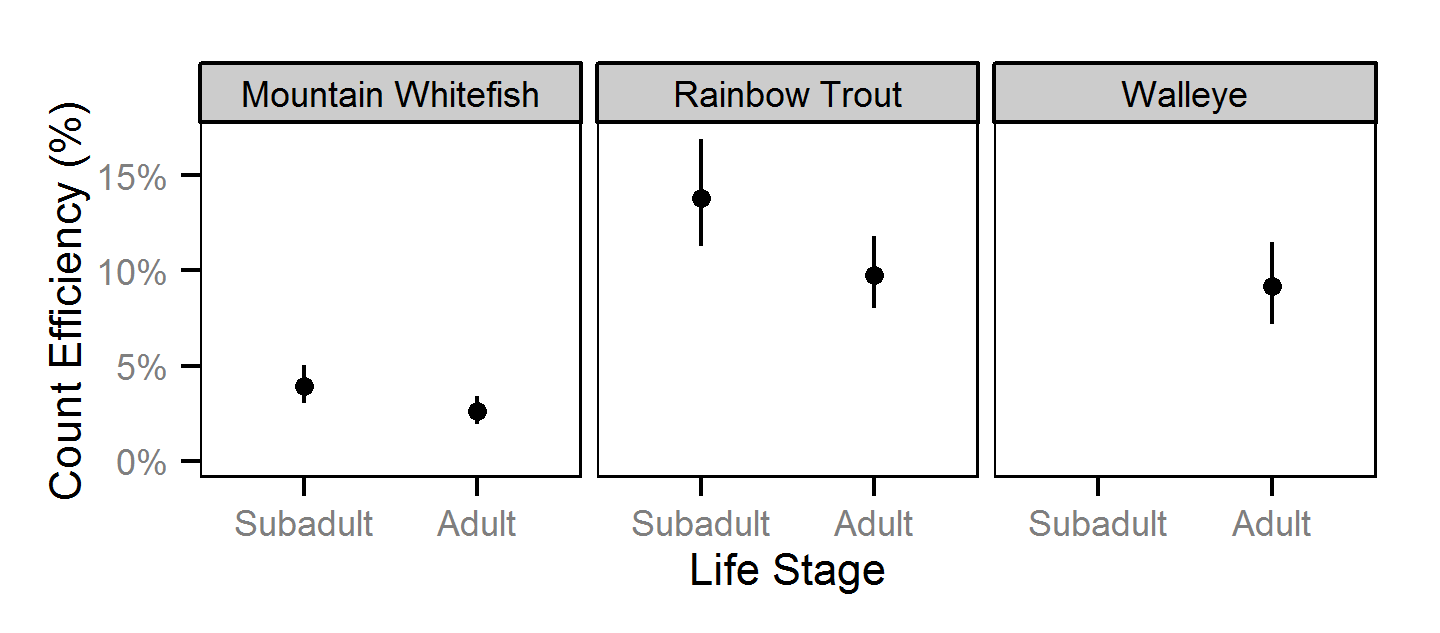
Capture Efficiency
The probability of capture was estimated using a recapture-based binomial model (Kéry and Schaub (2011)134-136, 384-388).
Key assumptions of the capture efficiency model include:
- The capture probability varies randomly by session within year.
- The probability of a marked fish remaining at a site is the estimated site fidelity.
- The number of recaptures is described by a binomial distribution.
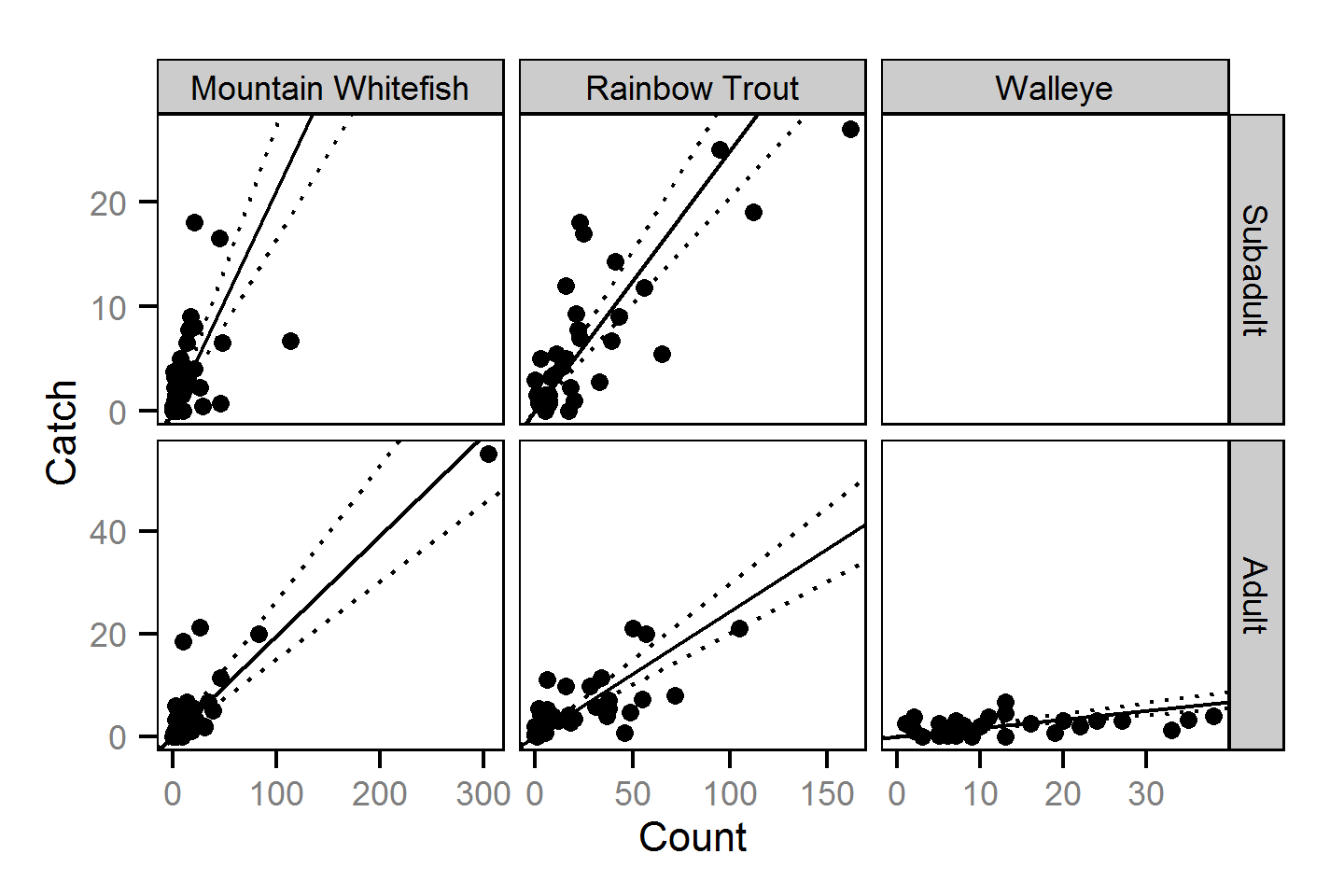
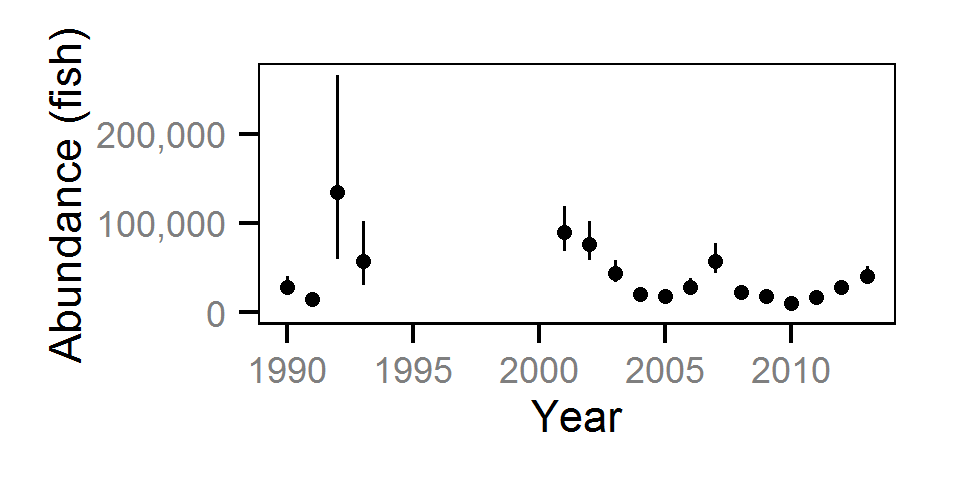
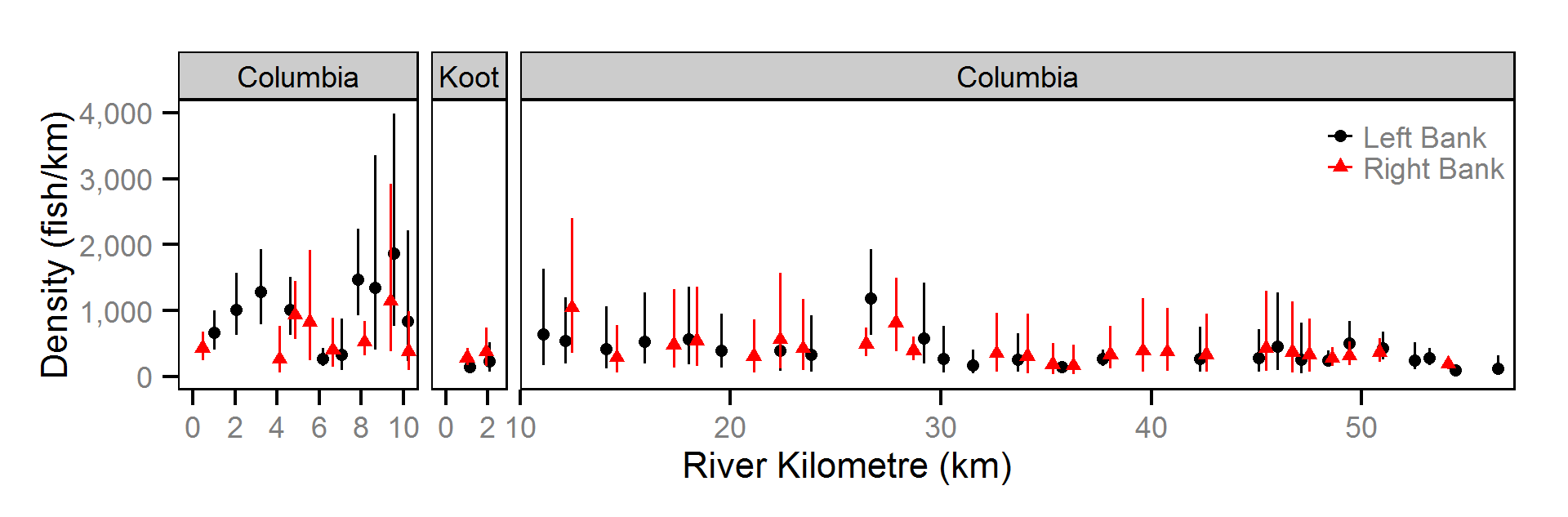
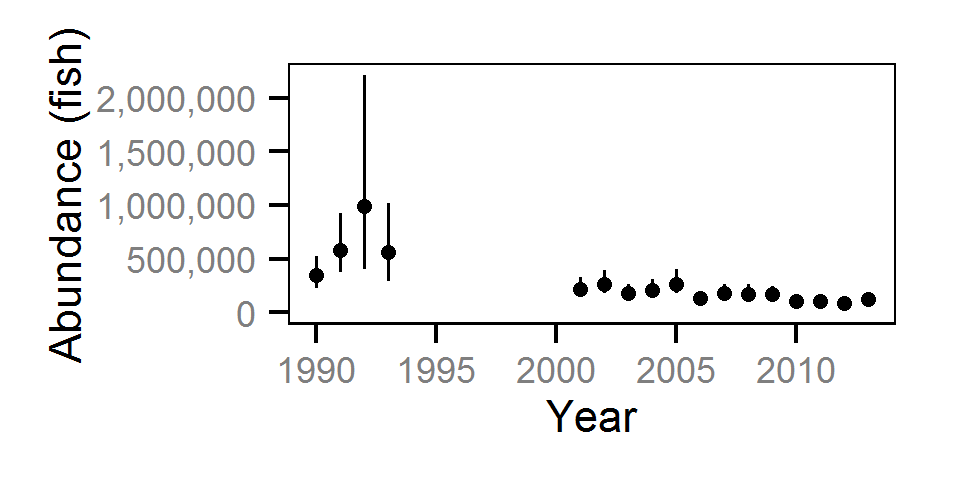
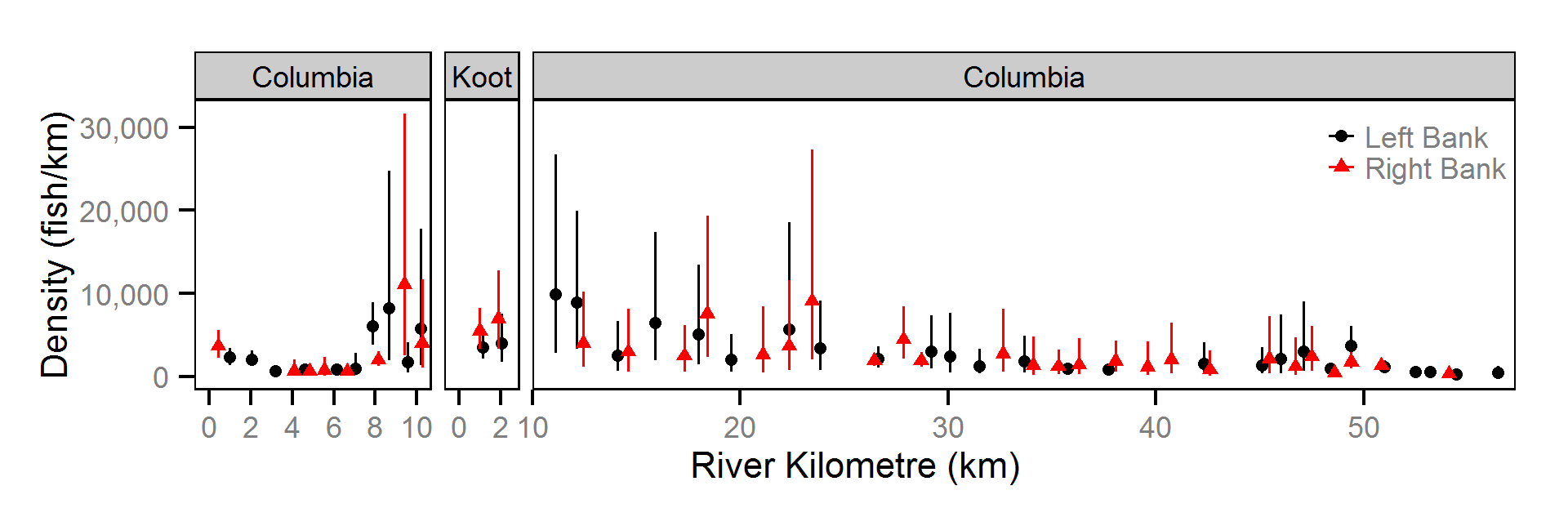
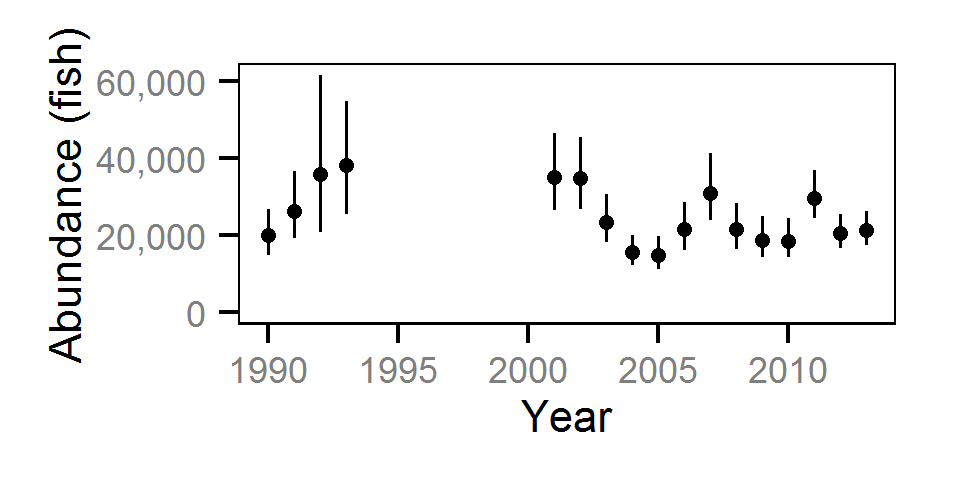
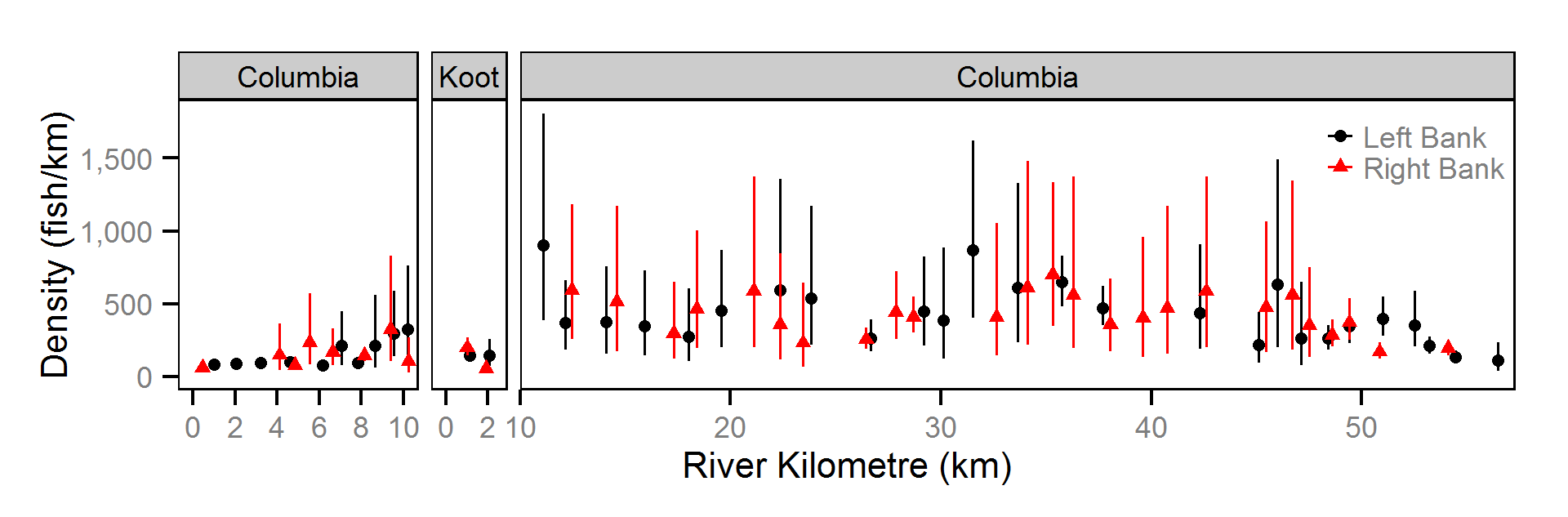
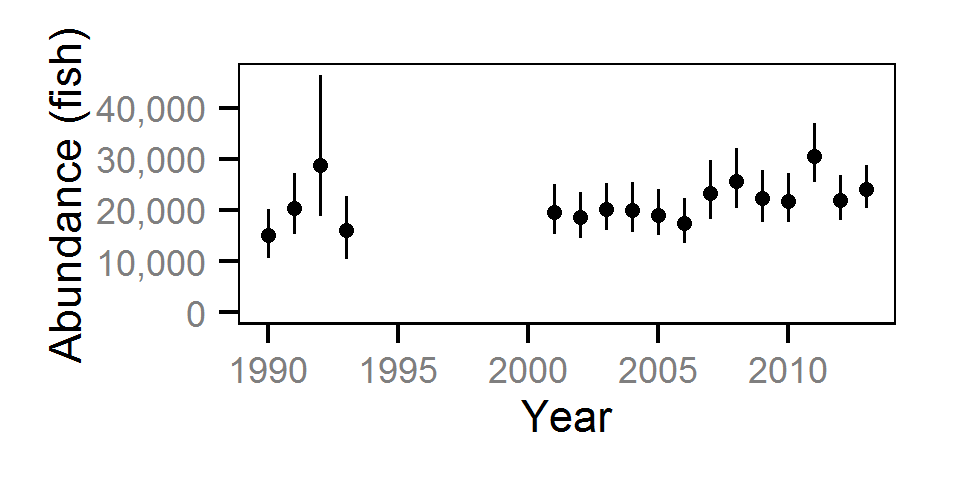
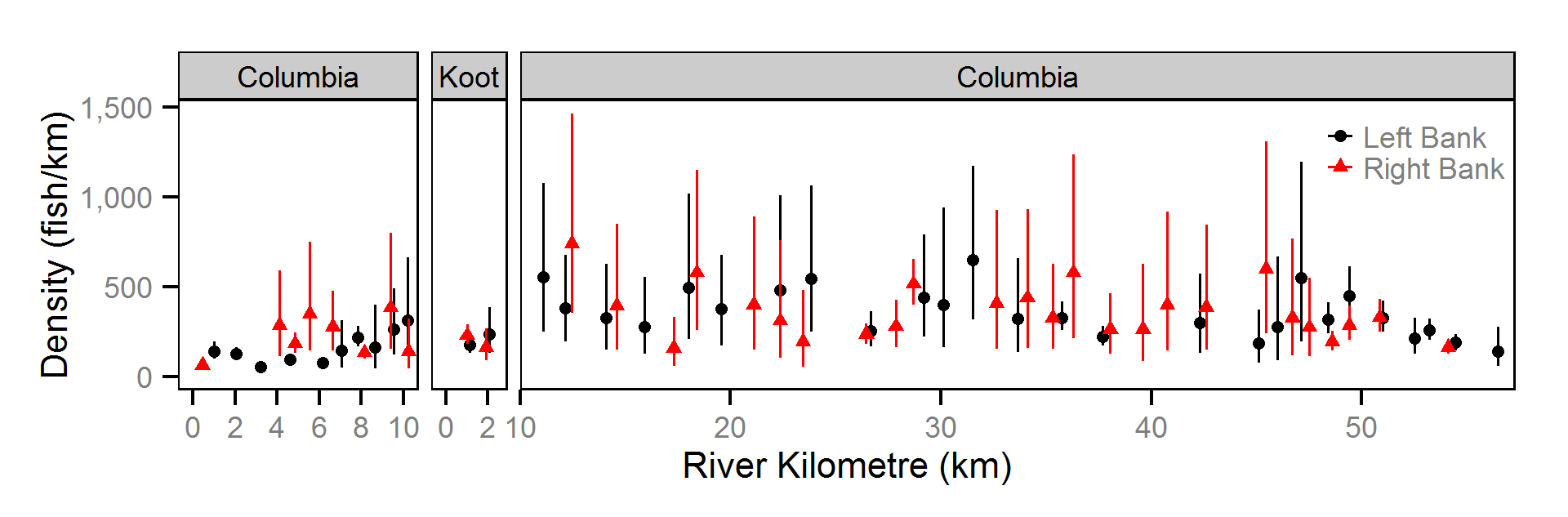
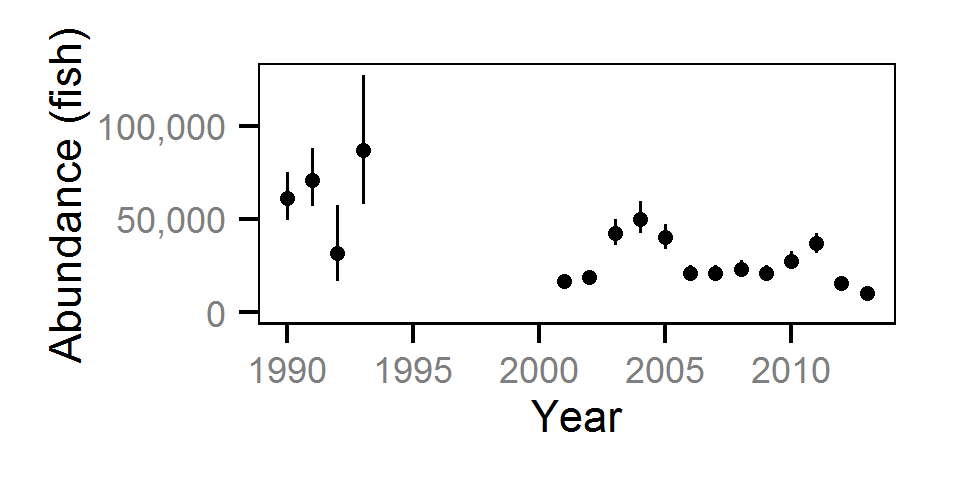
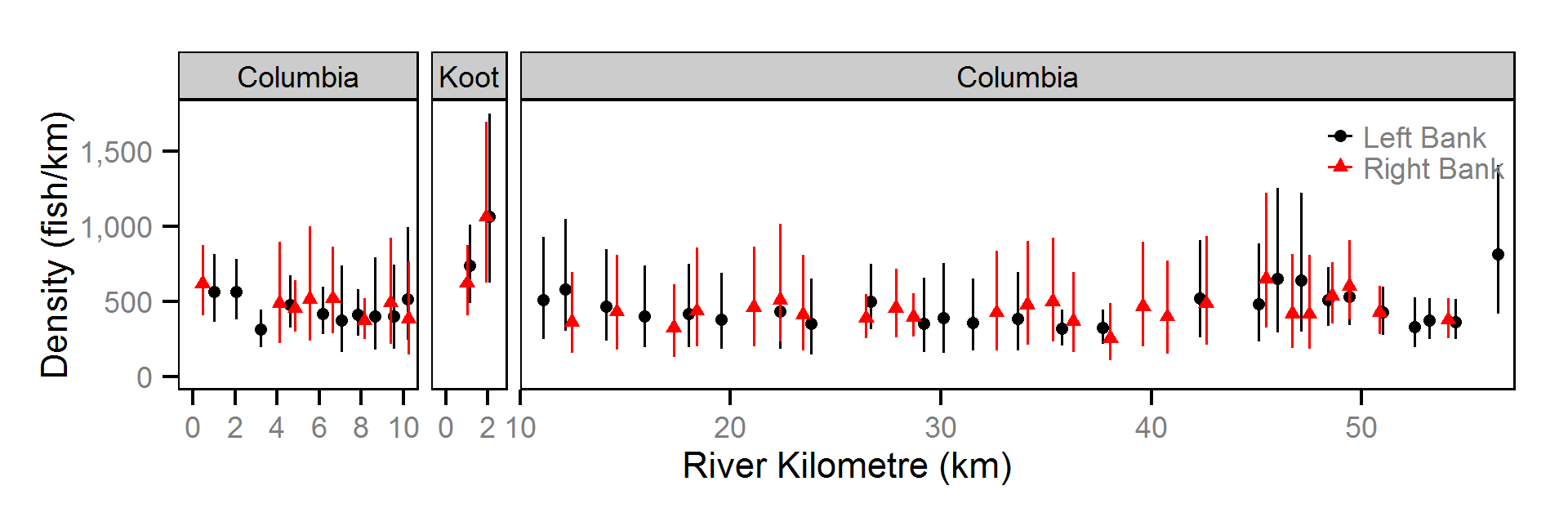
Abundance
The abundance was estimated from the catch and bias-corrected observer count data using an overdispersed Poisson model (Kéry and Schaub (2011)55-56). The model assumed that the capture efficiency was the mean estimate from the capture efficiency model and that the number of observed fish was a multiple of the number of captured fish. The annual abundance estimates represent the total number of fish in the study area.
Key assumptions of the abundance model include:
- The capture efficiency is the mean estimate from the capture efficiency model.
- The observer efficiency varies from the capture efficiency.
- The lineal fish density varies randomly with site, year and site within year.
- The catches and counts are described by a Poisson-gamma distribution.
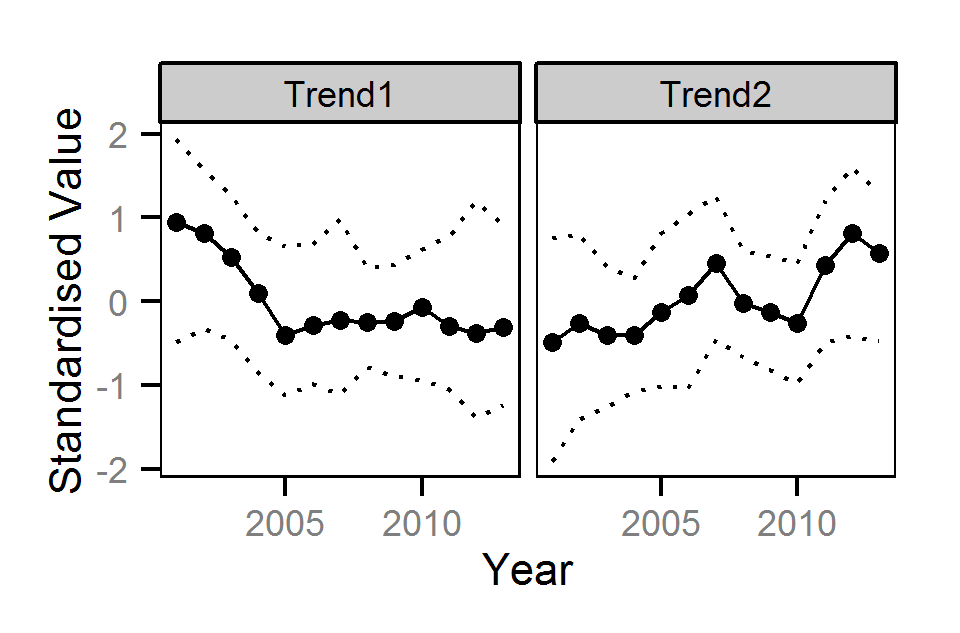
Dynamic Factor Analysis
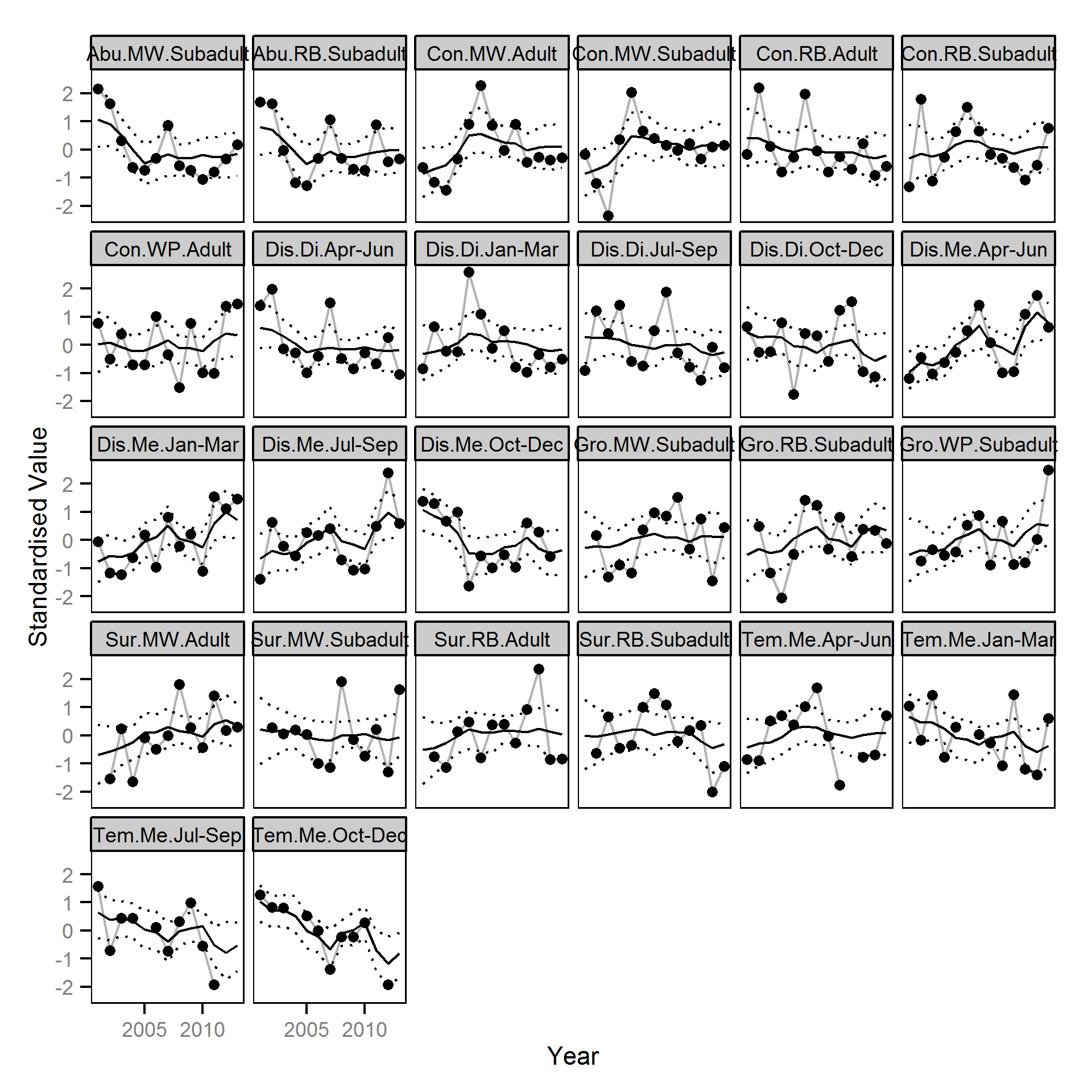
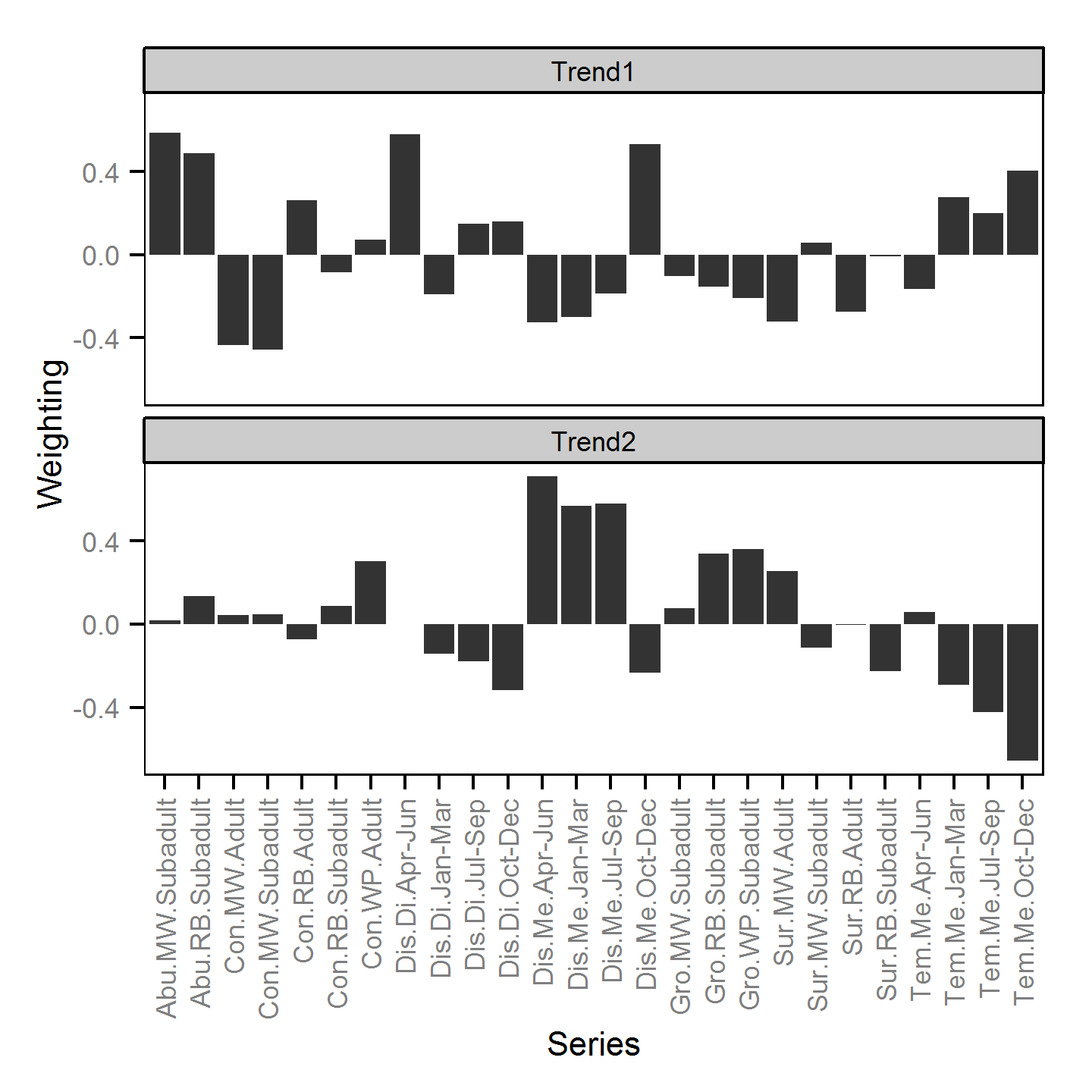
Trends common to the fish index and environmental annual time series were identified using Dynamic Factor Analysis (Zuur et al. (2003)) - a dimension-reduction technique especially designed for time-series data.
The fish index time series were the growth (Gro..), condition (Con..), survival (Sur..) and abundance (Abu..) by species code and life stage. The annual abundance of adults were excluded as the values are the result of survival and subadult abundance across multiple years.
The environmental time series were the mean discharge (Dis.Me..),
and the average hourly absolute discharge difference (Dis.Di..)
at Birchbank and the
average water temperature (Tem.Me..) at Norns Creek by quaterly period. The average hourly absolute discharge difference was calculated by differencing
the mean hourly discharge time series and taking the average of the absolute differences. Mathematically this is equivalent to
\[
\frac{\sum |x_{1}-x_{2}| + |x_{2}-x_{3}| + ... + |x_{n-1}-x_{n}|}{n-1}
\]
where \(x_{1}\) is the discharge at the start of the time series and \(x_{2}\)
is the discharge an hour later.
The ..Oct-Dec times series were lead (opposite of lagged) by one year as they were not expected to influence the fish time series in the same year.
All time series were standardized prior to fitting the DFA model. Key assumptions of the dynamic factor analysis model include:
- The trends are described by independent random walks with
a shared standard deviation.
- The expected value is the sum of the time series weighted trends.
- The SD of the residual variation varies by time series.
- The residual variation is normally distributed.
Preliminary analyses indicated that two trends provided a reasonable model fit
without apparent over-fitting.
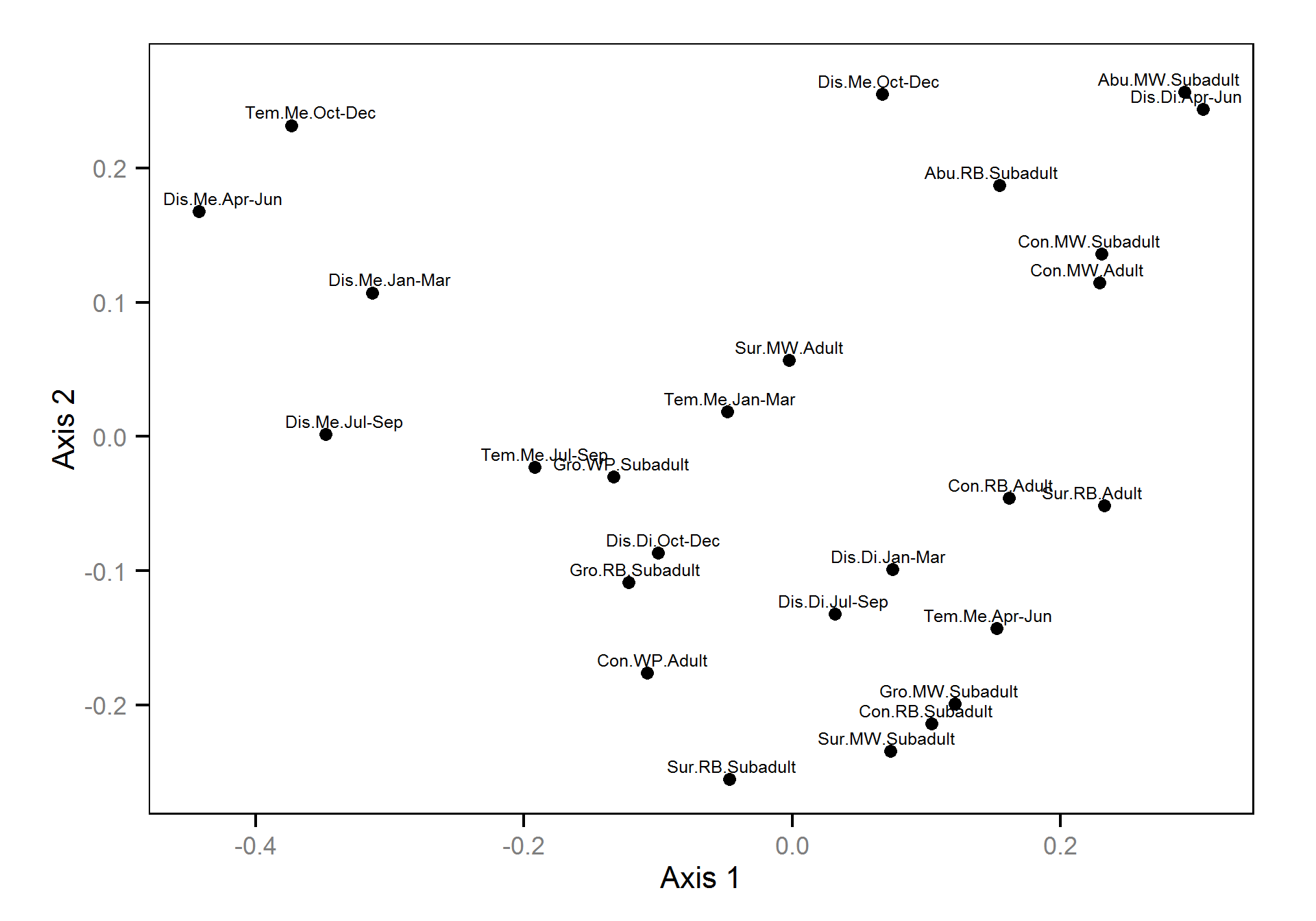
Non-metric multidimensional scaling was used to indicate the clustering of time series based on the absolute DFA trend weightings
Model Code
The JAGS model code, which uses a series of naming conventions, is presented below.
Condition
bCorrelation |
Correlation coefficient between sWeightYear and sWeightLengthYear |
bWeight |
Intercept for eLogWeight |
bWeightDayte |
Effect of Dayte on eLogWeight |
bWeightLength |
Effect of Length on eLogWeight |
bWeightLengthDayte |
Effect of Dayte on effect of Length on eLogWeight |
bWeightLengthYear |
Effect of Year on effect of Length on eLogWeight |
bWeightYear |
Effect of Year on eLogWeight |
Dayte[i] |
Day of year ith fish was captured |
eLogWeight[i] |
Expected log(weight) of ith fish |
Length[i] |
Log length of ith fish |
sWeight |
SD of residual variation in log(Weight) |
sWeightLengthYear |
SD of effect of Year on effect of Length on eLogWeight |
sWeightYear |
SD of effect of Year on eLogWeight |
Weight[i] |
Observed weight of ith fish |
Year[i] |
Year ith fish was captured |
Condition - Model1
model {
bWeight ~ dnorm(5, 5^-2)
bWeightLength ~ dnorm(3, 5^-2)
bWeightDayte ~ dnorm(0, 5^-2)
bWeightLengthDayte ~ dnorm(0, 5^-2)
eMu[1] <- bWeight
eMu[2] <- bWeightLength
dR[1,1] <- 0.1
dR[1,2] <- 0
dR[2,1] <- 0
dR[2,2] <- 0.1
eOmega ~ dwish(dR, 2)
for (i in 1:nYear) {
eYear[i, 1:2] ~ dmnorm(eMu, eOmega)
bWeightYear[i] <- eYear[i, 1] - bWeight
bWeightLengthYear[i] <- eYear[i, 2] - bWeightLength
}
eS2 <-inverse(eOmega)
sWeightYear <- sqrt(eS2[1,1])
sWeightLengthYear <- sqrt(eS2[2,2])
bCorrelation <- eS2[1,2] / sqrt(eS2[1,1] * eS2[2,2])
sWeight ~ dunif(0, 5)
for(i in 1:length(Length)) {
eLogWeight[i] <- bWeight + bWeightDayte * Dayte[i] + bWeightYear[Year[i]] + (bWeightLength + bWeightLengthDayte * Dayte[i] + bWeightLengthYear[Year[i]]) * Length[i]
Weight[i] ~ dlnorm(eLogWeight[i], sWeight^-2)
}
}
Growth
bK |
Intercept for log(eK) |
bKYear[i] |
Effect of ith year on log(eK) |
bLinf |
Mean maximum length |
eGrowth[i] |
Expected growth between release and recapture of ith recapture |
eK[i] |
Expected von Bertalanffy growth coefficient in ith year |
Growth[i] |
Observed growth between release and recapture of ith recapture |
LengthAtRelease[i] |
Previous length at release of ith recapture |
sGrowth |
SD of residual variation in Growth |
sKYear |
SD of effect of ith year on log(eK) |
Year[i] |
Release year of ith recapture |
Years[i] |
Years between release and recapture of ith recapture |
Growth - Model1
model {
bK ~ dnorm (0, 5^-2)
sKYear ~ dunif (0, 5)
for (i in 1:nYear) {
bKYear[i] ~ dnorm(0, sKYear^-2)
log(eK[i]) <- bK + bKYear[i]
}
bLinf ~ dunif(100, 1000)
sGrowth ~ dunif(0, 100)
for (i in 1:length(Year)) {
eGrowth[i] <- (bLinf - LengthAtRelease[i]) * (1 - exp(-sum(eK[Year[i]:(Year[i] + Years[i] - 1)])))
Growth[i] ~ dnorm(eGrowth[i], sGrowth^-2)
}
}
Length-At-Age
Age[i] |
Age of ith fish observed |
bAgeYear |
Effect of Age within Year on eLength |
bDayte[j] |
Linear effect of Dayte on eLength for a jth aged fish |
bDayte2[j] |
Quadratic effect of Dayte on eLength for a jth aged fish |
bIntercept[j] |
Intercept of eLength for a jth aged fish |
Dayte[i] |
Day of year ith fish was observed |
eIncrement[i] |
Length difference between an ith aged fish and an (i-1)th aged fish |
eLength[i] |
Expected length of ith fish |
Length[i] |
Observed length of ith fish |
pAge[i] |
Proportion of fish belonging to jth age |
sAgeYear |
SD of effect of Age within Year on eLength |
sLengthAge[j] |
SD of residual variation in eLength for a jth aged fish |
Year[i] |
Year ith fish was observed |
Length-At-Age - Model1
model {
for(i in 1:nAge) {
dAge[i] <- 1
eIncrement[i] ~ dunif(50, 250)
bDayte[i] ~ dnorm(0, 10)
bDayte2[i] ~ dnorm(0, 10)
sAgeYear[i] ~ dunif(0, 50)
for(j in 1:nYear) {
bAgeYear[i, j] ~ dnorm(0, sAgeYear[i]^-2) }
sLengthAge[i] ~ dunif(0, 100)
}
bIntercept[1] <- eIncrement[1]
for(i in 2:nAge) {
bIntercept[i] <- bIntercept[i-1] + eIncrement[i]
}
pAge[1:nAge] ~ ddirch(dAge[])
for (i in 1:length(Length)) {
Age[i] ~ dcat(pAge[])
eLength[i] <- bIntercept[Age[i]] + bDayte[Age[i]] * Dayte[i] + bDayte2[Age[i]] * Dayte[i]^2 + bAgeYear[Age[i],Year[i]]
Length[i] ~ dnorm(eLength[i], sLengthAge[Age[i]]^-2)
}
}
Length Bias
bLength |
Effect of Observer on eLength |
ClassWidth |
Width of classes |
eLength[i] |
Expected actual length class of ith fish |
Length[i] |
Observed length of ith fish |
Observer[i] |
Observer of ith fish |
sLength |
SD of residual variation in length class |
Length Bias - Model1
model {
for(i in 1:Classes) {
dLengthClass[i] <- 1
}
pLengthClass[1:Classes] ~ ddirch(dLengthClass[])
bLength[1] <- 1
sLength[1] <- 0.01
for(i in 2:nObserver) {
bLength[i] ~ dunif(0.5, 2)
sLength[i] ~ dunif(0.5, 2)
}
for(i in 1:length(Length)) {
eLengthClass[i] ~ dcat(pLengthClass[])
eLength[i] <- bLength[Observer[i]] * eLengthClass[i]
Length[i] ~ dnorm(eLength[i] * ClassWidth, (sLength[Observer[i]] * ClassWidth)^-2)
}
}
Survival
bEfficiency |
Intercept for logit(eEfficiency) |
bSurvivalInterceptStage |
Intercept for logit(eSurvival) by Stage |
bSurvivalStageYear |
Effect of Year on logit(eSurvival) by Stage |
eAlive[i, j] |
Expected state (alive or dead) of ith fish in jth year |
eEfficiency[i, j] |
Expected recapture probability of ith fish in jth year |
eSurvival[i, j] |
Expected survival probability of ith fish in jth year |
FirstYear[i] |
First year ith fish was observed |
FishYear[i, j] |
Whether ith fish was observed in jth year |
sSurvivalStageYear |
SD of effect of Year on logit(eSurvival) by Stage |
StageFishYear[i, j] |
Stage of ith fish in jth year |
Survival - Model1
model {
bEfficiency ~ dnorm (0, 5^-2)
for (i in 1:nStage) {
sSurvivalStageYear[i] ~ dunif (0, 5)
}
for(i in 1:nStage) {
bSurvivalInterceptStage[i] ~ dnorm(0, 5^-2)
for (j in 1:nYear) {
bSurvivalStageYear[i,j] ~ dnorm (0, sSurvivalStageYear[i]^-2)
}
}
for (i in 1:nFish) {
eAlive[i, FirstYear[i]] <- 1
for (j in (FirstYear[i]+1):nYear) {
logit(eEfficiency[i,j]) <- bEfficiency
logit(eSurvival[i,j-1]) <- bSurvivalInterceptStage[StageFishYear[i,j-1]] + bSurvivalStageYear[StageFishYear[i,j-1],j-1]
eAlive[i,j] ~ dbern (eAlive[i,j-1] * eSurvival[i,j-1])
FishYear[i,j] ~ dbern (eAlive[i,j] * eEfficiency[i,j])
}
}
}
Site Fidelity
bFidelity |
Intercept for logit(eFidelity) |
bLength |
Effect of Length on logit(eFidelity) |
eFidelity[i] |
Expected site fidelity for ith recapture |
Fidelity[i] |
Whether or not ith recapture was encounterd at the same site as the previous encounter |
Length[i] |
Length of ith recapture at previous encounter |
Site Fidelity - Model1
model {
bFidelity ~ dnorm(0, 2^-2)
bLength ~ dnorm(0, 2^-2)
for (i in 1:length(Fidelity)) {
logit(eFidelity[i]) <- bFidelity + bLength * Length[i]
Fidelity[i] ~ dbern(eFidelity[i])
}
}
Capture Efficiency
bEfficiency |
Intercept for logit(eEfficiency) |
bEfficiencySessionYear |
Effect of Session within Year on logit(eEfficiency) |
eEfficiency[i] |
Expected efficiency on ith visit |
eFidelity[i] |
Expected site fidelity on ith visit |
Fidelity[i] |
Mean site fidelity on ith visit |
FidelitySD[i] |
SD of site fidelity on ith visit |
Recaptures[i] |
Number of marked fish recaught during ith visit |
sEfficiencySessionYear |
SD of effect of Session within Year on logit(eEfficiency) |
Session[i] |
Session of ith visit |
Tagged[i] |
Number of marked fish tagged prior to ith visit |
Year[i] |
Year of ith visit |
Capture Efficiency - Model1
model {
bEfficiency ~ dnorm(0, 5^-2)
sEfficiencySessionYear ~ dunif(0, 2)
for (i in 1:nSession) {
for (j in 1:nYear) {
bEfficiencySessionYear[i, j] ~ dnorm(0, sEfficiencySessionYear^-2)
}
}
for(i in 1:length(Year)) {
logit(eEfficiency[i]) <- bEfficiency + bEfficiencySessionYear[Session[i], Year[i]]
eFidelity[i] ~ dnorm(Fidelity[1], FidelitySD[1]^-2) T(0, 1)
Recaptures[i] ~ dbin(eEfficiency[i] * eFidelity[i], Tagged[i])
}
}
Abundance
bDensity |
Intercept for log(eDensity) |
bDensitySite |
Effect of Site on log(eDensity) |
bDensitySiteYear |
Effect of Site within Year on log(eDensity) |
bDensityYear |
Effect of Year on log(eDensity) |
bType |
Effect of Type on Efficiency |
Count[i] |
Observed count during ith visit |
eDensity[i] |
Expected density during ith visit |
eDispersion |
Overdispersion of Count |
Efficiency[i] |
Survey efficiency during ith visit |
ProportionSampled[i] |
Proportion of site surveyed during ith visit |
sDensitySite |
SD of effect of Site on log(eDensity) |
sDensitySiteYear |
SD of effect of Site within Year on log(eDensity) |
sDensityYear |
SD of effect of Year on log(eDensity) |
sDispersion |
SD of overdispersion term |
Site[i] |
Site of ith visit |
SiteLength[i] |
Length of site during ith visit |
Type[i] |
Survey type (catch versus count) during ith visit |
Year[i] |
Year of ith visit |
Abundance - Model1
model {
bDensity ~ dnorm(5, 5^-2)
bType[1] <- 1
for (i in 2:nType) {
bType[i] ~ dunif(0, 10)
}
sDensityYear ~ dunif(0, 2)
for (i in 1:nYear) {
bDensityYear[i] ~ dnorm(0, sDensityYear^-2)
}
sDensitySite ~ dunif(0, 2)
sDensitySiteYear ~ dunif(0, 2)
for (i in 1:nSite) {
bDensitySite[i] ~ dnorm(0, sDensitySite^-2)
for (j in 1:nYear) {
bDensitySiteYear[i, j] ~ dnorm(0, sDensitySiteYear^-2)
}
}
sDispersion ~ dunif(0, 5)
for (i in 1:length(Count)) {
log(eDensity[i]) <- bDensity + bDensitySite[Site[i]] + bDensityYear[Year[i]] + bDensitySiteYear[Site[i],Year[i]]
eDispersion[i] ~ dgamma(1 / sDispersion^2, 1 / sDispersion^2)
Count[i] ~ dpois(eDensity[i] * SiteLength[i] * ProportionSampled[i] * Efficiency[i] * bType[Type[i]] * eDispersion[i])
}
}
Dynamic Factor Analysis
bTrend[i,j] |
Value of ith trend in jth Year |
bWeighting[i,j] |
Weighting of ith Trend for jth Series |
Series[i] |
Time series of ith value |
sSeries[i] |
SD for ith Series |
sTrend |
SD for bTrend |
Value[i] |
ith value |
Year[i] |
Year of ith value |
Dynamic Factor Analysis - Model1
model {
sTrend ~ dunif(0, 1)
for(i in 1:nTrend) {
muTrend[i] <- 0
for(j in 1:nTrend) {
oTrend[i,j] <- ifelse(i == j, sTrend^-2, 0)
}
for(j in 1:nSeries) {
eWeighting[i,j] ~ dunif(-1, 1)
aWeighting[i,j] <- eWeighting[i,j] * ifelse(j < nTrend andand i > j, 0, 1)
bWeighting[i,j] <- ifelse(j <= nTrend andand i == j, abs(aWeighting[i,j]), aWeighting[i,j])
}
}
bTrend[1:nTrend, 1] ~ dmnorm(muTrend, oTrend / 25)
for(j in 2:nYear) {
bTrend[1:nTrend, j] ~ dmnorm(bTrend[1:nTrend,j-1], oTrend)
}
for(i in 1:nSeries) {
sSeries[i] ~ dunif(0, 1)
}
for(i in 1:length(Value)) {
eValue[i] <- sum(bWeighting[,Series[i]] * bTrend[,Year[i]])
Value[i] ~ dnorm(eValue[i], sSeries[Series[i]]^-2)
}
}