Duncan Lardeau Juvenile Rainbow Trout Abundance 2018
The suggested citation for this analytic report is:
Thorley, J.L., Andrusak, G.F., and Dalgarno, S. (2018) Duncan Lardeau Juvenile Rainbow Trout Abundance 2018. A Poisson Consulting Analysis Report. URL: https://www.poissonconsulting.ca/f/679886444.
Background
Rainbow Trout rear in the Lardeau and Lower Duncan rivers. Since 2006 (with the exception of 2015) annual spring snorkel surveys have been conducted to estimate the abundance and distribution of age-1 Rainbow Trout. From 2006 to 2010 the surveys were conducted at fixed index sites. Since 2011 fish observations have been mapped to the river based on their spatial coordinates as recorded by GPS.
The primary aims of the current analyses were to:
- Estimate the spring abundance of age-1 fish by year.
- Estimate the egg deposition.
- Estimate the stock-recruitment relationship between the egg deposition and the abundance of age-1 recruits the following spring.
- Estimate a Limit Reference Point (LRP) for the egg deposition (and number of spawners).
- Estimate the maximum reproductive rate (spawners per spawner at low density).
- Rerun preliminary yield-per-recruit estimates based on the latest results.
Methods
Data Preparation
The data were provided by the Ministry of Forests, Lands and Natural Resource Operations (MFLNRO). The historical and current snorkel count data were manipulated using R version 3.5.1 (R Core Team 2017) and organised in an SQLite database.
Data Analysis
Hierarchical Bayesian models were fitted to the data using R version
3.5.1 (R Core Team 2017), Stan 2.16.0 (Carpenter et al. 2017) and
JAGS 4.2.0 (Plummer 2015) and the
mbr family of packages.
Unless indicated otherwise, the models used prior distributions that were vague in the sense that they did not affect the posterior distributions (Kery and Schaub 2011, 36). The posterior distributions were estimated from 2,000 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of three chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that \(\hat{R} < 1.1\) (Kery and Schaub 2011, 40) for each of the monitored parameters in the model (Kery and Schaub 2011, 61). Where relevant, model adequacy was confirmed by examination of residual plots.
The posterior distributions of the fixed (Kery and Schaub 2011, 75) parameters are summarised in terms of the point estimate, standard deviation (sd), the z-score, lower and upper 95% confidence/credible limits (CLs) and the p-value (Kery and Schaub 2011, 37, 42). The estimate is the median (50th percentile) of the MCMC samples, the z-score is \(\mathrm{mean}/\mathrm{sd}\) and the 95% CLs are the 2.5th and 97.5th percentiles. A p-value of 0.05 indicates that the lower or upper 95% CL is 0.
Variable selection was achieved by dropping fixed (Kery and Schaub 2011, 77–82) variables with two-sided p-values \(\geq\) 0.05 (Kery and Schaub 2011, 37, 42) and random variables with percent relative errors \(\geq\) 80%.
The results are displayed graphically by plotting the modeled relationships between particular variables and the response with 80% or 95% credible intervals (CIs) with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values respectively while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). Where informative the influence of particular variables is expressed in terms of the effect size (i.e., percent change in the response variable) with 95% CIs (Bradford et al. 2005).
Model Descriptions
Length Correction
The annual bias (inaccuracy) and error (imprecision) in observer’s fish length estimates when spotlighting (standing) and snorkeling were quantified from the divergence of their length distribution from the length distribution for all observers (including measured fish) in that year. More specifically, the length correction that minimised the Jensen-Shannon divergence (Lin 1991) between the two distributions provided a measure of the inaccuracy while the minimum divergence (the Jensen-Shannon divergence was calculated with log to base 2 which means it lies between 0 and 1) provided a measure of the imprecision.
After correcting the fish lengths, age-1 individuals were assumed to be those with a fork length \(\leq\) 100 mm.
Abundance
The abundance was estimated from the count data using an overdispersed Poisson model (Kery and Schaub 2011, 55–56). The annual abundance estimates represent the total number of fish in the study area.
Key assumptions of the abundance model include:
- The lineal fish density varies with year, useable width and river kilometer as a polynomial, and randomly with site.
- The observer efficiency at marking sites varies by study design (GPS versus Index).
- The observer efficiency also varies by visit type (marking versus count) within study design and randomly by snorkeller.
- The expected count at a site is the expected lineal density multiplied by the site length, the observer efficiency and the proportion of the site surveyed.
- The residual variation in the actual count is gamma-Poisson distributed.
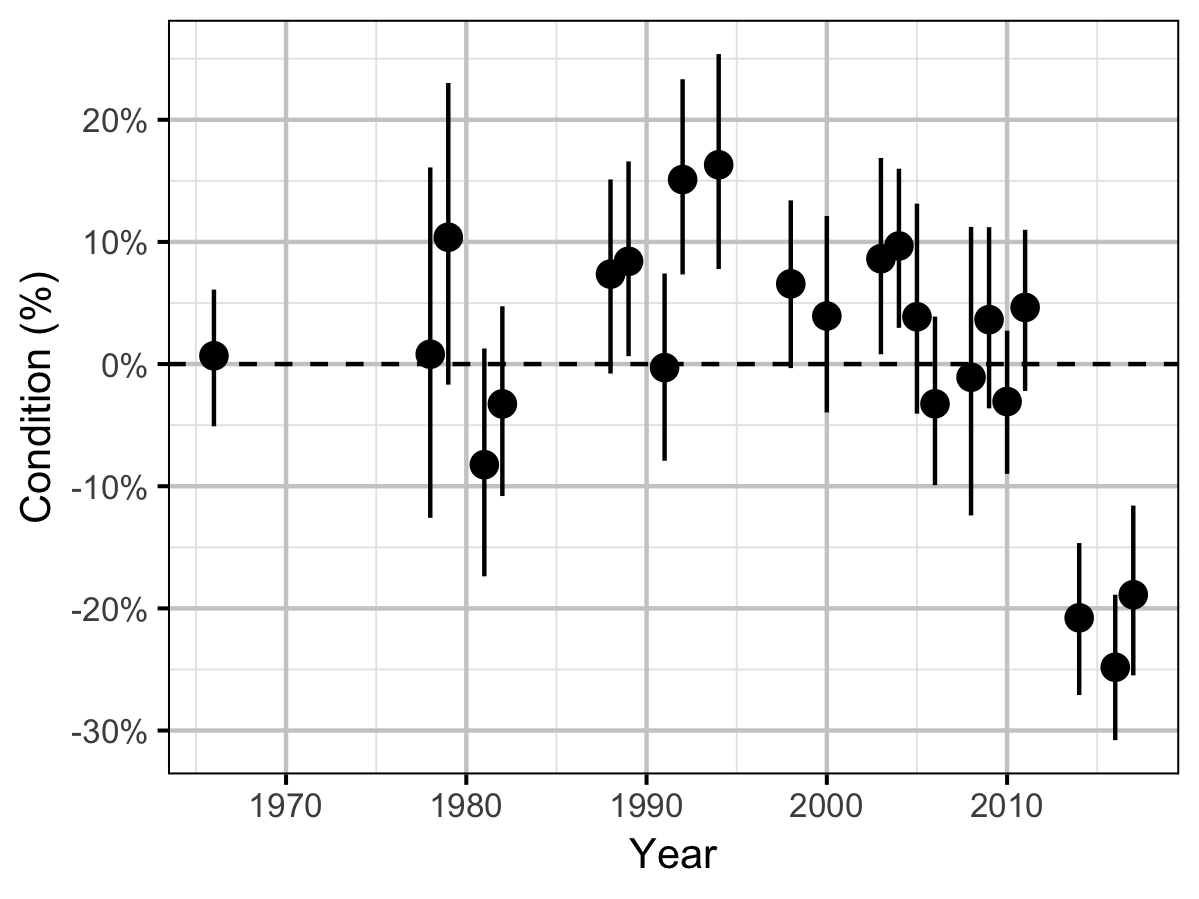
Condition
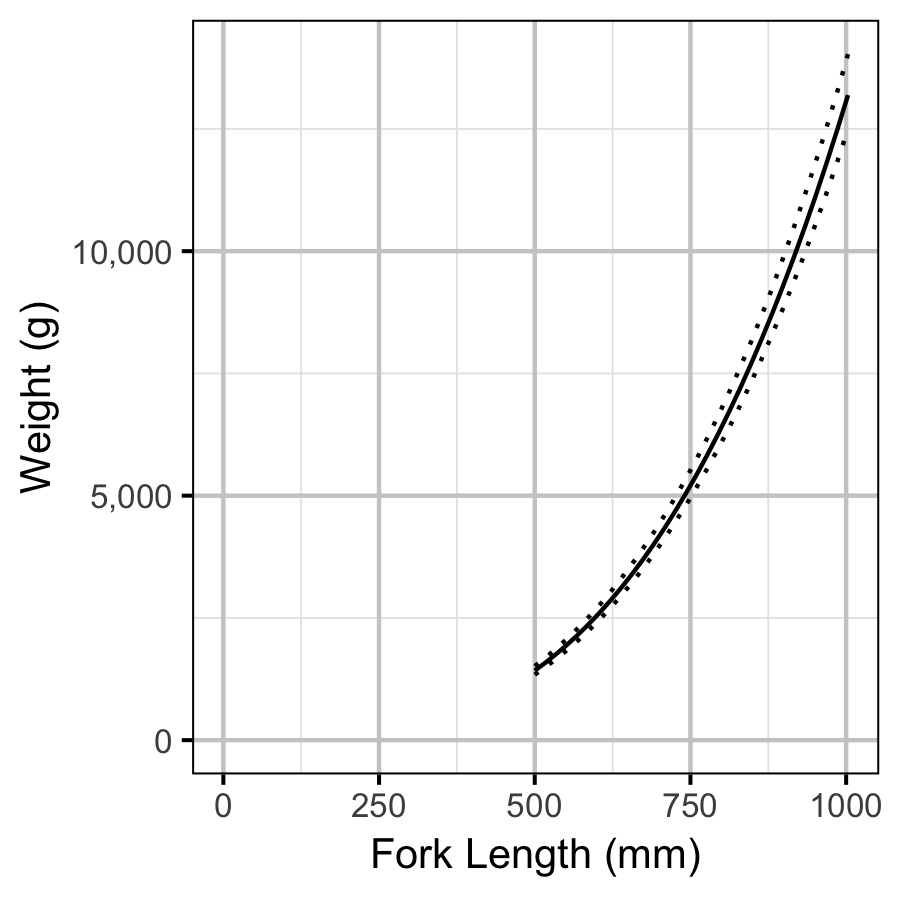
The condition of fish with a fork length \(\geq\) 500 mm was estimated via an analysis of mass-length relations (He et al. 2008).
More specifically the model was based on the allometric relationship
\[ W = \alpha_c L^{\beta_c}\]
where \(W\) is the weight (mass), \(\alpha_c\) is the coefficent, \(\beta_c\) is the exponent and \(L\) is the length.
To improve chain mixing the relation was log-transformed, i.e.,
\[ \log(W) = \log(\alpha_c) + \beta_c \log(L).\]
Key assumptions of the condition model include:
- \(\alpha_c\) can vary randomly by year.
- The residual variation in weight is log-normally distributed.
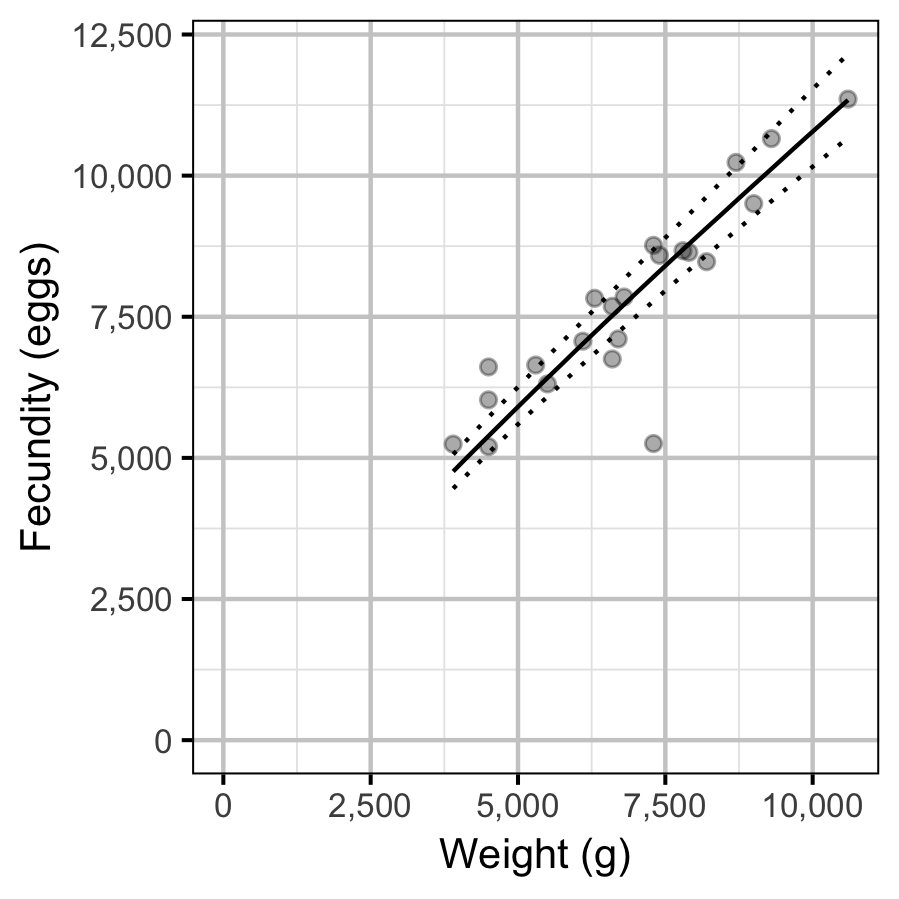
Fecundity
The fecundity of females with a fork length \(\geq\) 500 mm was estimated via an analysis of fecundity-mass relations.
More specifically the model was based on the allometric relationship
\[ F = \alpha_f W^{\beta_f}\]
where \(F\) is the fecundity, \(\alpha_f\) is the coefficent, \(\beta_f\) is the exponent and \(W\) is the weight.
To improve chain mixing the relation was log-transformed.
Key assumptions of the fecundity model include:
- The residual variation in fecundity is log-normally distributed.
Spawner Size
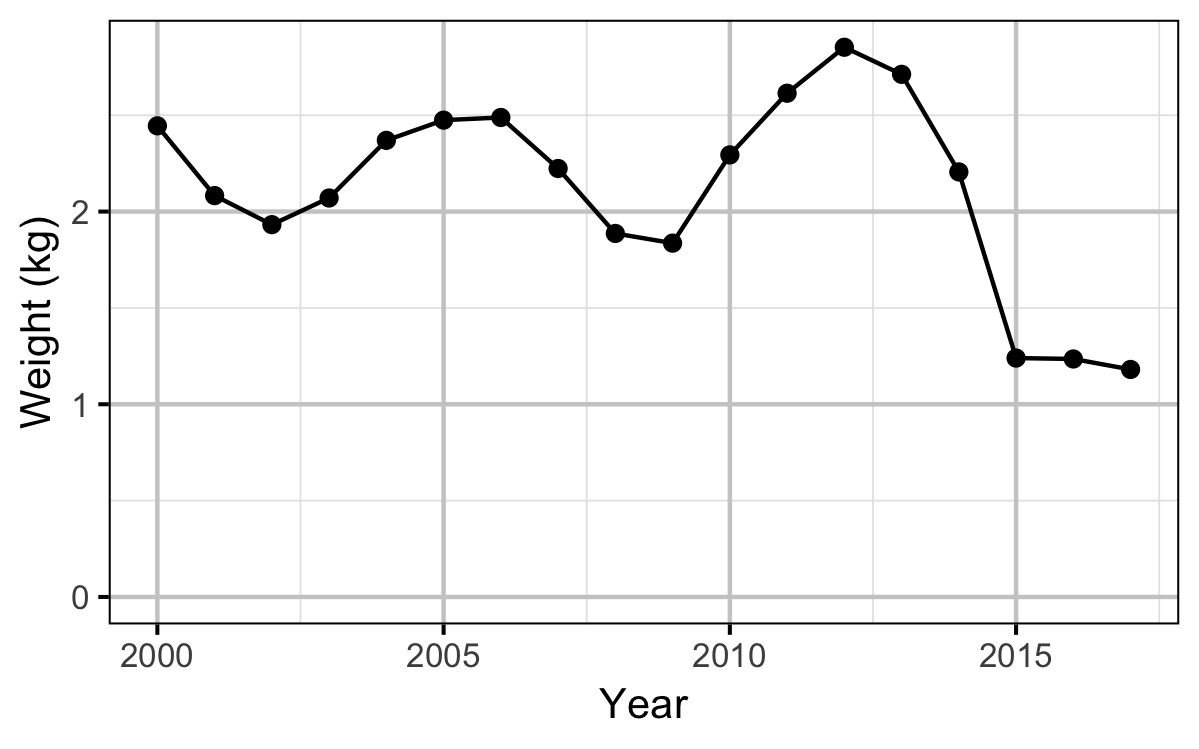
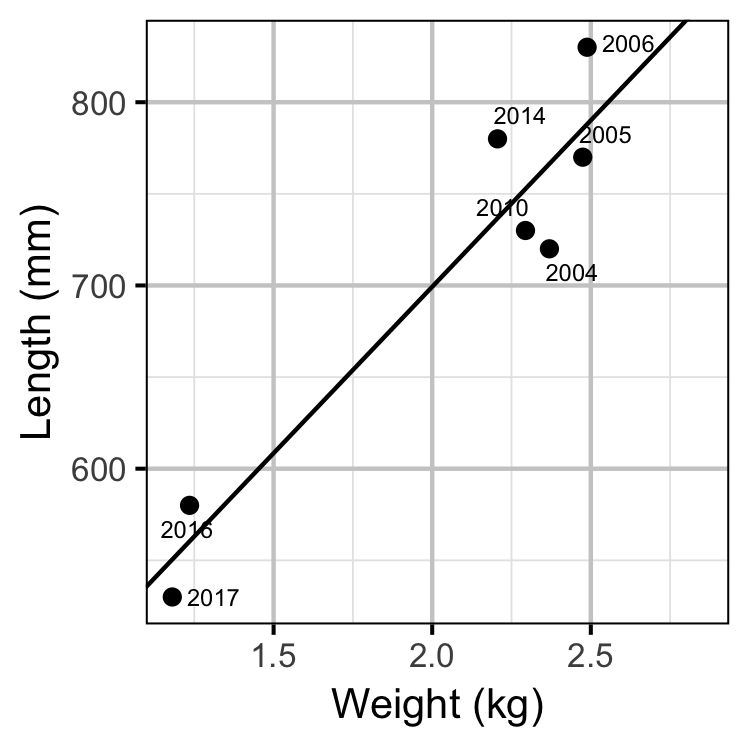
The average length of the spawners in each year (for years for which it was unavailable) was estimated from the mean weight of Rainbow Trout in the Kootenay Lake Rainbow Trout Mailout Survey (KLRT) using a linear regression. This approach was suggested by Rob Bison.
Egg Deposition
The egg deposition in each year was estimated by
- converting the average length of spawners to the average weight using the condition relationship for a typical year
- adjusting the average weight by the annual condition effect (interpolating where unavailable)
- converting the average weight to the average fecundity using the fecundity relationship
- multiplying the average fecundity by the AUC based estimate of the number of females (assuming a sex ratio of 1:1)
Stock-Recruitment
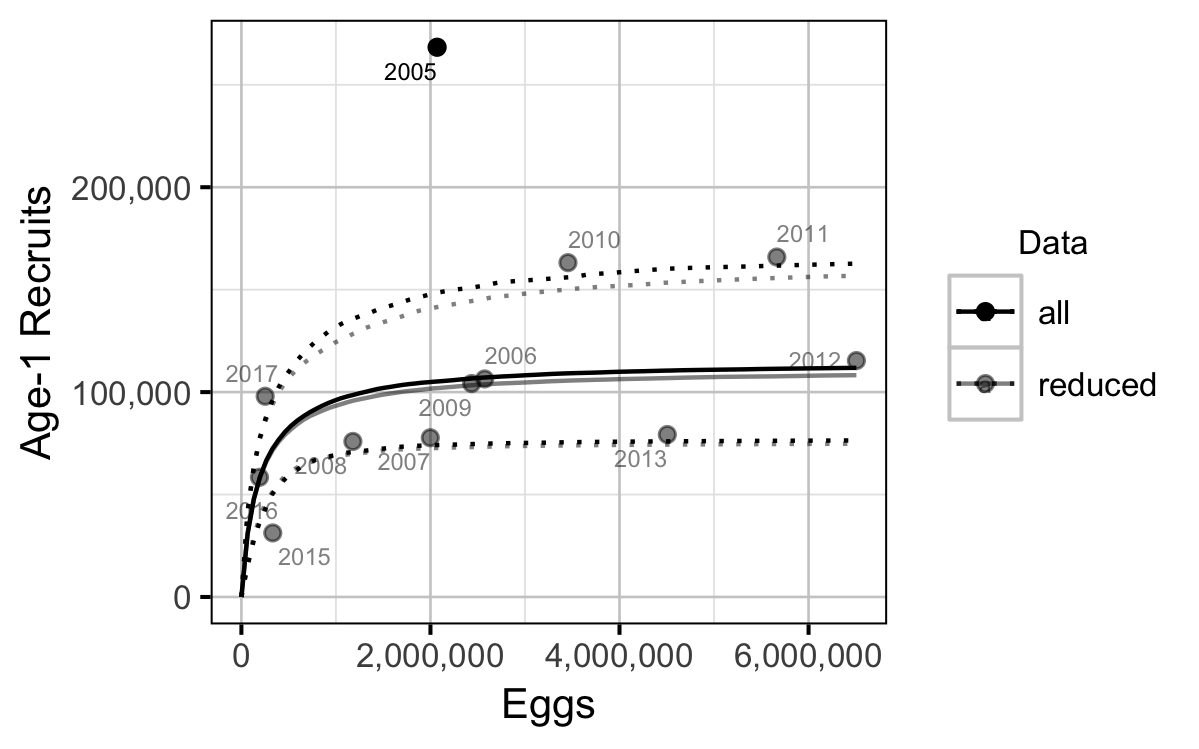
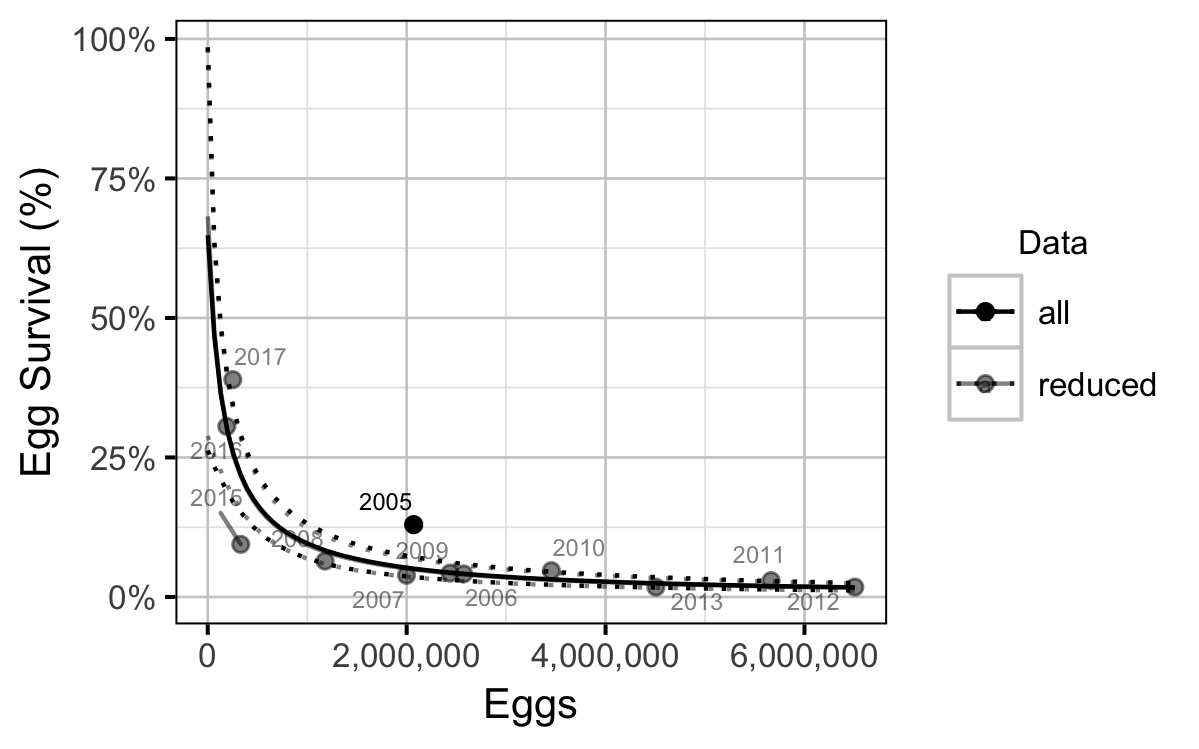
The relationship between the number of eggs (\(E\)) and the abundance of age-1 individuals the following spring (\(R\)) was estimated using a Beverton-Holt stock-recruitment model (Walters and Martell 2004):
\[ R = \frac{\alpha_s \cdot E}{1 + \beta_s \cdot E} \quad,\]
where \(\alpha_s\) is the maximum number of recruits per egg (egg survival), and \(\beta_s\) is the density dependence.
Key assumptions of the stock-recruitment model include:
- The residual variation in the number of recruits is log-normally distributed with the standard deviation scaling with the uncertainty in the number of recruits.
The age-1 carrying capacity (\(K\)) is given by:
\[ K = \frac{\alpha_s}{\beta_s} \quad.\]
and the \(E_{K/2}\) Limit Reference Point (Mace 1994, \(E_{0.5 R_{max}}\)), which corresponds to the stock (number of eggs) that produce 50% of the maximum recruitment (\(K\)), by \[E_{K/2} = \frac{1}{\beta_s}\]
The LRP was also converted into a number of spawners in a typical year (assuming 6,000 eggs per spawner and a sex ratio of 1:1).
Environmental
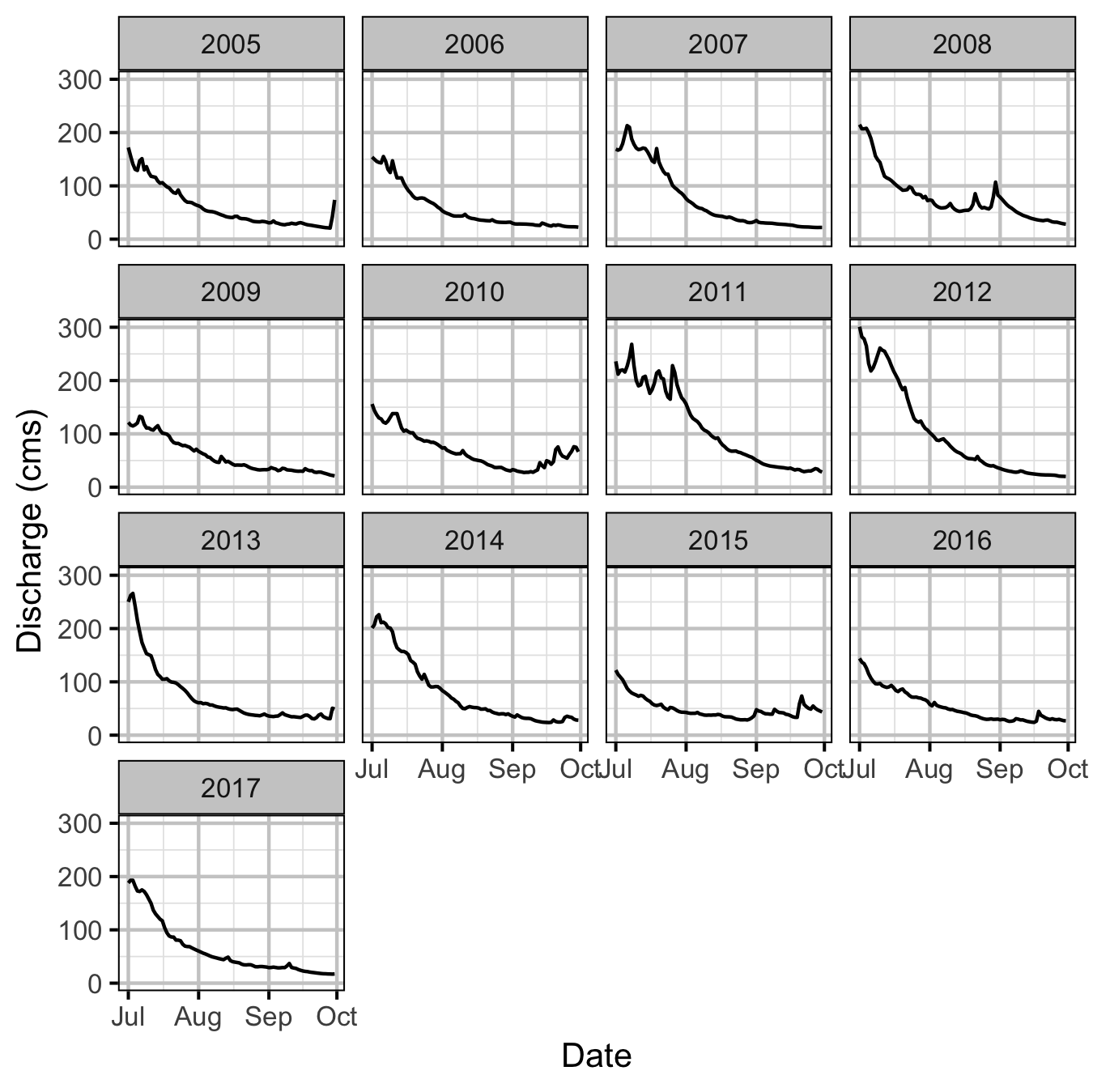
The mean daily discharge in the Lardeau at the Water Survey of Canada Marblehead site (08NH007) was plotted during the emergence period to see if an unusual hydrograph may have been responsible for the high recruitment from the 2005 spawn year.
Reproductive Rate
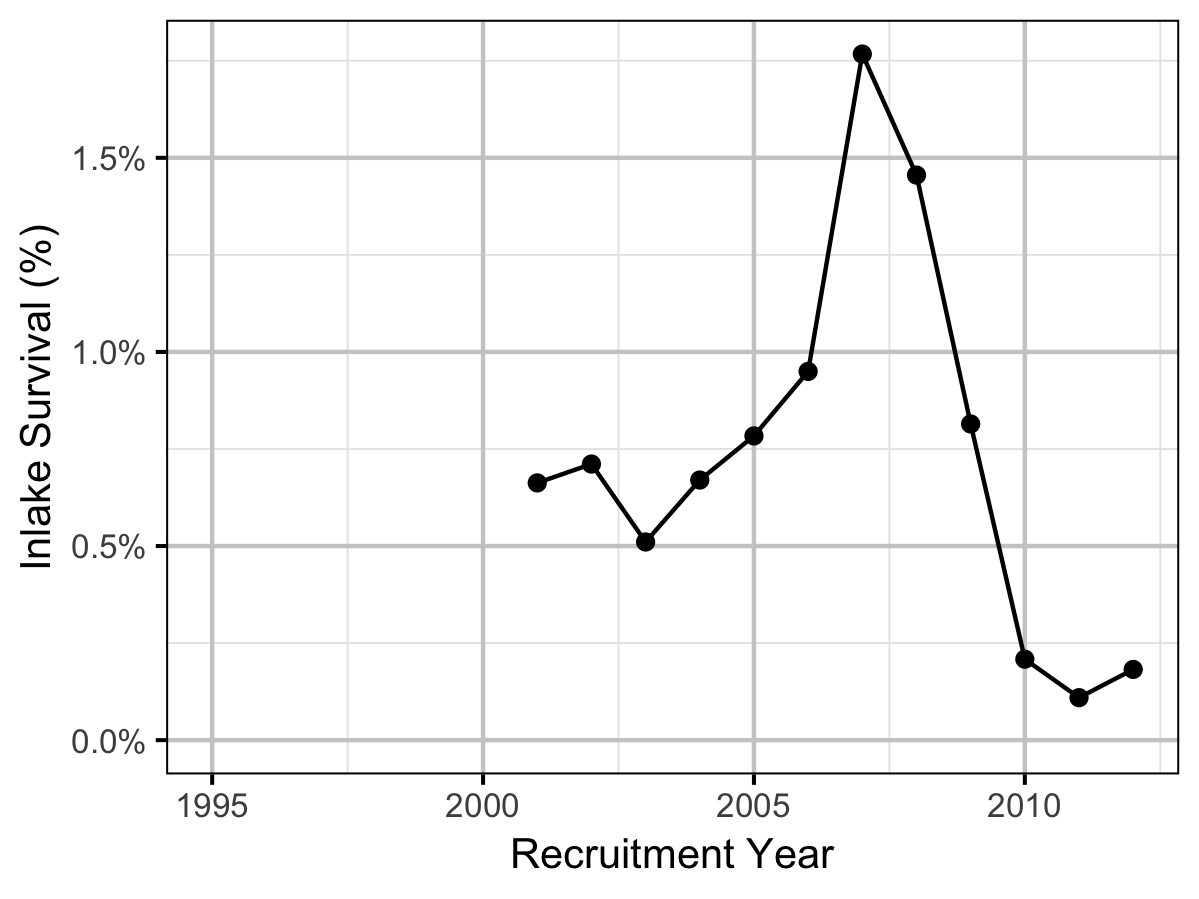
The maximum reproductive rate (the number of spawners per spawner at low density) not accounting for fishing mortality was calculated by multiplying \(\beta_s\) (number of recruits per egg at low density) from the stock-recruitment relationship by the inlake survival by the average number of eggs per spawner in a typical year (assumed to be 3,000 based on 6,000 eggs per spawner and a sex ratio of 1:1). The inlake survival from age-1 to spawning was calculated by dividing the subsequent number of spawners by the number of recruits assuming that equal numbers of fish spawn at age 5, 6 and 7.
Yield-per-Recruit
The optimal capture rate and egg deposition was estimated using the ypr R package.
Model Templates
Abundance
data {
int<lower=0> nMarked;
int<lower=0> Marked[nMarked];
int<lower=0> Resighted[nMarked];
int<lower=0> IndexMarked[nMarked];
int<lower=0> nObs;
int Marking[nObs];
int Index[nObs];
int<lower=0> nSwimmer;
int<lower=0> Swimmer[nObs];
int<lower=0> nYear;
int<lower=0> Year[nObs];
real Width[nObs];
real Rkm[nObs];
int<lower=0> nSite;
int<lower=0> Site[nObs];
real SiteLength[nObs];
real SurveyProportion[nObs];
int Count[nObs];
}
parameters {
real bEfficiency;
real bEfficiencyIndex;
real bDensity;
vector[nYear] bDensityYear;
real bDensityWidth;
vector[4] bDensityRkm;
real<lower=0> sDensitySite;
vector[nSite] bDensitySite;
real bEfficiencyMarking;
real bEfficiencyMarkingIndex;
real<lower=0,upper=5> sEfficiencySwimmer;
vector[nSwimmer] bEfficiencySwimmer;
real<lower=0> sDispersion;
}
model {
vector[nObs] eDensity;
vector[nObs] eEfficiency;
vector[nObs] eAbundance;
vector[nObs] eCount;
sDispersion ~ gamma(0.01, 0.01);
bDensity ~ normal(0, 2);
bDensityRkm ~ normal(0, 2);
sDensitySite ~ uniform(0, 5);
bDensitySite ~ normal(0, sDensitySite);
bDensityWidth ~ normal(0, 2);
bDensityYear ~ normal(0, 5);
bEfficiency ~ normal(0, 5);
bEfficiencyIndex ~ normal(0, 5);
bEfficiencyMarking ~ normal(0, 5);
bEfficiencyMarkingIndex ~ normal(0, 5);
sEfficiencySwimmer ~ uniform(0, 5);
bEfficiencySwimmer ~ normal(0, sEfficiencySwimmer);
for (i in 1:nMarked) {
target += binomial_lpmf(Resighted[i] | Marked[i],
inv_logit(
bEfficiency +
bEfficiencyIndex * IndexMarked[i] +
bEfficiencyMarking +
bEfficiencyMarkingIndex * IndexMarked[i]
));
}
for (i in 1:nObs) {
eDensity[i] = exp(bDensity +
bDensityRkm[1] * Rkm[i] +
bDensityRkm[2] * pow(Rkm[i], 2.0) +
bDensityRkm[3] * pow(Rkm[i], 3.0) +
bDensityRkm[4] * pow(Rkm[i], 4.0) +
bDensitySite[Site[i]] +
bDensityYear[Year[i]] +
bDensityWidth * log(Width[i]));
eEfficiency[i] = inv_logit(
bEfficiency +
bEfficiencyIndex * Index[i] +
bEfficiencyMarking * Marking[i] +
bEfficiencyMarkingIndex * Index[i] * Marking[i] +
bEfficiencySwimmer[Swimmer[i]]);
eAbundance[i] = eDensity[i] * SiteLength[i];
eCount[i] = eAbundance[i] * eEfficiency[i] * SurveyProportion[i];
}
target += neg_binomial_2_lpmf(Count | eCount, sDispersion);
}Template 1. Abundance model description.
Condition
data {
int nYear;
int nObs;
vector[nObs] Length;
vector[nObs] Weight;
int Year[nObs];
parameters {
real bWeight;
real bWeightLength;
real sWeightYear;
vector[nYear] bWeightYear;
real sWeight;
model {
vector[nObs] eWeight;
bWeight ~ normal(-10, 5);
bWeightLength ~ normal(3, 2);
sWeightYear ~ normal(-2, 5);
for (i in 1:nYear) {
bWeightYear[i] ~ normal(0, exp(sWeightYear));
}
sWeight ~ normal(-2, 5);
for(i in 1:nObs) {
eWeight[i] = bWeight + bWeightLength * log(Length[i]) + bWeightYear[Year[i]];
Weight[i] ~ lognormal(eWeight[i], exp(sWeight));
}Template 2.
Fecundity
data {
int nObs;
vector[nObs] Weight;
vector[nObs] Fecundity;
parameters {
real bFecundity;
real bFecundityWeight;
real sFecundity;
model {
vector[nObs] eFecundity;
bFecundity ~ uniform(0, 5);
bFecundityWeight ~ uniform(0, 2);
sFecundity ~ uniform(0, 1);
for(i in 1:nObs) {
eFecundity[i] = log(bFecundity) + bFecundityWeight * log(Weight[i]);
Fecundity[i] ~ lognormal(eFecundity[i], sFecundity);
}Template 3.
Stock-Recruitment
model {
a ~ dunif(0, 1)
b ~ dunif(0, 0.1)
sScaling ~ dunif(0, 5)
eRecruits <- a * Stock / (1 + Stock * b)
for(i in 1:nObs) {
esRecruits[i] <- SDLogRecruits[i] * sScaling
Recruits[i] ~ dlnorm(log(eRecruits[i]), esRecruits[i]^-2)
}Template 4. Stock-Recruitment model description.
Results
Tables
Abundance
Table 1. Parameter descriptions.
| Parameter | Description |
|---|---|
bDensity |
Intercept for log(eDensity) |
bDensityRkm[x] |
xth-order polynomial coefficients of effect of
river kilometer on bDensity |
bDensitySite[i] |
Effect of ith Site on bDensity |
bDensityWidth |
Effect of Width on bDensity |
bDensityYear[i] |
Effect of ith Year on bDensity |
bEfficiency |
Intercept of logit(eEfficiency) |
bEfficiencyIndex |
Effect of Index on bEfficiency |
bEfficiencyMarking |
Effect of Marking on bEfficiency |
bEfficiencyMarkingIndex |
Effect of Marking and Index on bEfficiency |
bEfficiencySwimmer[i] |
Effect of ith Swimmer on bEfficiency |
eAbundance[i] |
Expected abundance of fish at site of ith visit |
eCount[i] |
Expected total number of fish at site of ith
visit |
eDensity[i] |
Expected lineal density of fish at site of ith
visit |
eEfficiency[i] |
Expected observer efficiency on ith visit |
Index |
Whether the ith visit was to an index site |
Marking[i] |
Whether the ith visit was to a site with marked
fish |
Rkm[i] |
River kilometer of ith visit |
sDensitySite |
SD of bDensitySite |
sDispersion |
Overdispersion of Count[i] |
sEfficiencySwimmer |
SD of bEfficiencySwimmer |
Site[i] |
Site of ith visit |
SiteLength[i] |
Length of site of ith visit |
SurveyProportion[i] |
Proportion of site surveyed on ith visit |
Swimmer[i] |
Snorkeler on ith site visit |
Width[i] |
Useable width of site on ith visit |
Year[i] |
Year of ith site visit |
Table 2. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDensity | -0.6963658 | 1.1641306 | -0.5837528 | -2.8674006 | 1.6429677 | 0.5733 |
| bDensityRkm[1] | -0.2042877 | 0.0944545 | -2.1937619 | -0.3948469 | -0.0329674 | 0.0267 |
| bDensityRkm[2] | 0.6567185 | 0.1097909 | 5.9826906 | 0.4389913 | 0.8767718 | 0.0007 |
| bDensityRkm[3] | 0.0391887 | 0.0378328 | 1.0529303 | -0.0309667 | 0.1144436 | 0.2853 |
| bDensityRkm[4] | -0.2992126 | 0.0360876 | -8.2945201 | -0.3710949 | -0.2305983 | 0.0007 |
| bDensityWidth | 0.0883220 | 0.0273180 | 3.2481475 | 0.0361958 | 0.1421477 | 0.0027 |
| bDensityYear[1] | 0.7529302 | 1.2132431 | 0.6149444 | -1.6731131 | 2.9758967 | 0.5253 |
| bDensityYear[2] | -0.1643764 | 1.2059441 | -0.1412118 | -2.6009230 | 2.1341145 | 0.9080 |
| bDensityYear[3] | -0.4624095 | 1.1997102 | -0.4098222 | -2.8896459 | 1.7299649 | 0.6920 |
| bDensityYear[4] | -0.4846544 | 1.2095951 | -0.4331476 | -2.9586656 | 1.7840561 | 0.6813 |
| bDensityYear[5] | -0.1407823 | 1.2185438 | -0.1595103 | -2.6134068 | 2.1441766 | 0.9000 |
| bDensityYear[6] | 0.2360800 | 1.1643191 | 0.2112010 | -2.0994908 | 2.4362783 | 0.8507 |
| bDensityYear[7] | 0.2463119 | 1.1625706 | 0.2259988 | -2.1796061 | 2.3901774 | 0.8320 |
| bDensityYear[8] | -0.0972376 | 1.1653885 | -0.0839833 | -2.4758856 | 2.0959280 | 0.9387 |
| bDensityYear[9] | -0.4997545 | 1.1614718 | -0.4126908 | -2.8641777 | 1.6887987 | 0.7080 |
| bDensityYear[10] | -1.4189572 | 1.1619014 | -1.2142423 | -3.8173203 | 0.7722614 | 0.2253 |
| bDensityYear[11] | -0.7864326 | 1.1651559 | -0.6748531 | -3.1518673 | 1.3770294 | 0.5040 |
| bDensityYear[12] | -0.2520908 | 1.1673984 | -0.2223446 | -2.6428958 | 1.8999666 | 0.8493 |
| bEfficiency | -1.7735459 | 0.1555540 | -11.3621426 | -2.0770923 | -1.4639251 | 0.0007 |
| bEfficiencyIndex | 0.1989810 | 0.4262533 | 0.4846959 | -0.6190535 | 1.0451957 | 0.6347 |
| bEfficiencyMarking | 0.1654221 | 0.1076543 | 1.5317465 | -0.0390752 | 0.3708288 | 0.1267 |
| bEfficiencyMarkingIndex | 1.6046481 | 0.4097403 | 3.9097275 | 0.8008554 | 2.3872085 | 0.0013 |
| sDensitySite | 0.6320314 | 0.0381650 | 16.5604943 | 0.5599186 | 0.7107649 | 0.0007 |
| sDispersion | 1.2761934 | 0.0677495 | 18.8599429 | 1.1517084 | 1.4189128 | 0.0007 |
| sEfficiencySwimmer | 0.4005182 | 0.1446675 | 2.9705127 | 0.2279183 | 0.7822507 | 0.0007 |
Table 3. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 3015 | 25 | 3 | 500 | 2 | 256 | 1.012 | TRUE |
Table 4. Summary survey information by year and river.
| Year | River | Sites | SurveyLength | SurveyPercent | Fish | Marked | Resighted |
|---|---|---|---|---|---|---|---|
| 2006 | Duncan | 0 | 0.0 | 0 | 0 | 0 | 0 |
| 2006 | Lardeau | 34 | 2.0 | 1 | 620 | 36 | 22 |
| 2007 | Duncan | 0 | 0.0 | 0 | 0 | 0 | 0 |
| 2007 | Lardeau | 47 | 2.7 | 2 | 260 | 0 | 0 |
| 2008 | Duncan | 0 | 0.0 | 0 | 0 | 0 | 0 |
| 2008 | Lardeau | 97 | 7.5 | 5 | 618 | 102 | 54 |
| 2009 | Duncan | 0 | 0.0 | 0 | 0 | 0 | 0 |
| 2009 | Lardeau | 83 | 5.0 | 4 | 390 | 0 | 0 |
| 2010 | Duncan | 0 | 0.0 | 0 | 0 | 0 | 0 |
| 2010 | Lardeau | 48 | 2.5 | 2 | 303 | 0 | 0 |
| 2011 | Duncan | 32 | 1.8 | 4 | 149 | 0 | 0 |
| 2011 | Lardeau | 264 | 15.8 | 11 | 1975 | 0 | 0 |
| 2012 | Duncan | 71 | 3.8 | 7 | 516 | 0 | 0 |
| 2012 | Lardeau | 257 | 15.2 | 11 | 1694 | 43 | 6 |
| 2013 | Duncan | 117 | 7.1 | 14 | 840 | 62 | 11 |
| 2013 | Lardeau | 308 | 18.0 | 13 | 1237 | 155 | 29 |
| 2014 | Duncan | 77 | 4.9 | 9 | 282 | 72 | 16 |
| 2014 | Lardeau | 273 | 16.3 | 12 | 1005 | 100 | 15 |
| 2016 | Duncan | 70 | 3.6 | 7 | 137 | 0 | 0 |
| 2016 | Lardeau | 257 | 14.7 | 10 | 321 | 16 | 3 |
| 2017 | Duncan | 92 | 5.5 | 11 | 255 | 30 | 5 |
| 2017 | Lardeau | 510 | 30.1 | 21 | 1370 | 29 | 0 |
| 2018 | Duncan | 19 | 1.0 | 2 | 34 | 0 | 0 |
| 2018 | Lardeau | 197 | 10.8 | 8 | 899 | 93 | 15 |
Table 5. Summary survey information by year.
| Year | Sites | SurveyLength | SurveyPercent | Fish | Marked | Resighted |
|---|---|---|---|---|---|---|
| 2006 | 34 | 2.0 | 1 | 620 | 36 | 22 |
| 2007 | 47 | 2.7 | 1 | 260 | 0 | 0 |
| 2008 | 97 | 7.5 | 4 | 618 | 102 | 54 |
| 2009 | 83 | 5.0 | 3 | 390 | 0 | 0 |
| 2010 | 48 | 2.5 | 1 | 303 | 0 | 0 |
| 2011 | 296 | 17.6 | 9 | 2124 | 0 | 0 |
| 2012 | 328 | 19.0 | 10 | 2210 | 43 | 6 |
| 2013 | 425 | 25.1 | 13 | 2077 | 217 | 40 |
| 2014 | 350 | 21.1 | 11 | 1287 | 172 | 31 |
| 2016 | 327 | 18.3 | 10 | 458 | 16 | 3 |
| 2017 | 602 | 35.6 | 19 | 1625 | 59 | 5 |
| 2018 | 216 | 11.8 | 6 | 933 | 93 | 15 |
Condition
Table 6. Parameter descriptions.
| Parameter | Description |
|---|---|
bWeight |
Intercept of log(eWeight) |
bWeightLength |
Intercept of effect of log(Length) on bWeight |
bWeightYear[i] |
Effect of ith Year on bWeight |
eWeight[i] |
Expected Weight of ith fish |
Length[i] |
Fork length of ith fish |
sWeight |
Log standard deviation of residual variation in log(Weight) |
sWeightYear |
Log standard deviation of bWeightYear |
Weight[i] |
Recorded weight of ith fish |
Year[i] |
Year ith fish was captured |
Table 7. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeight | -12.636773 | 0.2221935 | -56.88024 | -13.083567 | -12.207840 | 7e-04 |
| bWeightLength | 3.201633 | 0.0334451 | 95.73530 | 3.137294 | 3.268442 | 7e-04 |
| sWeight | -1.906158 | 0.0213756 | -89.16001 | -1.946579 | -1.861919 | 7e-04 |
| sWeightYear | -2.124485 | 0.1644743 | -12.86048 | -2.426690 | -1.781469 | 7e-04 |
Table 8. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 1113 | 4 | 3 | 500 | 2 | 350 | 1.007 | TRUE |
Fecundity
Table 9. Parameter descriptions.
| Parameter | Description |
|---|---|
bFecundity |
Intercept of eFecundity |
bFecundityWeight |
Effect of log(Weight) on log(bFecundity) |
eFecundity[i] |
Expected Fecundity of ith fish |
Fecundity[i] |
Fecundity of ith fish (eggs) |
sFecundity |
SD of residual variation in log(Fecundity) |
Weight[i] |
Weight of ith fish (mm) |
Table 10. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bFecundity | 3.9209077 | 0.9120282 | 4.098084 | 1.6821483 | 4.9494551 | 7e-04 |
| bFecundityWeight | 0.8598367 | 0.0328506 | 26.456045 | 0.8320117 | 0.9545648 | 7e-04 |
| sFecundity | 0.1272536 | 0.0206999 | 6.256100 | 0.0956913 | 0.1762694 | 7e-04 |
Table 11. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 22 | 3 | 3 | 500 | 2 | 248 | 1.007 | TRUE |
Egg Deposition
Table 12. The estimate total egg deposition by spawn year.
| Year | Length | Condition | Weight | Fecundity | Spawners | Eggs |
|---|---|---|---|---|---|---|
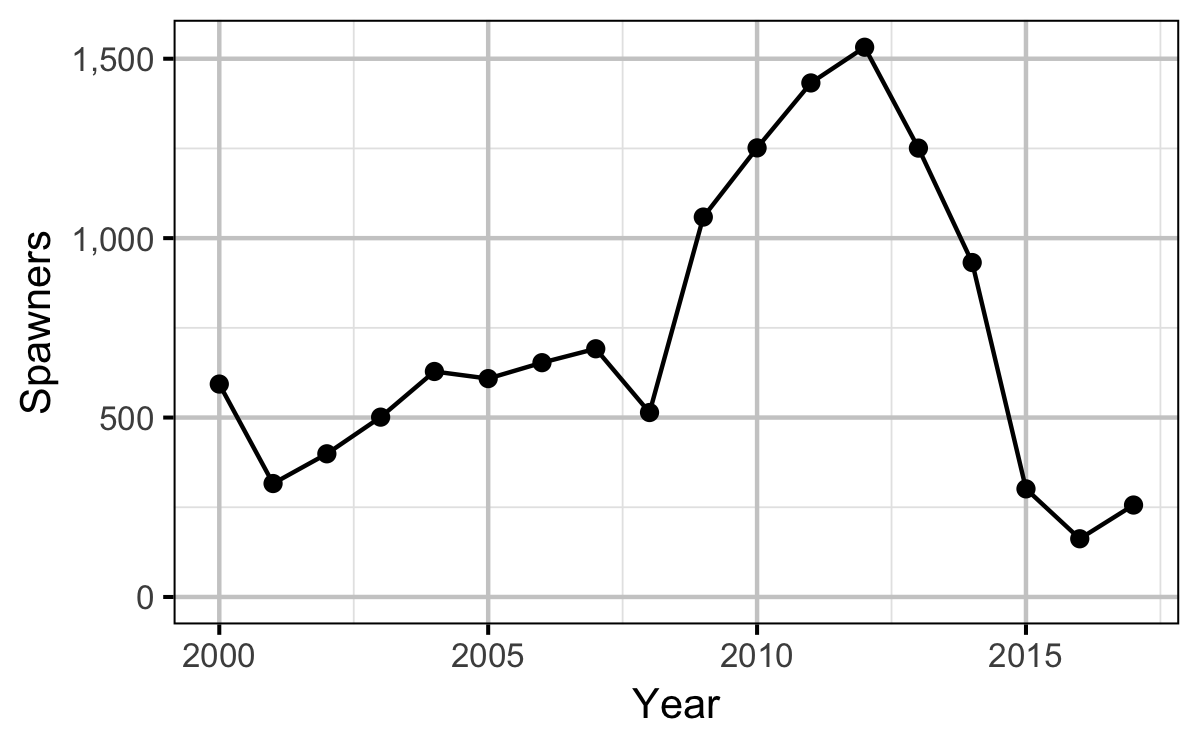
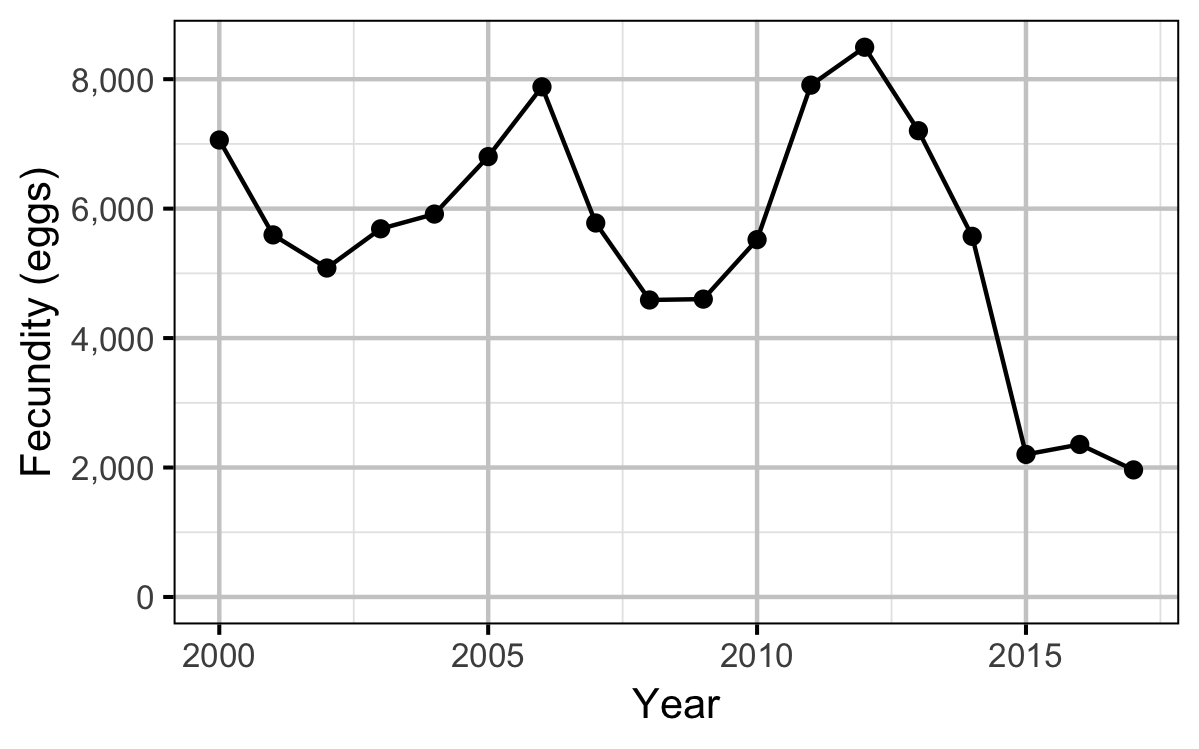
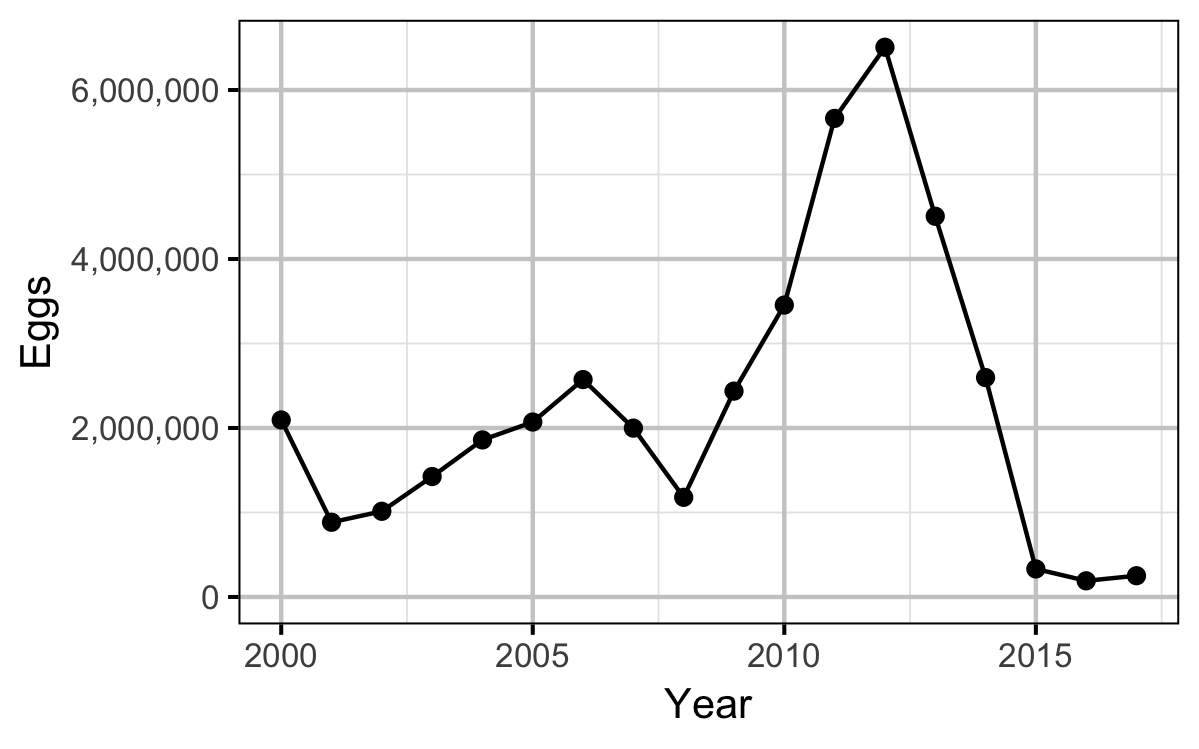
| 2000 | 780.1010 | 1.0393491 | 6139.137 | 7060.404 | 593.3613 | 2094685.3 |
| 2001 | 714.3372 | 1.0549815 | 4699.355 | 5594.193 | 316.1345 | 884258.6 |
| 2002 | 686.9467 | 1.0706139 | 4206.923 | 5082.432 | 398.9916 | 1013923.8 |
| 2003 | 712.0871 | 1.0862463 | 4789.665 | 5688.156 | 501.1765 | 1425384.9 |
| 2004 | 720.0000 | 1.0967083 | 5010.301 | 5916.112 | 628.4034 | 1858852.5 |
| 2005 | 770.0000 | 1.0387250 | 5884.646 | 6803.861 | 608.5714 | 2070317.8 |
| 2006 | 830.0000 | 0.9674553 | 6967.814 | 7881.746 | 652.9412 | 2573158.3 |
| 2007 | 739.8839 | 0.9783361 | 4876.891 | 5778.040 | 691.6807 | 1998279.2 |
| 2008 | 678.6507 | 0.9892170 | 3738.972 | 4588.655 | 514.0336 | 1179361.4 |
| 2009 | 669.5240 | 1.0363650 | 3751.517 | 4602.047 | 1058.7395 | 2436184.5 |
| 2010 | 730.0000 | 0.9693155 | 4628.480 | 5520.909 | 1251.5126 | 3454743.5 |
| 2011 | 810.8447 | 1.0463752 | 6994.031 | 7907.960 | 1432.5210 | 5664159.6 |
| 2012 | 854.1830 | 0.9616737 | 7594.224 | 8493.610 | 1532.0168 | 6506177.0 |
| 2013 | 828.6478 | 0.8769723 | 6283.148 | 7204.020 | 1250.9244 | 4505842.4 |
| 2014 | 780.0000 | 0.7922708 | 4677.790 | 5571.812 | 932.0168 | 2596511.3 |
| 2015 | 561.1913 | 0.7720349 | 1589.231 | 2202.325 | 301.2605 | 331736.8 |
| 2016 | 580.0000 | 0.7517990 | 1719.790 | 2356.435 | 162.1849 | 191089.0 |
| 2017 | 530.0000 | 0.8111756 | 1390.503 | 1963.320 | 256.2185 | 251519.4 |
Stock-Recruitment
Table 13. Parameter descriptions.
| Parameter | Description |
|---|---|
a |
Recruits per Stock at low density |
b |
Density-dependence |
eRecruits[i] |
Expected number of recruits from ith spawn year |
esRecruits[i] |
Expected SD of residual variation in Recruits |
Recruits[i] |
Number of recruits from ith spawn year |
SDLogRecruits[i] |
Standard deviation of uncertainty in log(Recruits[i]) |
sScaling |
Scaling term for SD of residual variation in log(eRecruits) |
Stock[i] |
Number of egg in ith spawn year |
All
Table 14. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| a | 0.6480776 | 0.2024845 | 3.199622 | 0.2624457 | 0.9850739 | 7e-04 |
| b | 0.0000057 | 0.0000024 | 2.435438 | 0.0000018 | 0.0000109 | 7e-04 |
| sScaling | 2.2045744 | 0.5784344 | 4.003556 | 1.4971373 | 3.7251551 | 7e-04 |
Table 15. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 12 | 3 | 3 | 500 | 100 | 1296 | 1.001 | TRUE |
Table 16. Estimated carry capacity (with 95% CRIs).
| estimate | lower | upper |
|---|---|---|
| 115000 | 77900 | 173000 |
Table 17. Estimated reference points (with 80% CRIs).
| Metric | estimate | lower | upper |
|---|---|---|---|
| eggs | 176000.00000 | 111000 | 356000.0000 |
| spawners | 58.66667 | 37 | 118.6667 |
Reduced
Table 18. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| a | 0.6821462 | 0.2008683 | 3.325851 | 0.288619 | 0.9829678 | 7e-04 |
| b | 0.0000061 | 0.0000025 | 2.517096 | 0.000002 | 0.0000113 | 7e-04 |
| sScaling | 2.1725201 | 0.5938579 | 3.854503 | 1.453242 | 3.8570925 | 7e-04 |
Table 19. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 11 | 3 | 3 | 500 | 100 | 1356 | 1.001 | TRUE |
Table 20. Estimated carry capacity (with 95% CRIs).
| estimate | lower | upper |
|---|---|---|
| 111000 | 76100 | 165000 |
Table 21. Estimated reference points (with 80% CRIs).
| Metric | estimate | lower | upper |
|---|---|---|---|
| eggs | 165000 | 106000.00000 | 326000.0000 |
| spawners | 55 | 35.33333 | 108.6667 |
Figures
Length Correction
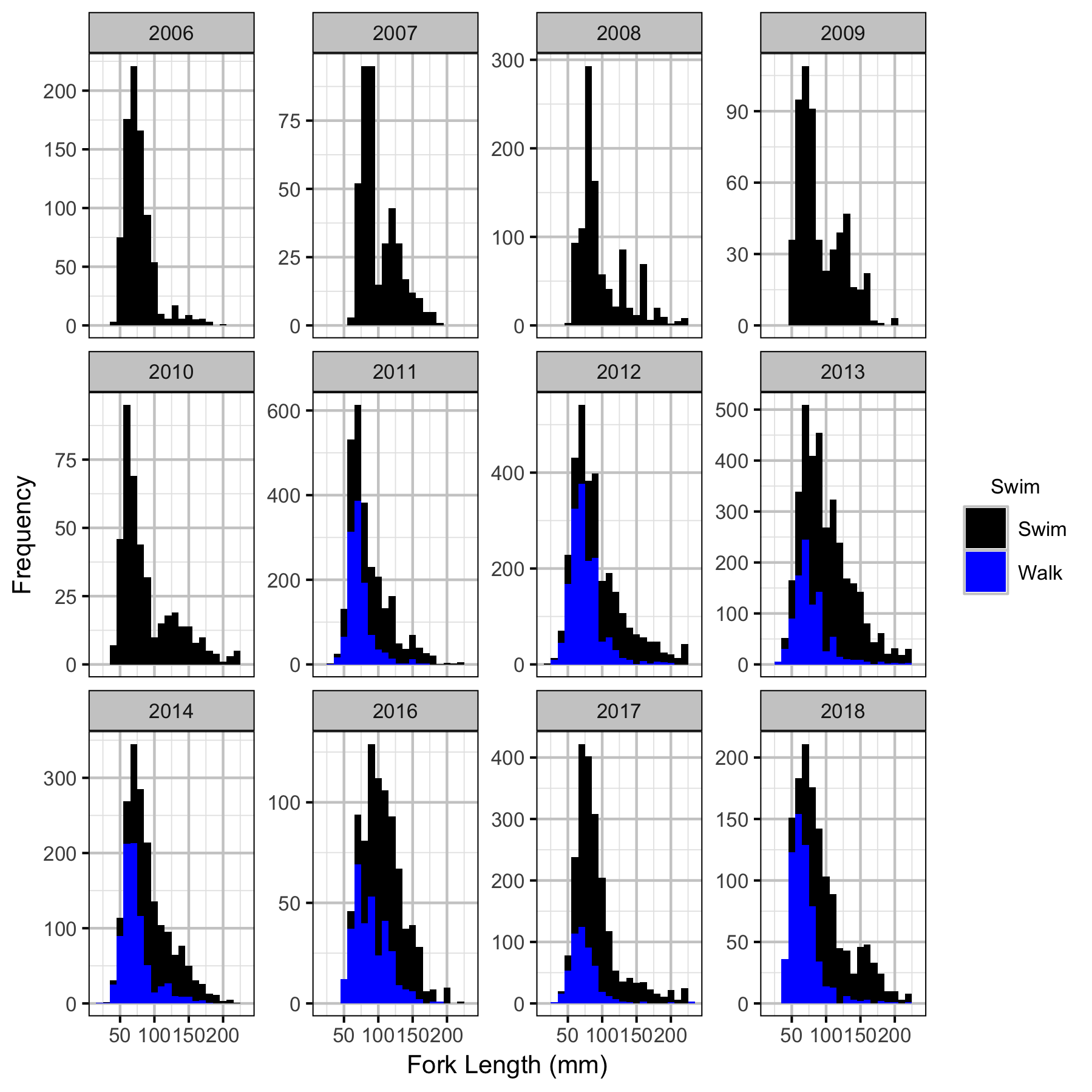
Abundance
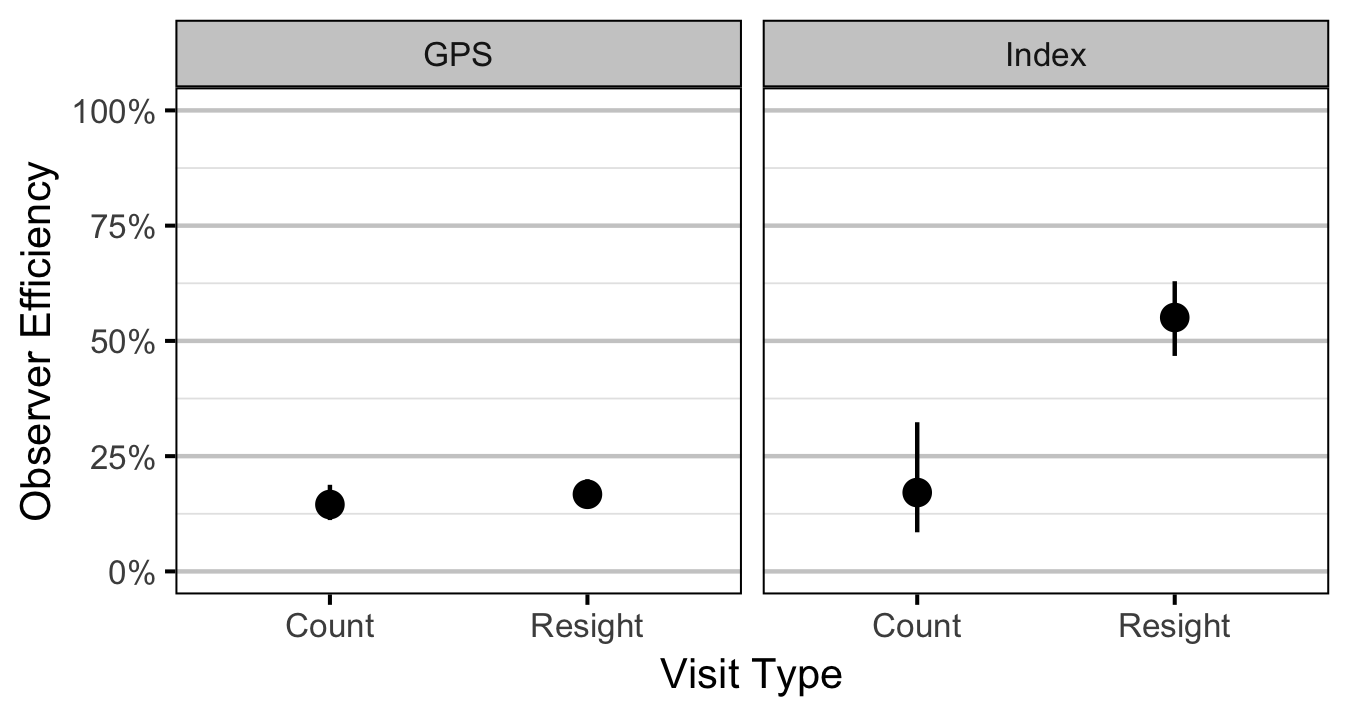
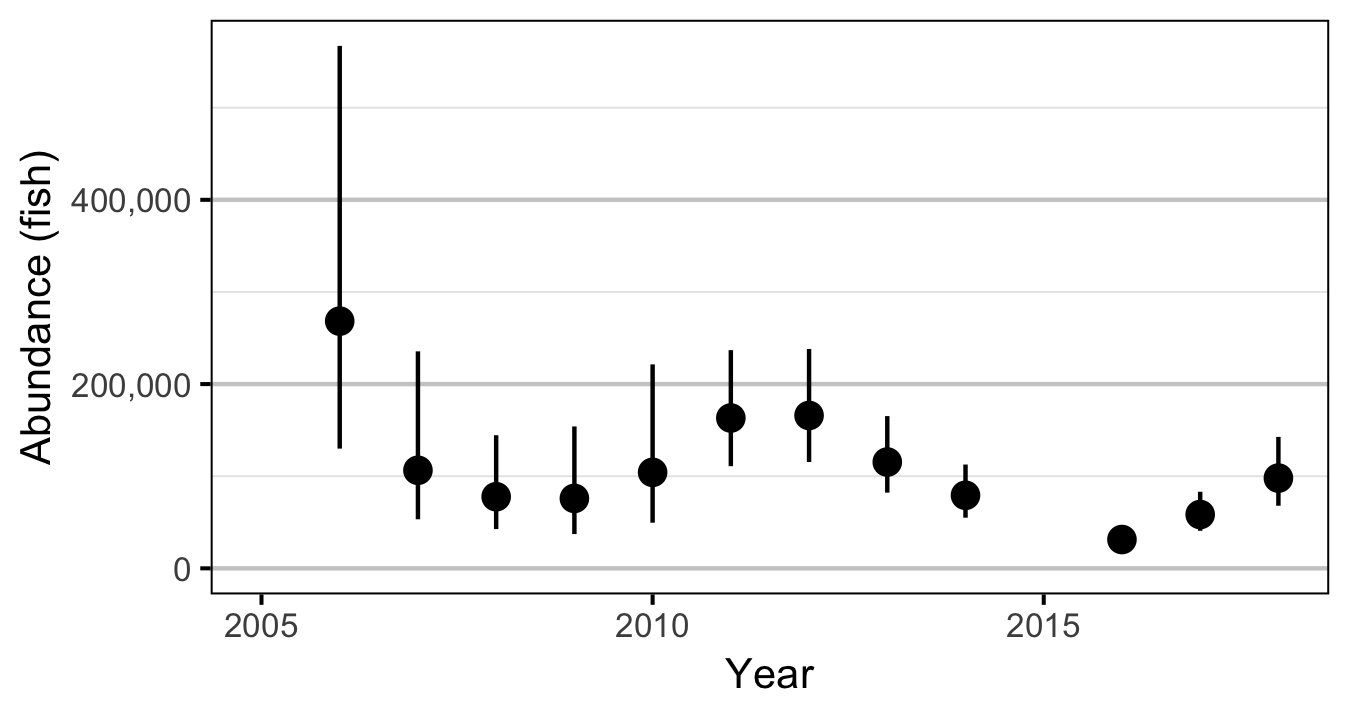
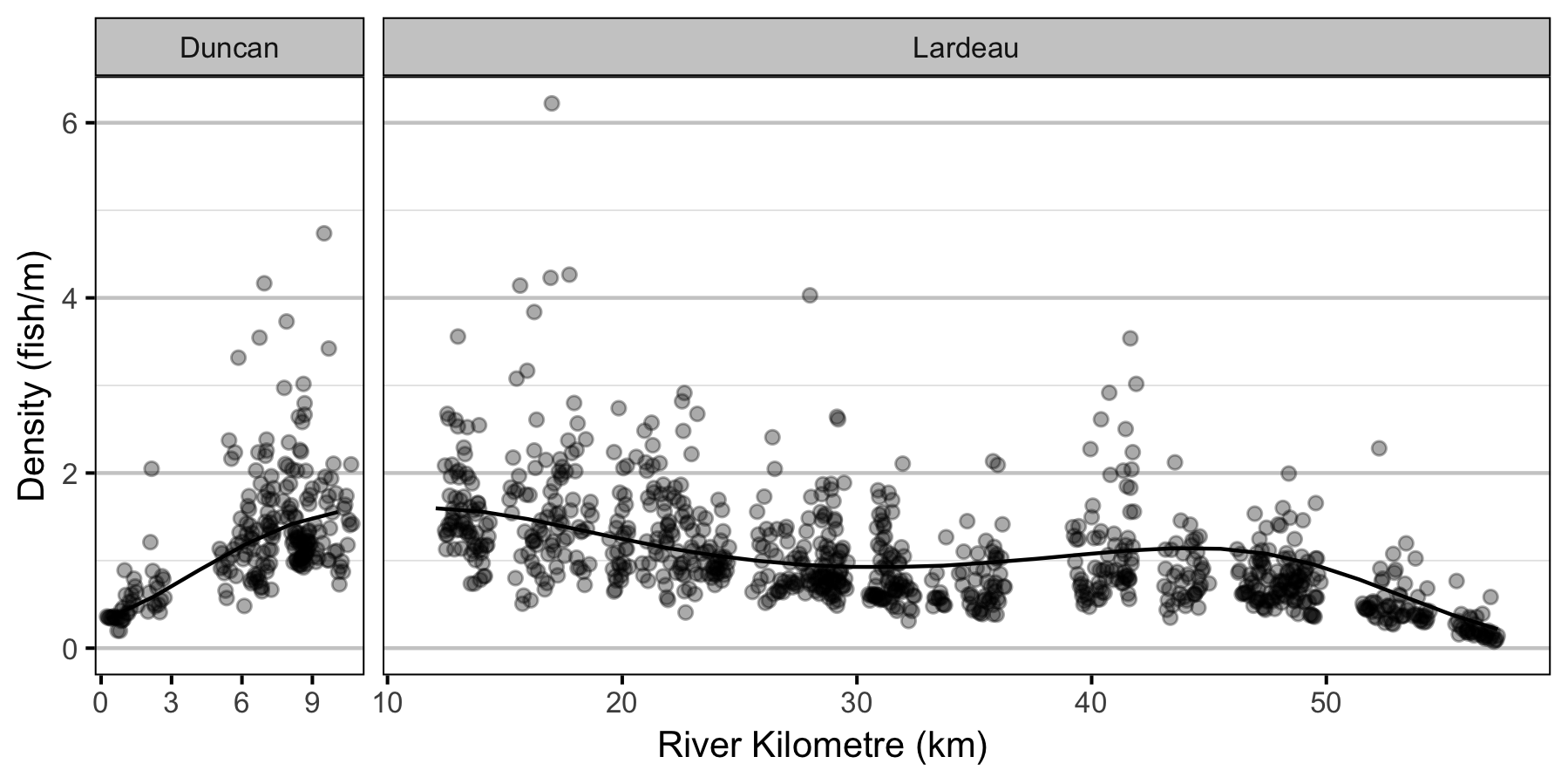
Condition
Fecundity
Spawner Size
Egg Deposition
Stock-Recruitment
Environmental
Reproductive Rate
Conclusions
- The Limit Reference Point is 356,000 eggs or 118 AUC spawners (based on fecundity in a typical year).
- The egg deposition has fallen below the LRP since 2015.
- Exclusion of the large recruitment estimate from the 2005 spawn year has little effect on the estimates of the LRP.
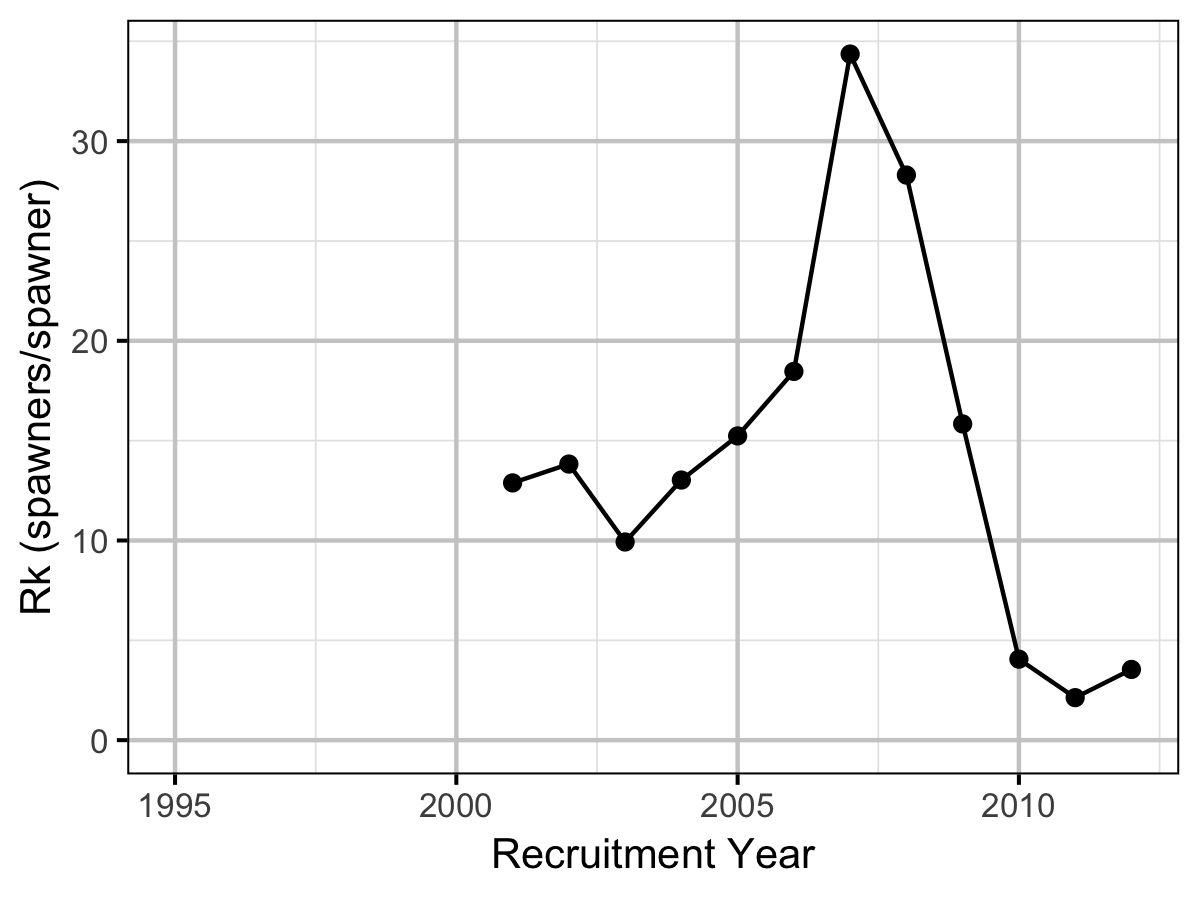
- The maximum reproductive rate increased from around 12.5 in the early to mid 2000s to over 30 in 2007 before dropping to under 5 in 2010. The changes reflect shifts in the inlake survival.
Recommendations
- Develop a Limit Reference Point that ensures a effective population size (\(N_e\)) of 500.
- Develop an Upper Reference Point that ensures adequate Kokanee recruitment.
Acknowledgements
The organisations and individuals whose contributions have made this analysis report possible include:
- Habitat Conservation Trust Foundation (HCTF) and the anglers, hunters, trappers and guides who contribute to the Trust.
- Fish and Wildlife Compensation Program (FWCP) and its program partners BC Hydro, the Province of BC and Fisheries and Oceans Canada.
- Ministry of Forests, Lands and Natural Resource
Operations (MFLNRO)
- Greg Andrusak
- Matt Neufeld
- Jeff Burrows
- Tyler Weir
- Rob Bison
- Stefan Himmer
- Vicky Lipinski
- John Hagen
- Scott Decker
- Jody Schick
- Gillian Sanders
- Jeremy Baxter
- Jeff Berdusco
- Dave Derosa
- Seb Dalgarno