Kaslo Bull Trout Productivity Analysis 2016
The suggested citation for this analytic report is:
Thorley, J.L. and Hogan P.M. (2017) Kaslo Bull Trout Productivity Analysis 2016. A Poisson Consulting Analysis Report. URL: https://www.poissonconsulting.ca/f/1827953676.
Background
The Kaslo River and Keen Creek, which is a tributary of the Kaslo River, are important Bull Trout spawning and rearing tributaries on Kootenay Lake. From 2012 to 2016, field crews have night-snorkeled both systems in the fall and recorded all juvenile Bull Trout between 30 mm and 350 mm in length. Snorkel and electrofishing marking crews have also captured and tagged juvenile Bull Trout for the snorkel crews to resight. Redd counts have been conducted in both systems since 2006.
The primary goal of the current analyses is to answer the following questions:
What is the observer efficiency when night-snorkeling for juvenile Bull Trout in the Kaslo River and Keen Creek?
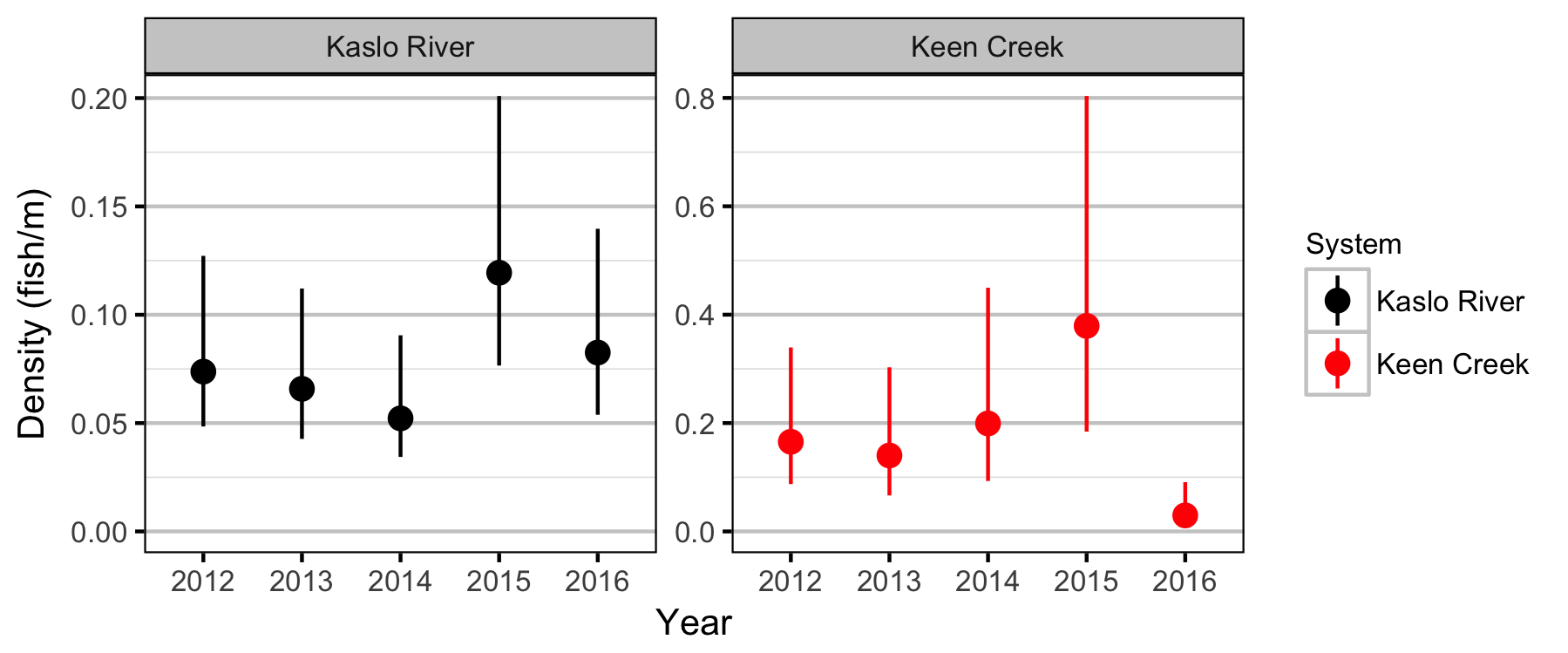
What are the densities of age-1 Bull Trout in the Kaslo River and Keen Creek?
What is the relationship between the number of redds and the resultant densities of age-1 Bull Trout two years later?
Data Preparation
The data were provided in the form of clean and tidy Excel spreadsheets by Gary Pavan and prepared for analysis using R version 3.3.2 (R Core Team 2015).
Table 1. Bull Trout length cutoffs by age-class.
| Age Class | Length (mm) |
|---|---|
| Age-0 | 30 - 90 |
| Age-1 | 91 - 150 |
| Age-2+ | 151 - 350 |
Statistical Analysis
Model parameters were estimated using Maximum-Likelihood (ML) and Bayesian methods. The Maximum-Likelihood Estimates (MLE) were obtained using TMB (Kristensen et al. 2016) while the Bayesian estimates were produced using JAGS (Plummer 2015). For additional information on ML estimation the reader is referred to Millar (2011). For additional information on Bayesian modelling in the BUGS language, of which JAGS uses a dialect, the reader is referred to Kery and Schaub (2011).
Unless indicated otherwise, the Bayesian analyses used uninformative normal prior distributions (Kery and Schaub 2011, 36). The posterior distributions were estimated from 2,000 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of four chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that \(\hat{R} < 1.1\) (Kery and Schaub 2011, 40) for each of the monitored parameters (Kery and Schaub 2011, 61).
The parameters are summarised in terms of the point estimate, standard deviation (sd), the z-score, lower and upper 95% confidence/credible limits (CLs) and the p-value (Kery and Schaub 2011, 37, 42). For ML models, the point estimate is the MLE, the standard deviation is the standard error, the z-score is \(\mathrm{sd}/\mathrm{MLE}\) and the 95% CLs are the \(\mathrm{MLE} \pm 1.96 \cdot \mathrm{sd}\). A p-value of 0.05 indicates that the lower or upper 95% CL is 0. For Bayesian models, the estimate is the median (50th percentile) of the MCMC samples, the z-score is \(\mathrm{mean}/\mathrm{sd}\) and the 95% CLs are the 2.5th and 97.5th percentiles.
The support for fixed terms in ML models with identical random (Kery and Schaub 2011, 75) effects was assessed using Akaike’s weights (\(w_i\)) calculated from the marginal Akaike’s Information Criterion corrected for small sample size (AICc, Burnham and Anderson 2002). The Akaike’s weights were used for model averaging (Burnham and Anderson 2002). The fixed terms with low support were dropped from the final Bayesian model.
Where relevant, model adequacy was confirmed by examination of residual plots for the full model(s).
The results are displayed graphically by plotting the modeled relationships between particular variables and the response(s) with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values, respectively, while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). When informative the influence of particular variables is expressed in terms of the effect size (i.e., percent change in the response variable) with 95% confidence/credible intervals (CIs, Bradford, Korman, and Higgins 2005).
The analyses were implemented using R version 3.3.2
(R Core Team 2015) and the tmbr and jmbr packages.
Model Descriptions
Observer Efficiency
All resighted fish with a tag were allocated to the closest unallocated marked fish (with the same colour tag) by fork length and distance. The marked fish were analysed using a logistic regression model. Key assumptions of the full Maximum Likelihood logistic regression include:
- The observer efficiency varies by the fork length as a second order polynomial.
- The observer efficiency varies between systems.
- The observer efficiency varies by the gradient, sinuosity and watershed area.
The final Bayesian logistic regression assumed that:
- The observer efficiency varies by the fork length.
Lineal Density
Both systems were broken into 100 m sites by bank. The lineal density at each site was estimated using an over-dispersed Poisson Generalized Linear Mixed Model. Key assumptions of the full Maximum Likelihood GLMM include:
- The lineal density varies between systems and years.
- The lineal density varies randomly by site.
- The lineal density varies by site sinuosity, gradient and watershed area.
- The observer efficiency for each system is as estimated by the observer efficiency model.
The final Bayesian GLMM dropped sinuosity and gradient and took into account the uncertainty in the observer efficiencies as estimated by the observer efficiency model.
Stock-Recruitment
The stock-recruitment relationship was estimated using a Bayesian Beverton-Holt stock-recruitment curve. Key assumptions of the final BH SR model include:
- The strength of density-dependence varies between systems.
Model Templates
Observer Efficiency
Maximum Likelihood
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() () {
DATA_VECTOR(Observed);
DATA_FACTOR(System);
DATA_VECTOR(Tagged);
DATA_VECTOR(Length);
DATA_VECTOR(Gradient);
DATA_VECTOR(Sinuosity);
DATA_VECTOR(Area);
PARAMETER(bIntercept);
PARAMETER(bSystem);
PARAMETER(bLength);
PARAMETER(bLength2);
PARAMETER(bGradient);
PARAMETER(bSinuosity);
PARAMETER(bArea);
vector<Type> eObserved = Observed;
int n = Observed.size();
Type nll = 0.0;
for(int i = 0; i < n; i++){
eObserved(i) = invlogit(bIntercept + bSystem * System(i) + bLength * Length(i) + bLength2 * pow(Length(i), 2) + bGradient * Gradient(i) + bSinuosity * Sinuosity(i) + bArea * Area(i));
nll -= dbinom(Observed(i), Tagged(i), eObserved(i), true);
return nll;
..Template 1. Full model.
Bayesian
model{
bIntercept ~ dnorm(0, 5^-2)
bLength ~ dnorm(0, 5^-2)
for(i in 1:length(Observed)){
logit(eObserved[i]) <- bIntercept + bLength * Length[i]
Observed[i] ~ dbern(eObserved[i])
}
..Template 2. Final model.
Lineal Density
Maximum Likelihood
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() () {
DATA_VECTOR(Count);
DATA_VECTOR(Length);
DATA_VECTOR(Coverage);
DATA_VECTOR(Efficiency);
DATA_VECTOR(Dispersion);
DATA_VECTOR(Gradient);
DATA_VECTOR(Sinuosity);
DATA_VECTOR(Area);
DATA_FACTOR(System);
DATA_FACTOR(Site);
DATA_INTEGER(nSite);
DATA_FACTOR(Year);
PARAMETER_MATRIX(bSystemYear);
PARAMETER_VECTOR(bSite);
PARAMETER(bGradient);
PARAMETER(bSinuosity);
PARAMETER(bArea);
PARAMETER_VECTOR(bDispersion);
DATA_INTEGER(nDispersion);
PARAMETER(log_sDispersion);
PARAMETER(log_sSite);
Type sSite = exp(log_sSite);
Type sDispersion = exp(log_sDispersion);
ADREPORT(sSite);
ADREPORT(sDispersion);
vector<Type> eDensity = Count;
vector<Type> eCount = Count;
vector<Type> eNorm = pnorm(bDispersion, Type(0), Type(1));
vector<Type> eDispersion = qgamma(eNorm, pow(sDispersion, -2), pow(sDispersion, 2));
Type nll = 0.0;
for(int i = 0; i < nSite; i++){
nll -= dnorm(bSite(i), Type(0), sSite, true);
}
for(int i = 0; i < nDispersion; i++){
nll -= dnorm(bDispersion(i), Type(0), Type(1), true);
eDensity(i) = exp(bSystemYear(System(i), Year(i)) + bGradient * Gradient(i) + bSinuosity * Sinuosity(i) + bArea * Area(i) + bSite(Site(i)));
eCount(i) = eDensity(i) * Length(i) * Coverage(i);
nll -= dpois(Count(i), eCount(i) * Efficiency(i) * eDispersion(i), true);
}
return nll;
}Template 3. The full model.
Bayesian
model{
bEfficiency ~ dnorm(Efficiency[1], EfficiencySD[1]^-2) T(0, )
for(i in 1:nSystem) {
for(j in 1:nYear) {
bSystemYear[i,j] ~ dnorm(0, 5^-2)
}
}
log_sSite ~ dnorm(0, 5^-2)
log(sSite) <- log_sSite
for(i in 1:nSite) {
bSite[i] ~ dnorm(0, sSite^-2)
}
bArea ~ dnorm(0, 5^-2)
log_sDispersion ~ dnorm(0, 5^-2)
log(sDispersion) <- log_sDispersion
for(i in 1:length(Count)) {
log(eDensity[i]) <- bSystemYear[System[i],Year[i]] + bArea * Area[i] + bSite[Site[i]]
eDispersion[i] ~ dgamma(sDispersion^-2, sDispersion^-2)
Count[i] ~ dpois(eDensity[i] * Length[i] * Coverage[i] * bEfficiency * eDispersion[i])
}
..Template 4. The final model.
Stock-Recruiment
model {
log_bAlpha ~ dnorm(5, 5^-2)
log(bAlpha) <- log_bAlpha
for(i in 1:nSystem) {
log_bBeta[i] ~ dnorm(0, 5^-2)
log(bBeta[i]) <- log_bBeta[i]
}
log_sRecruits ~ dnorm(0, 5^-2)
log(sRecruits) <- log_sRecruits
for(i in 1:length(Recruits)){
eRecruits[i] <- bAlpha * Stock[i] / (1 + bBeta[System[i]] * Stock[i])
Recruits[i] ~ dlnorm(log(eRecruits[i]), sRecruits^-2)
}
bCarryingCapacity <- bAlpha / bBeta
..Template 5. Final model.
Results
Tables
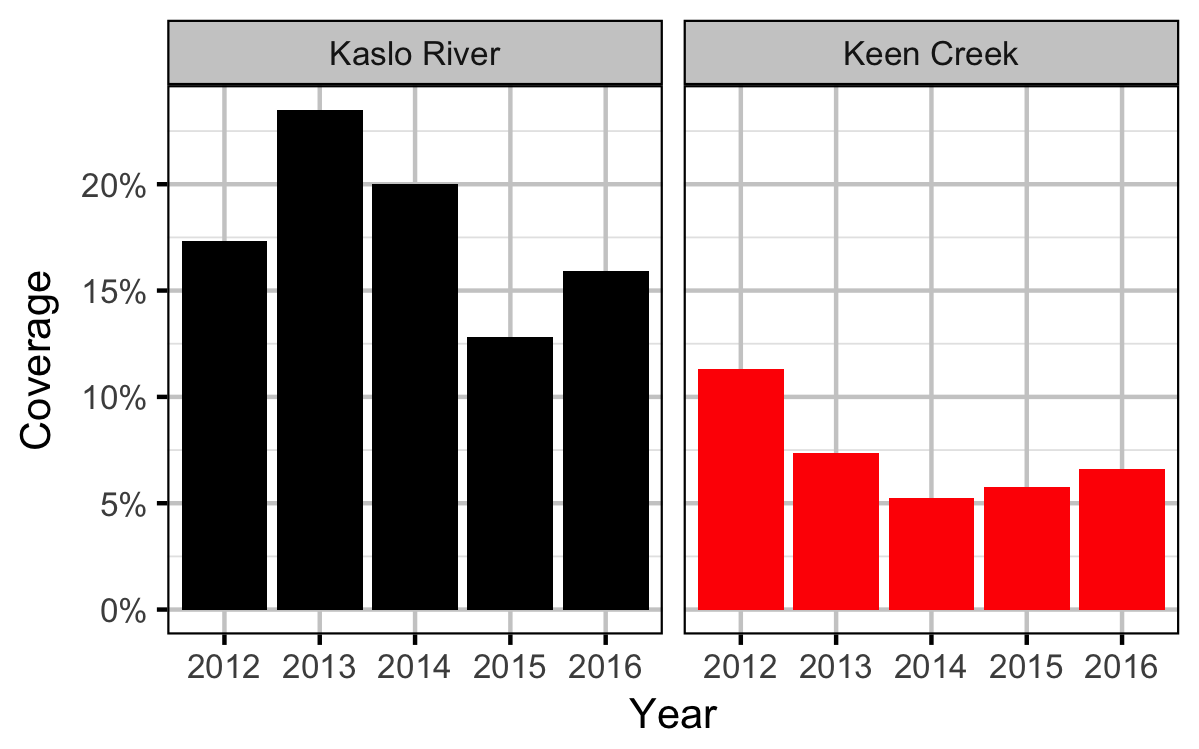
Coverage
Table 2. Total length of river bank counted (including replicates) by system and year.
| System | Year | Length (km) |
|---|---|---|
| Kaslo River | 2012 | 10.60 |
| Kaslo River | 2013 | 13.44 |
| Kaslo River | 2014 | 11.45 |
| Kaslo River | 2015 | 7.33 |
| Kaslo River | 2016 | 11.58 |
| Keen Creek | 2012 | 1.44 |
| Keen Creek | 2013 | 0.95 |
| Keen Creek | 2014 | 0.67 |
| Keen Creek | 2015 | 0.75 |
| Keen Creek | 2016 | 0.85 |
Fish
Table 3. Number of fish observed by system, age-class and species. All species are assumed to have the Bull Trout age-class length cutoffs.
| System | AgeClass | Year | Bull Trout | Brook Trout | Rainbow Trout |
|---|---|---|---|---|---|
| Kaslo River | Age-0 | 2012 | 104 | 0 | 1 |
| Kaslo River | Age-0 | 2013 | 104 | 1 | 41 |
| Kaslo River | Age-0 | 2014 | 253 | 1 | 49 |
| Kaslo River | Age-0 | 2015 | 89 | 1 | 33 |
| Kaslo River | Age-0 | 2016 | 187 | 4 | 138 |
| Kaslo River | Age-1 | 2012 | 151 | 2 | 86 |
| Kaslo River | Age-1 | 2013 | 161 | 12 | 63 |
| Kaslo River | Age-1 | 2014 | 113 | 10 | 66 |
| Kaslo River | Age-1 | 2015 | 166 | 3 | 81 |
| Kaslo River | Age-1 | 2016 | 172 | 20 | 277 |
| Kaslo River | Age-2+ | 2012 | 173 | 29 | 205 |
| Kaslo River | Age-2+ | 2013 | 196 | 14 | 174 |
| Kaslo River | Age-2+ | 2014 | 207 | 21 | 140 |
| Kaslo River | Age-2+ | 2015 | 69 | 3 | 61 |
| Kaslo River | Age-2+ | 2016 | 114 | 4 | 188 |
| Keen Creek | Age-0 | 2012 | 8 | 0 | 0 |
| Keen Creek | Age-0 | 2013 | 4 | 0 | 0 |
| Keen Creek | Age-0 | 2014 | 8 | 0 | 0 |
| Keen Creek | Age-0 | 2015 | 2 | 1 | 4 |
| Keen Creek | Age-0 | 2016 | 1 | 0 | 0 |
| Keen Creek | Age-1 | 2012 | 40 | 0 | 3 |
| Keen Creek | Age-1 | 2013 | 20 | 0 | 0 |
| Keen Creek | Age-1 | 2014 | 21 | 0 | 1 |
| Keen Creek | Age-1 | 2015 | 43 | 0 | 4 |
| Keen Creek | Age-1 | 2016 | 4 | 0 | 0 |
| Keen Creek | Age-2+ | 2012 | 88 | 1 | 24 |
| Keen Creek | Age-2+ | 2013 | 61 | 3 | 10 |
| Keen Creek | Age-2+ | 2014 | 42 | 0 | 7 |
| Keen Creek | Age-2+ | 2015 | 40 | 2 | 9 |
| Keen Creek | Age-2+ | 2016 | 19 | 1 | 10 |
Observer Efficiency
Table 4. Parameter descriptions.
| Parameter | Description |
|---|---|
Area |
The standardized watershed area |
bArea |
The effect of Area on bIntercept |
bGradient |
The effect of Gradient on bIntercept |
bIntercept |
The intercept for logit(eObserved) |
bLength |
The effect of Length on bIntercept |
bLength2 |
The effect of Length on the effect of Length on bIntercept |
bSinuosity |
The effect of Sinuosity on bIntercept |
eObserved |
The expected probability of observing an individual |
Gradient |
The standardized site-level gradient |
Length |
The standardized fork length |
Observed |
The number of individuals observed (0 or 1) |
Sinuosity |
The standardized site-level sinuosity |
Tagged |
The number of tagged individuals (1) |
Maximum Likelihood
Table 5. Model averaged parameter estimates and Akaike weights.
| term | estimate | lower | upper | AICcWt | proportion |
|---|---|---|---|---|---|
| bArea | -0.0017069 | -0.1006719 | 0.0972580 | 0.28 | 0.5000000 |
| bGradient | 0.1106604 | -0.0519700 | 0.2732909 | 0.49 | 0.5000000 |
| bIntercept | -1.3347658 | -1.7671369 | -0.9023946 | 1.00 | 1.0000000 |
| bLength | 0.7882196 | 0.3642009 | 1.2122382 | 1.00 | 0.6666667 |
| bLength2 | -0.0204026 | -0.1335130 | 0.0927077 | 0.29 | 0.3333333 |
| bSinuosity | -0.0171433 | -0.1192925 | 0.0850059 | 0.29 | 0.5000000 |
| bSystem | 0.0734957 | -0.2092507 | 0.3562421 | 0.32 | 0.5000000 |
Bayesian
Table 6. Final parameter estimates.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bIntercept | -1.3192427 | 0.1927530 | -6.867853 | -1.7127948 | -0.9460519 | 5e-04 |
| bLength | 0.8178457 | 0.2035919 | 4.016946 | 0.4389397 | 1.2481336 | 5e-04 |
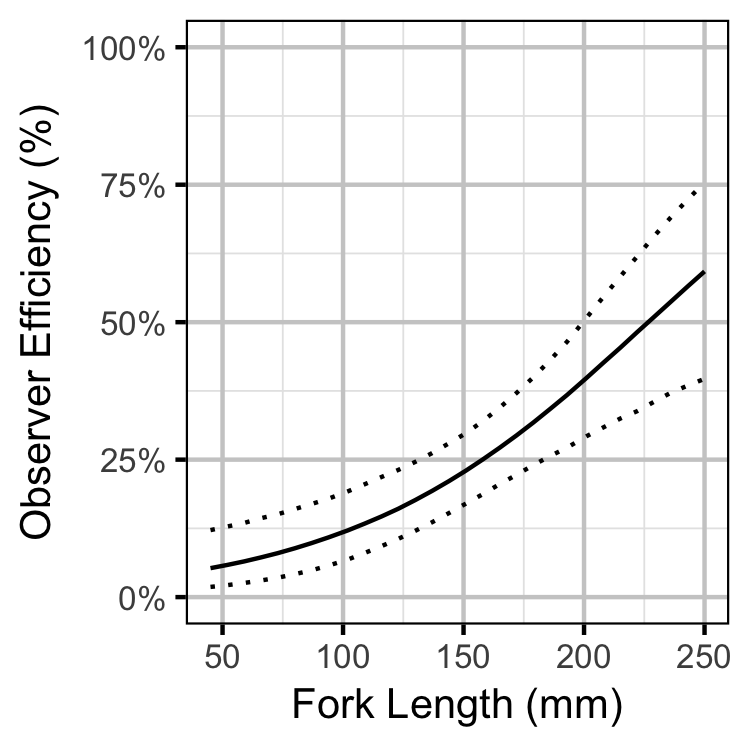
Table 7. Observer Efficiency estimates for a 123 mm Bull Trout.
| System | Efficiency | EfficiencySD | EfficiencyLower | EfficiencyUpper |
|---|---|---|---|---|
| Kaslo River | 0.1608607 | 0.0318899 | 0.106091 | 0.2314487 |
Table 8. Final model summary.
| n | K | nsims | minutes | rhat | converged |
|---|---|---|---|---|---|
| 190 | 2 | 4000 | 0 | 1 | TRUE |
Lineal Density
Table 9. Parameter descriptions.
| Parameter | Description |
|---|---|
Area |
Standardized water shed area |
bArea |
The effect of Area on bSystemYear |
bDispersion |
The random effect of overdispersion |
bGradient |
The effect of Gradient on bSystemYear |
bSinuosity |
The effect of Sinuosity on bSystemYear |
bSite |
The random effect of Site on bSystemYear |
bSystemYear |
The effect of System and Year on log(eDensity) |
Count |
Number of fish counted |
Coverage |
Proportion of site surveyed |
Dispersion |
Factor for random effect of overdispersion |
eCount |
The expected Count |
eDensity |
The expected lineal density |
Efficiency |
The observer efficiency from the observer efficiency model |
Gradient |
Standardized gradient |
Length |
Length of site (m) |
log_sDispersion |
log(sDispersion) |
log_sSite |
log(sSite) |
sDispersion |
The SD of bDispersion |
Sinuosity |
Standardized sinuosity |
Site |
The site |
sSite |
The SD of bSite |
System |
The system |
Year |
The year |
Maximum Likelihood
Table 10. Model averaged parameter estimates and Akaike weights.
| term | estimate | lower | upper | AICcWt | proportion |
|---|---|---|---|---|---|
| bArea | -0.2739053 | -0.3895691 | -0.1582416 | 1.00 | 0.5 |
| bGradient | 0.0097758 | -0.0231209 | 0.0426726 | 0.29 | 0.5 |
| bSinuosity | 0.0059621 | -0.0228655 | 0.0347898 | 0.28 | 0.5 |
| bSystemYear[1,1] | -2.6841871 | -2.9197896 | -2.4485847 | 1.00 | 1.0 |
| bSystemYear[2,1] | -1.8876568 | -2.3826415 | -1.3926720 | 1.00 | 1.0 |
| bSystemYear[1,2] | -2.7906519 | -3.0019628 | -2.5793410 | 1.00 | 1.0 |
| bSystemYear[2,2] | -2.0803353 | -2.7264547 | -1.4342159 | 1.00 | 1.0 |
| bSystemYear[1,3] | -3.0161576 | -3.2530276 | -2.7792875 | 1.00 | 1.0 |
| bSystemYear[2,3] | -1.7101188 | -2.3955810 | -1.0246565 | 1.00 | 1.0 |
| bSystemYear[1,4] | -2.2101955 | -2.4658209 | -1.9545702 | 1.00 | 1.0 |
| bSystemYear[2,4] | -1.0707215 | -1.6717979 | -0.4696451 | 1.00 | 1.0 |
| bSystemYear[1,5] | -2.5681359 | -2.7869987 | -2.3492732 | 1.00 | 1.0 |
| bSystemYear[2,5] | -3.5979138 | -4.6988262 | -2.4970014 | 1.00 | 1.0 |
| log_sDispersion | -0.6021288 | -0.8760902 | -0.3281674 | 1.00 | 1.0 |
| log_sSite | -0.7461595 | -1.0708793 | -0.4214397 | 1.00 | 1.0 |
Bayesian
Table 11. Parameter estimates.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bArea | -0.2781154 | 0.0621234 | -4.457202 | -0.3956392 | -0.1515780 | 0.0005 |
| bEfficiency | 0.1512070 | 0.0308545 | 4.926864 | 0.0944904 | 0.2154814 | 0.0005 |
| bSystemYear[1,1] | -2.6069882 | 0.2473494 | -10.481034 | -3.0274515 | -2.0621505 | 0.0005 |
| bSystemYear[2,1] | -1.7989467 | 0.3431898 | -5.223380 | -2.4376257 | -1.0802347 | 0.0005 |
| bSystemYear[1,2] | -2.7208528 | 0.2432920 | -11.135057 | -3.1532978 | -2.1882643 | 0.0005 |
| bSystemYear[2,2] | -1.9649135 | 0.3893722 | -5.040127 | -2.7114989 | -1.1942871 | 0.0005 |
| bSystemYear[1,3] | -2.9530350 | 0.2449763 | -11.986879 | -3.3699672 | -2.4021859 | 0.0005 |
| bSystemYear[2,3] | -1.6130127 | 0.4145783 | -3.852310 | -2.3741468 | -0.7991154 | 0.0005 |
| bSystemYear[1,4] | -2.1254128 | 0.2492309 | -8.481387 | -2.5697905 | -1.6046600 | 0.0005 |
| bSystemYear[2,4] | -0.9694249 | 0.3697839 | -2.608590 | -1.6914508 | -0.2187118 | 0.0110 |
| bSystemYear[1,5] | -2.4942010 | 0.2358466 | -10.525699 | -2.9214561 | -1.9683893 | 0.0005 |
| bSystemYear[2,5] | -3.5201812 | 0.6061670 | -5.861660 | -4.8402786 | -2.3976574 | 0.0005 |
| log_sDispersion | -0.5201483 | 0.1416584 | -3.755881 | -0.8548630 | -0.2877524 | 0.0005 |
| log_sSite | -0.7622263 | 0.1902390 | -4.121403 | -1.2164673 | -0.4589483 | 0.0005 |
Table 12. Model summary.
| n | K | nsims | minutes | rhat | converged |
|---|---|---|---|---|---|
| 635 | 14 | 40000 | 1 | 1.02 | TRUE |
Stock-Recruiment
Table 13. Parameter descriptions.
| Parameter | Description |
|---|---|
bBeta |
Density-dependence |
eRecruits |
Expected value of Recruits |
Recruits |
Number of age-1 Bull Trout |
Stock |
Number of Bull Trout redds |
bAlpha |
Recruits per stock at low stock density |
sRecruits |
SD of residual variation in Recruits |
Bayesian
Table 14. Final parameter estimates.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bAlpha | 55.1638659 | 2.317486e+03 | 0.2003459 | 26.0909448 | 5.252221e+03 | 0.0005 |
| bBeta[1] | 0.2625295 | 1.247149e+01 | 0.2056719 | 0.0490347 | 2.955343e+01 | 0.0005 |
| bBeta[2] | 0.0324063 | 8.465149e+00 | 0.1691144 | 0.0000199 | 1.597592e+01 | 0.0005 |
| bCarryingCapacity[1] | 217.1207958 | 7.792184e+02 | 0.3637510 | 105.0475478 | 6.354322e+02 | 0.0005 |
| bCarryingCapacity[2] | 1491.5964691 | 1.659590e+07 | 0.0533275 | 233.9749651 | 1.824370e+06 | 0.0005 |
| log_bAlpha | 4.0103081 | 1.179864e+00 | 3.6926391 | 3.2615875 | 8.566406e+00 | 0.0005 |
| log_bBeta[1] | -1.3373921 | 1.396203e+00 | -0.7652314 | -3.0152327 | 3.386143e+00 | 0.2650 |
| log_bBeta[2] | -3.4294052 | 3.114748e+00 | -1.2139894 | -10.8255300 | 2.771066e+00 | 0.1650 |
| log_sRecruits | -0.5451263 | 2.752378e-01 | -1.8820430 | -0.9897406 | 8.341750e-02 | 0.0800 |
| sRecruits | 0.5797686 | 1.892507e-01 | 3.2757911 | 0.3716731 | 1.086996e+00 | 0.0005 |
Table 15. Final model summary.
| n | K | nsims | minutes | rhat | converged |
|---|---|---|---|---|---|
| 10 | 10 | 16000 | 0 | 1.06 | TRUE |
Figures
Systems
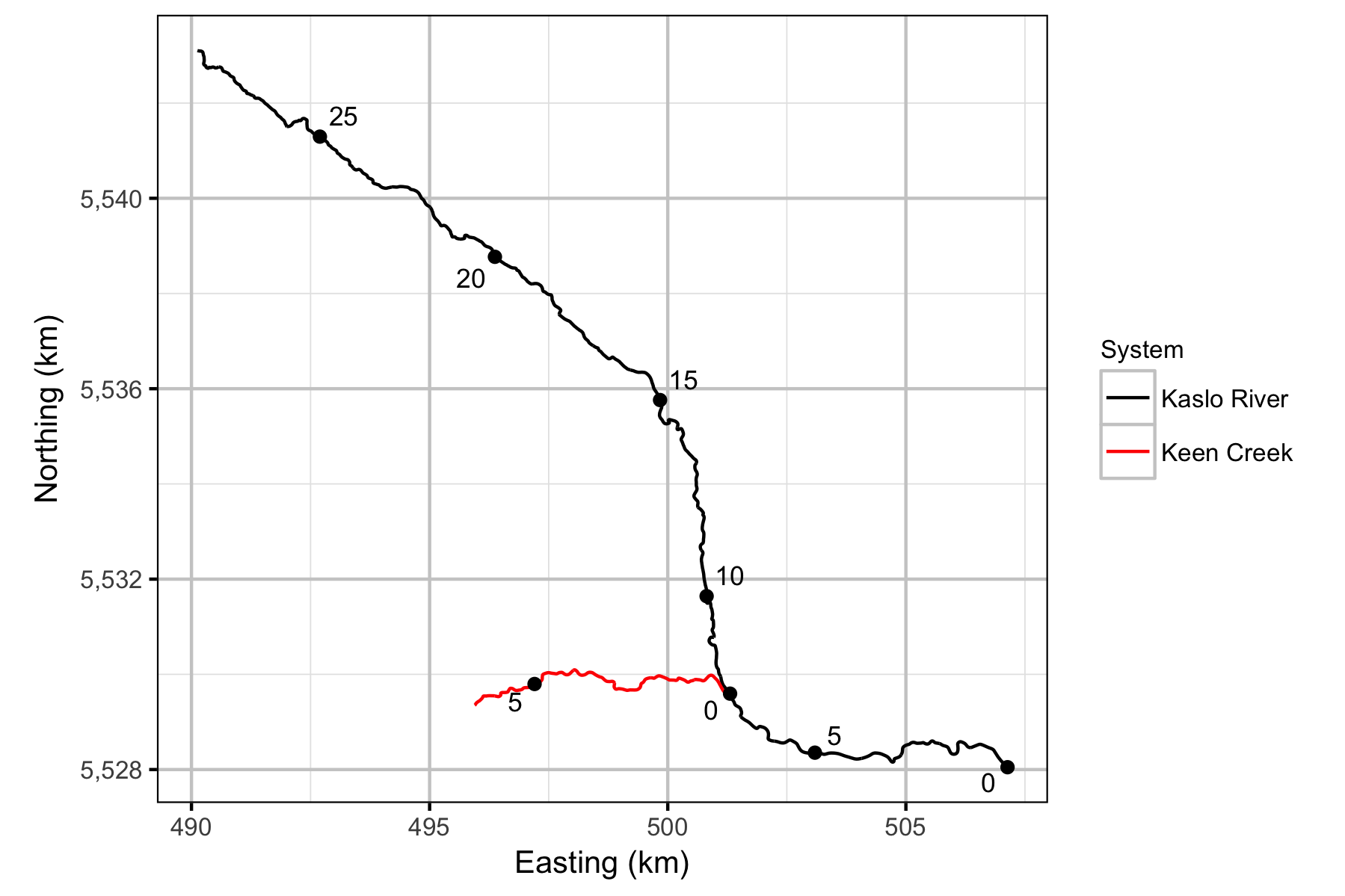
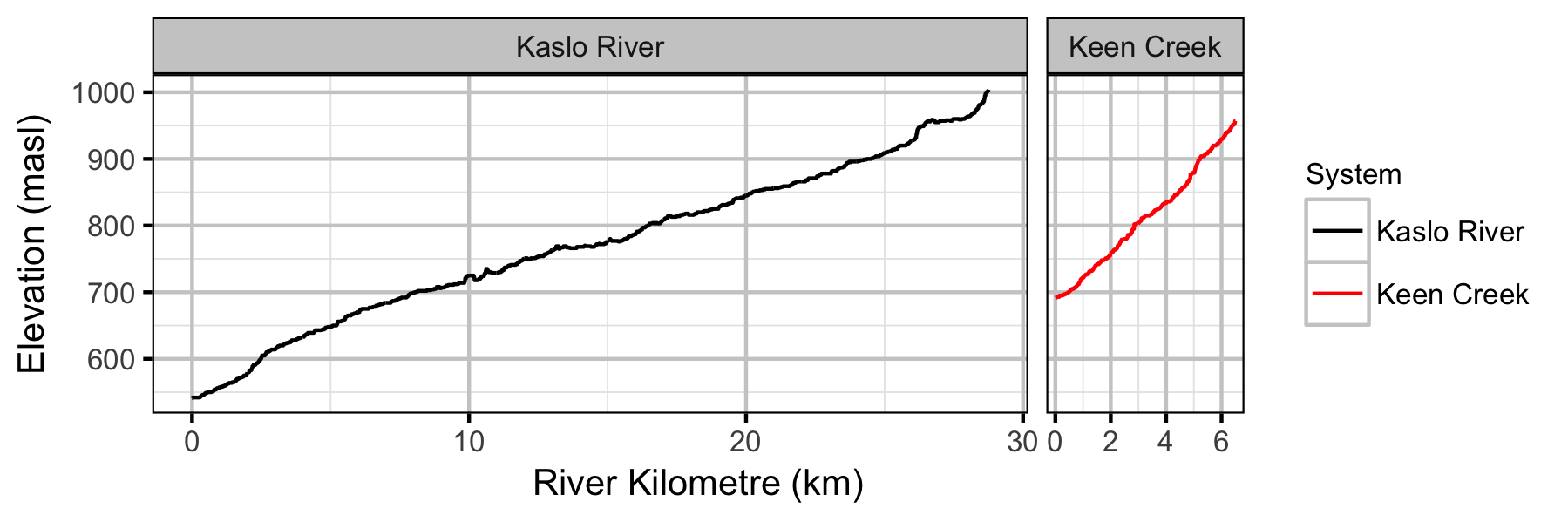
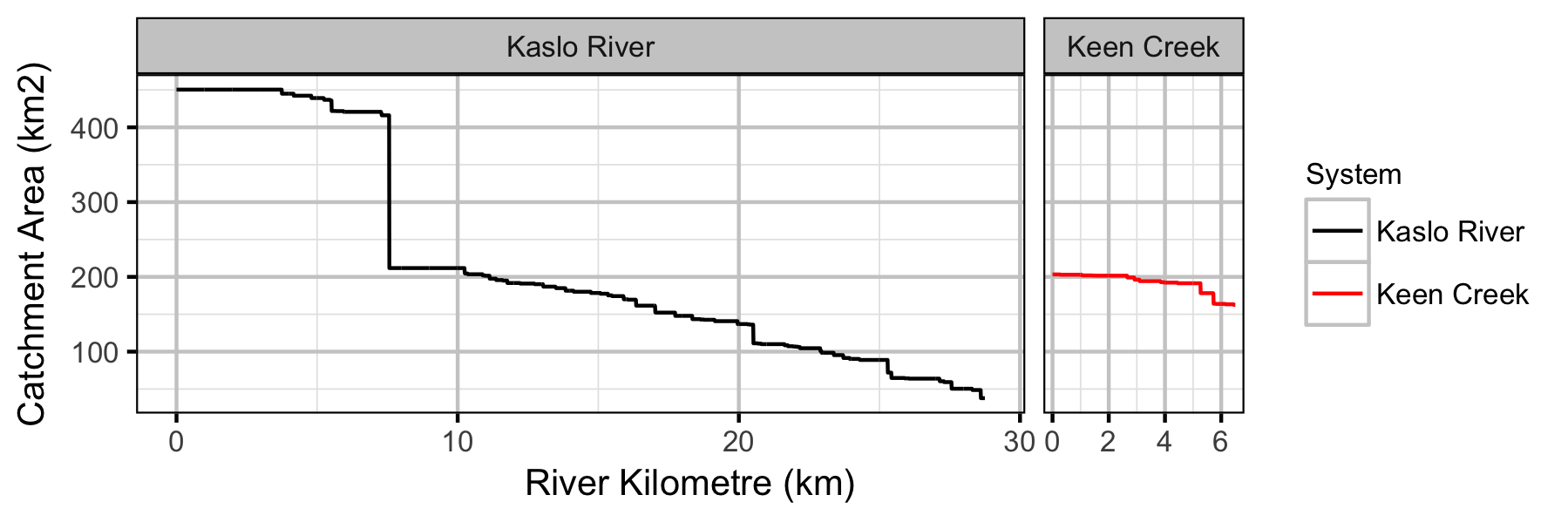
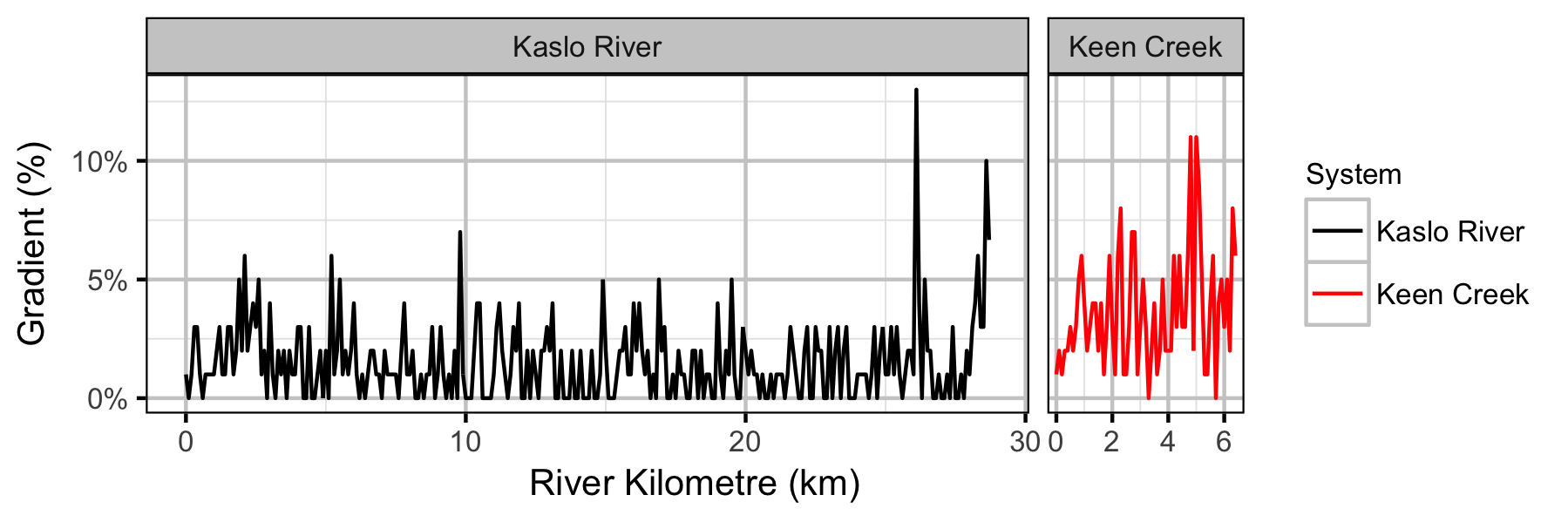
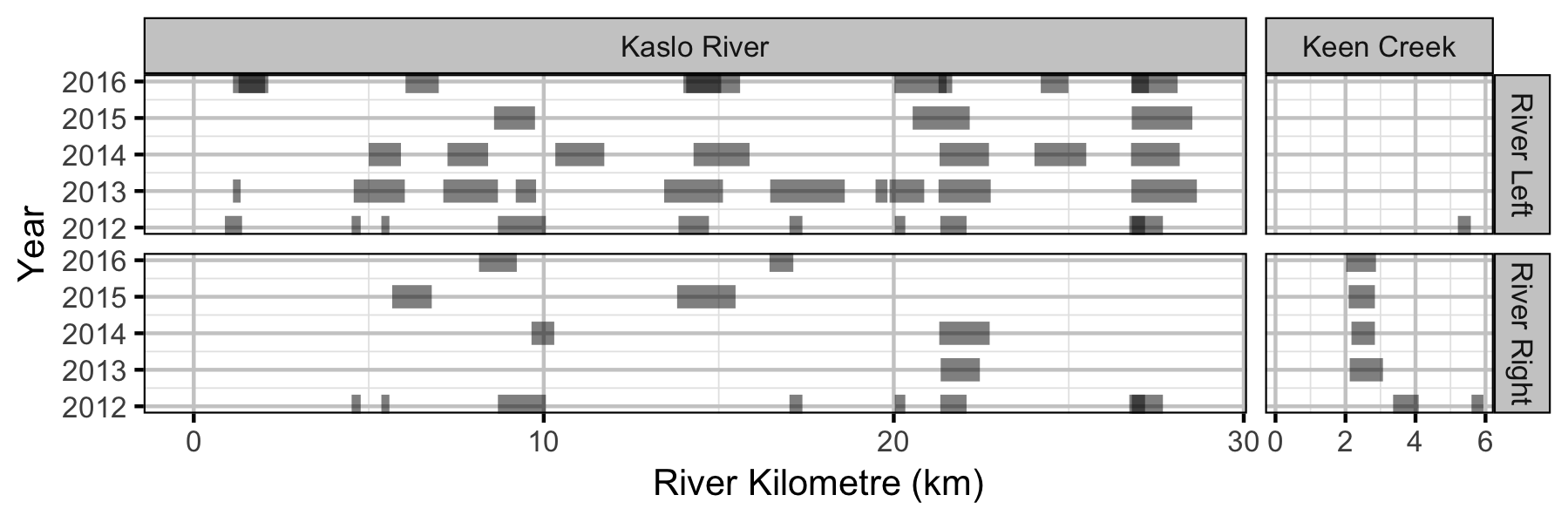
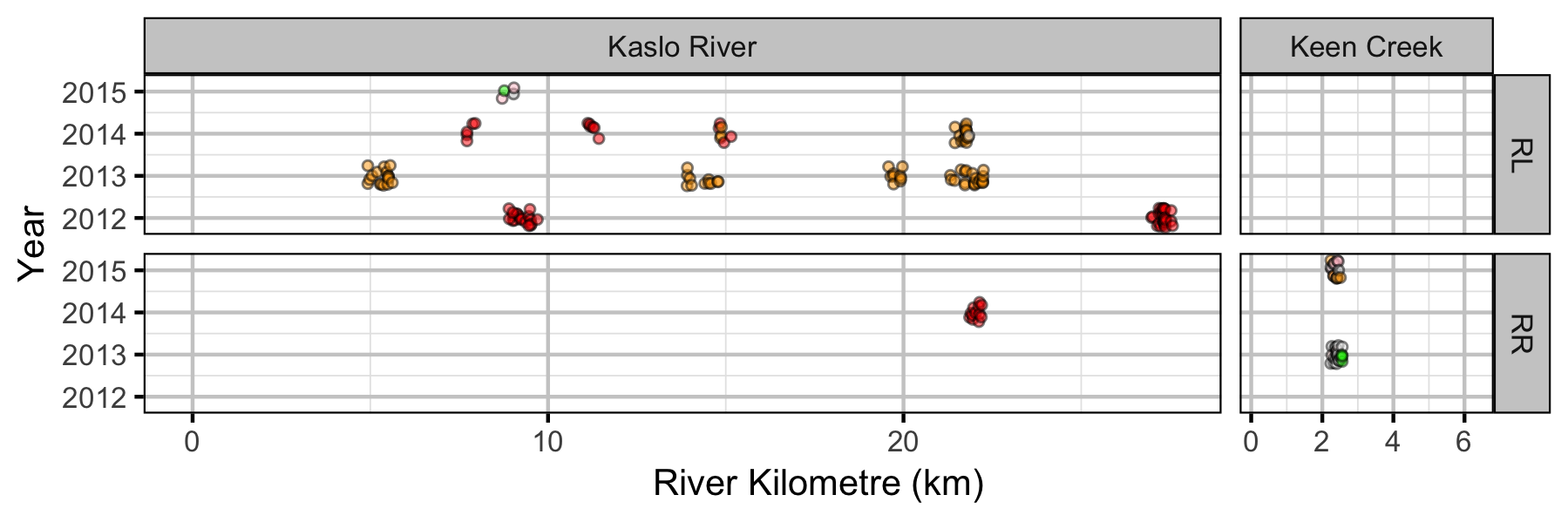
Sites
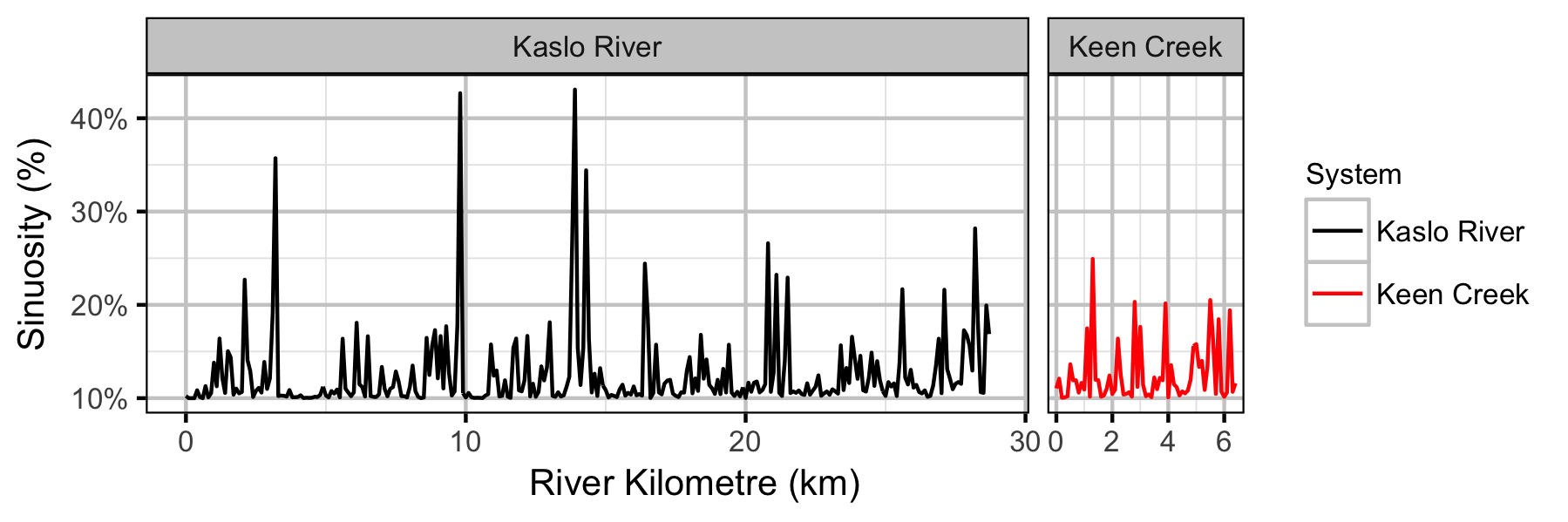
Coverage
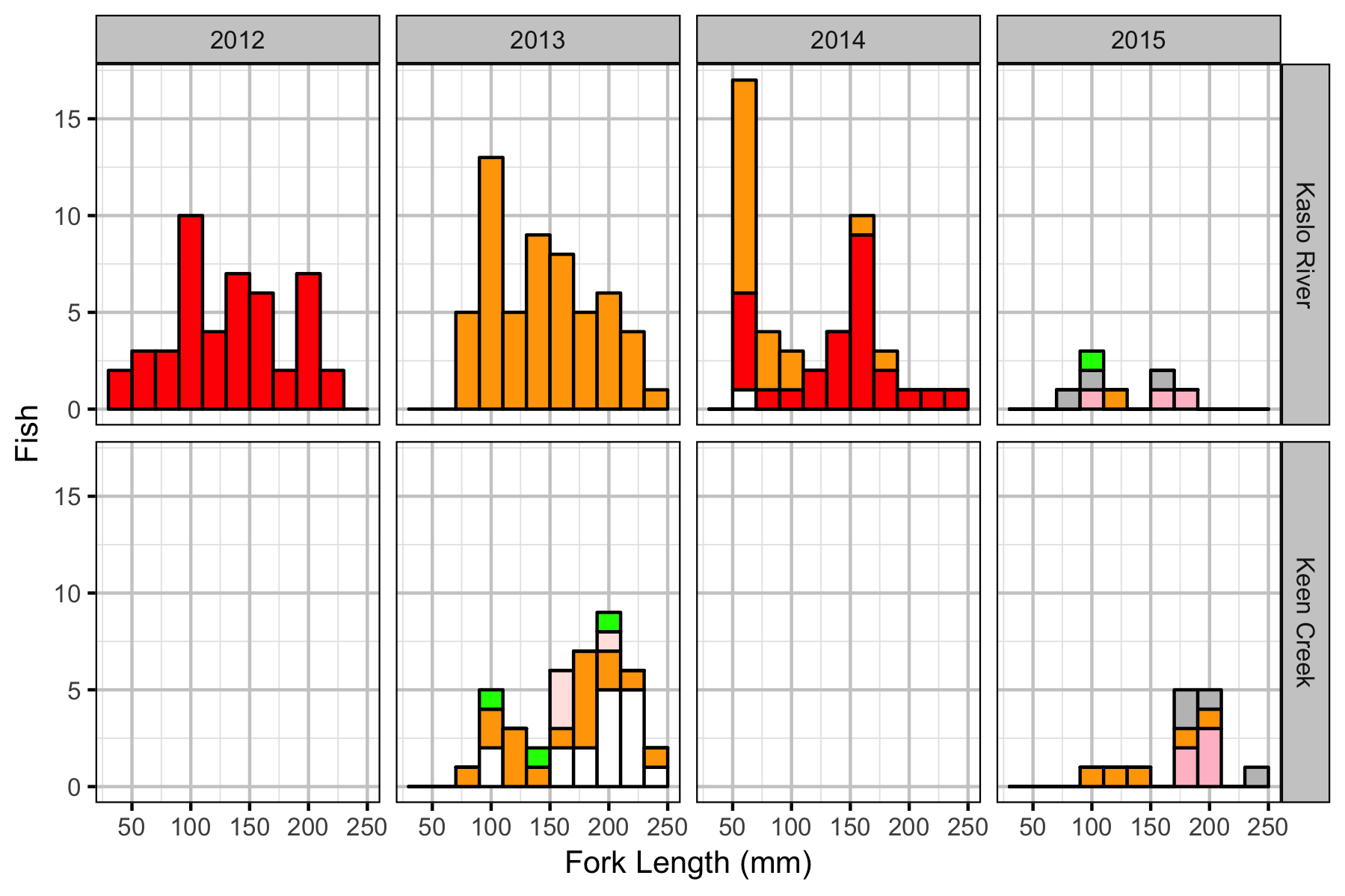
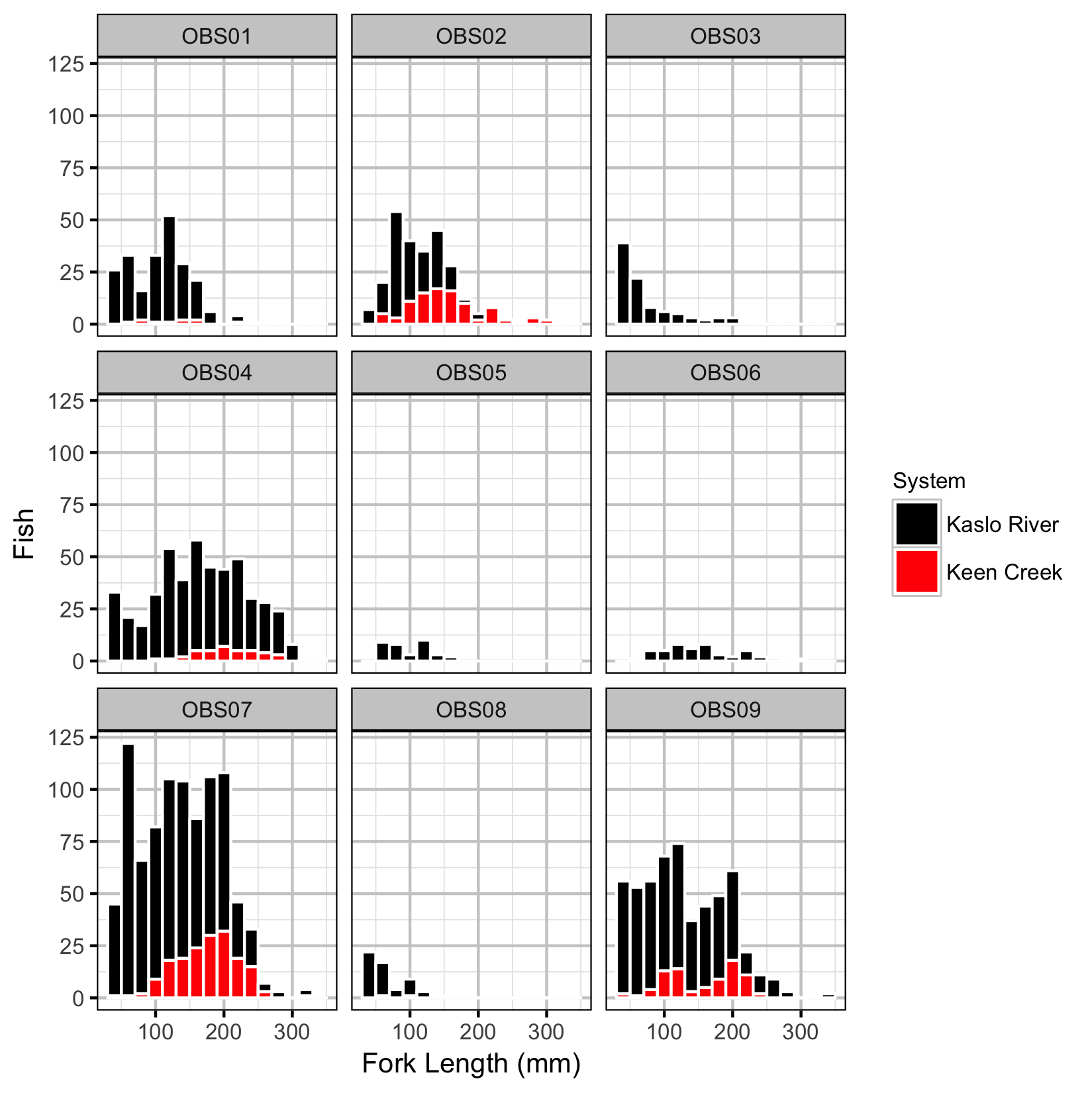
Fish
Observer Efficiency
Bayesian
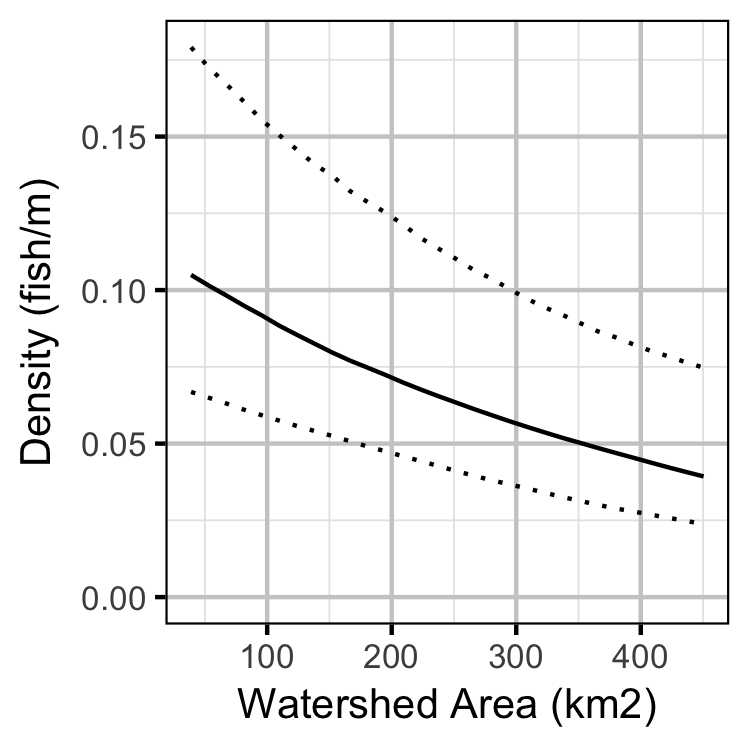
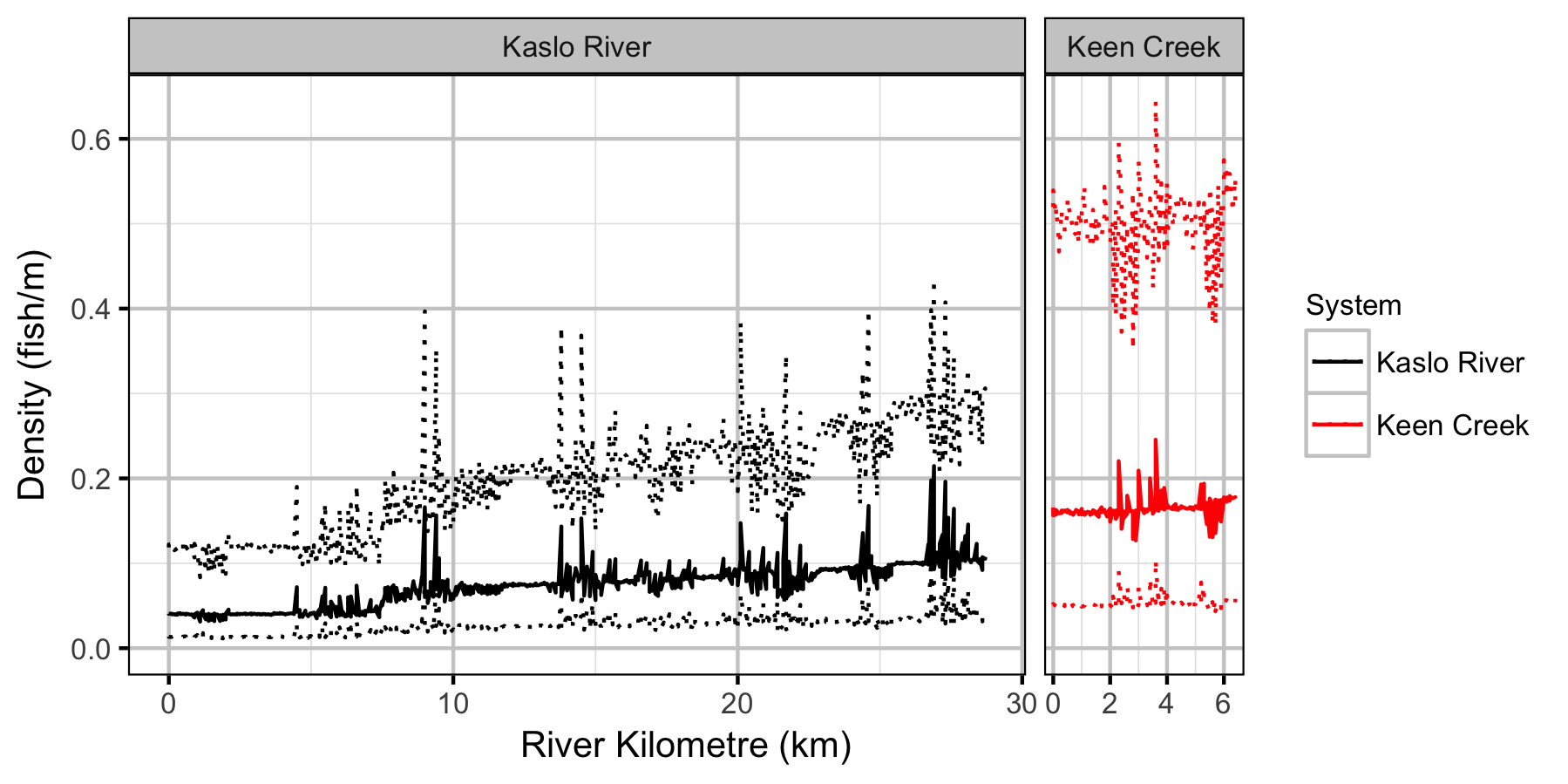
Lineal Density
Bayesian
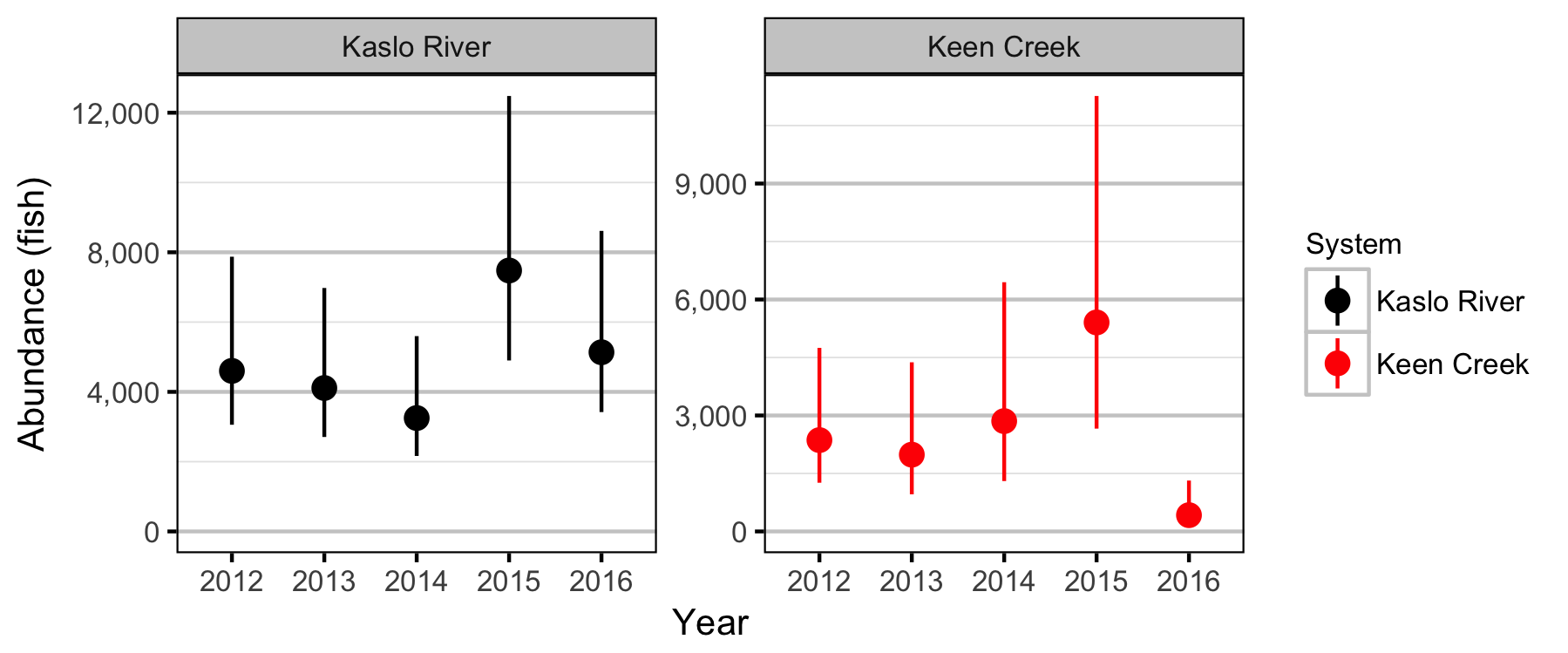
Stock-Recruiment
Bayesian
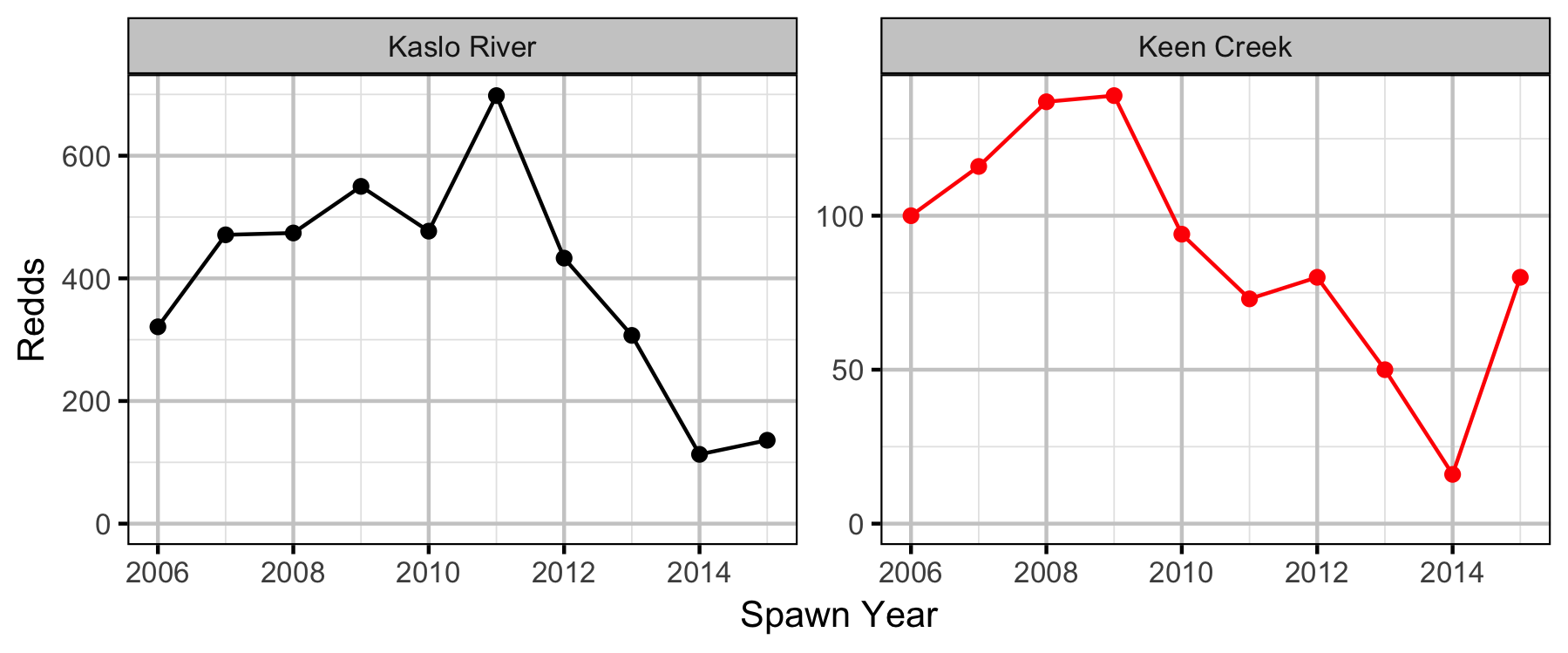
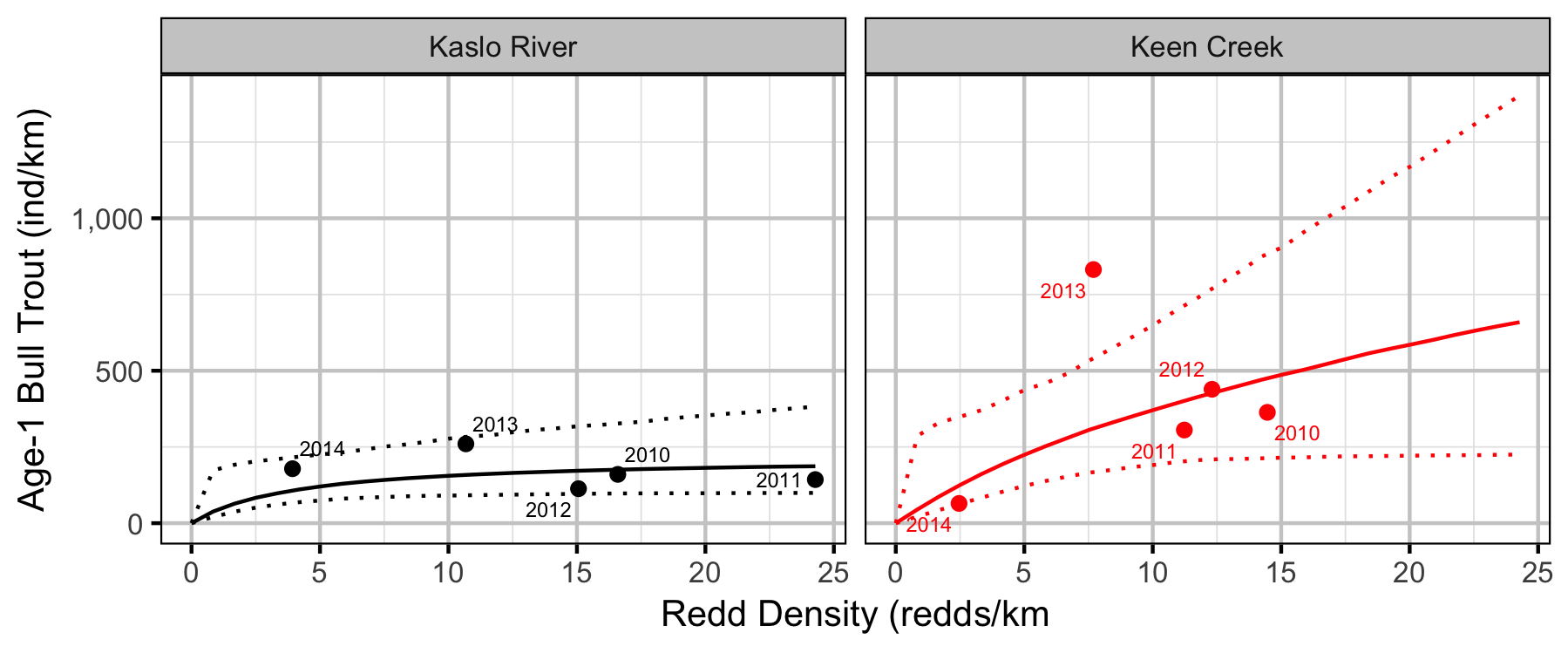
Conclusions
- Observer efficiency is very low for age-0 Bull Trout and increases with size.
- Sinuosity and gradient are not important predictors of the densities of age-1 Bull Trout in Keen Creek and the Kaslo River.
Recommendations
- Field
- Vary tag colors by fish lengths and locations so it is easy to match resighted fish to individual tagged fish.
- GIS
- Map river locations to the 1 m scale.
- Analytic
- Quantify observer differences in length estimation and efficiency.
- Model autocorrelation in site densities.
- Compare explanatory power of river kilometre versus watershed area.
Acknowledgements
The organisations and individuals whose contributions have made this analysis report possible include:
- BC Fish and Wildlife
- Greg Andrusak
- Gary Pavan
- Stephan Himmer
- Jimmy Robbins
- Gillian Sanders
- Jason Bowers
- Jeff Berdusco
- Kyle Mace
References
Bradford, Michael J, Josh Korman, and Paul S Higgins. 2005. “Using Confidence Intervals to Estimate the Response of Salmon Populations (Oncorhynchus Spp.) to Experimental Habitat Alterations.” Canadian Journal of Fisheries and Aquatic Sciences 62 (12): 2716–26. https://doi.org/10.1139/f05-179.
Burnham, Kenneth P., and David R. Anderson. 2002. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Vol. Second Edition. New York: Springer.
Kery, Marc, and Michael Schaub. 2011. Bayesian Population Analysis Using WinBUGS : A Hierarchical Perspective. Boston: Academic Press. http://www.vogelwarte.ch/bpa.html.
Kristensen, Kasper, Anders Nielsen, Casper W. Berg, Hans Skaug, and Bradley M. Bell. 2016. “TMB : Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software 70 (5). https://doi.org/10.18637/jss.v070.i05.
Millar, R. B. 2011. Maximum Likelihood Estimation and Inference: With Examples in R, SAS, and ADMB. Statistics in Practice. Chichester, West Sussex: Wiley.
Plummer, Martyn. 2015. “JAGS Version 4.0.1 User Manual.” http://sourceforge.net/projects/mcmc-jags/files/Manuals/4.x/.
R Core Team. 2015. “R: A Language and Environment for Statistical Computing.” Vienna, Austria: R Foundation for Statistical Computing. http://www.R-project.org/.