Horse Lake Exploitation Analysis 2019
The suggested citation for this analytic report is:
Dalgarno, S. and Thorley, J.L. (2019) Horse Lake Exploitation Analysis 2019. A Poisson Consulting Analytic Appendix. URL: https://www.poissonconsulting.ca/f/248424047.
Background
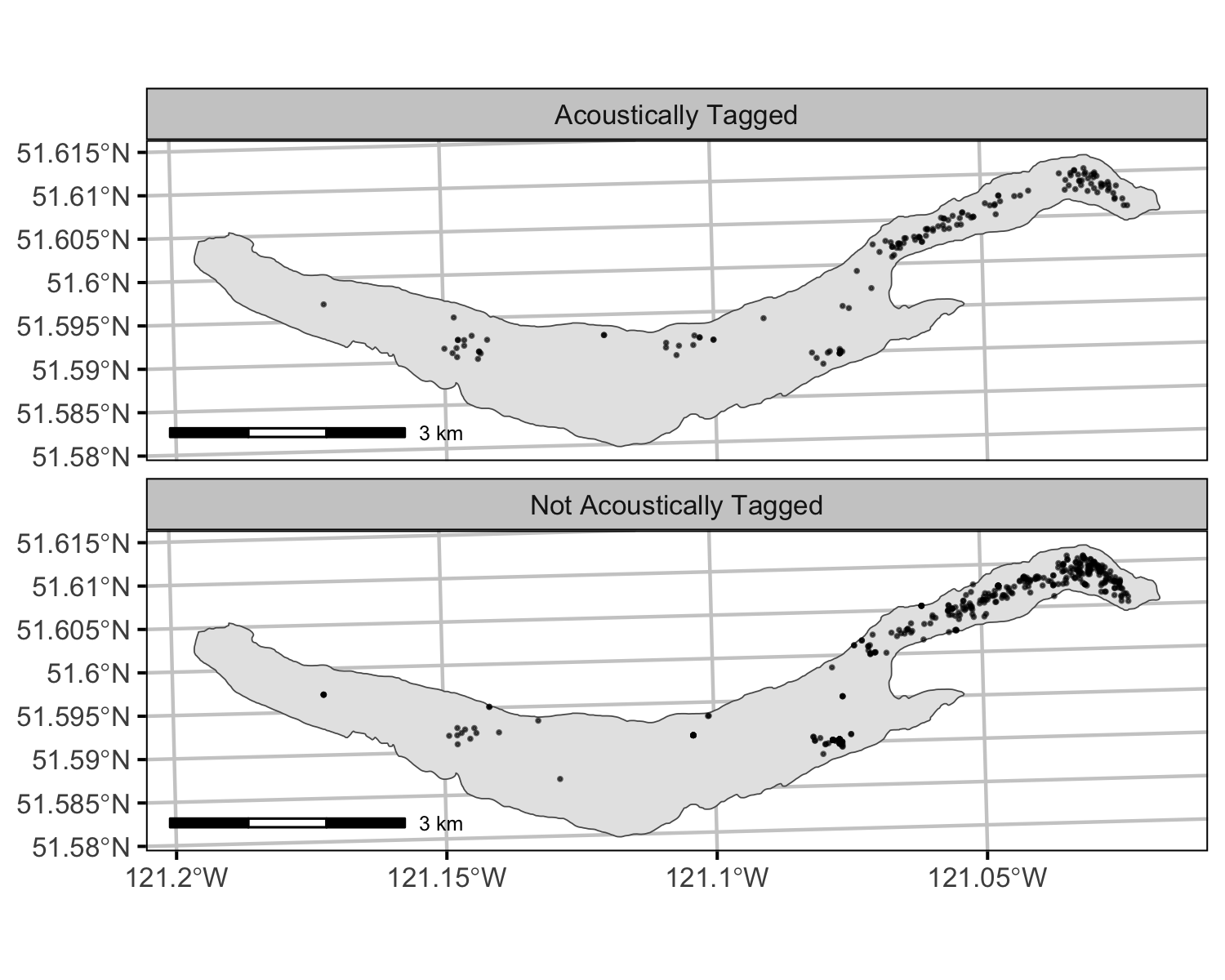
Horse Lake supports a recreational fishery for Lake Trout (Salvelinus namaycush). To estimate their natural and fishing mortality, individuals were caught by angling and tagged with acoustic transmitters and/or external reward tags. Acoustically tagged fish were detected by a series of seven receivers distributed through the lake as well as annual mobile receiver surveys. The external reward tags included a phone number for anglers to report their recaptures. In 2019, eight Rainbow Trout with acoustic transmitters and external reward tags were transplanted from Greenlee Lake.
All the data were provided by the Ministry of Forests, Lands and Natural Resource Operations (MFLNRO) Cariboo Region.
Methods
Data Preparation
The data were prepared for analysis using R version 3.6.1 (R Core Team 2019). Receivers were assumed to have a detection range of 500 m. Detections were aggregated daily, where for each transmitter the receiver with the most detections was chosen. In the case of a tie, the receiver with the greatest coverage area was chosen.
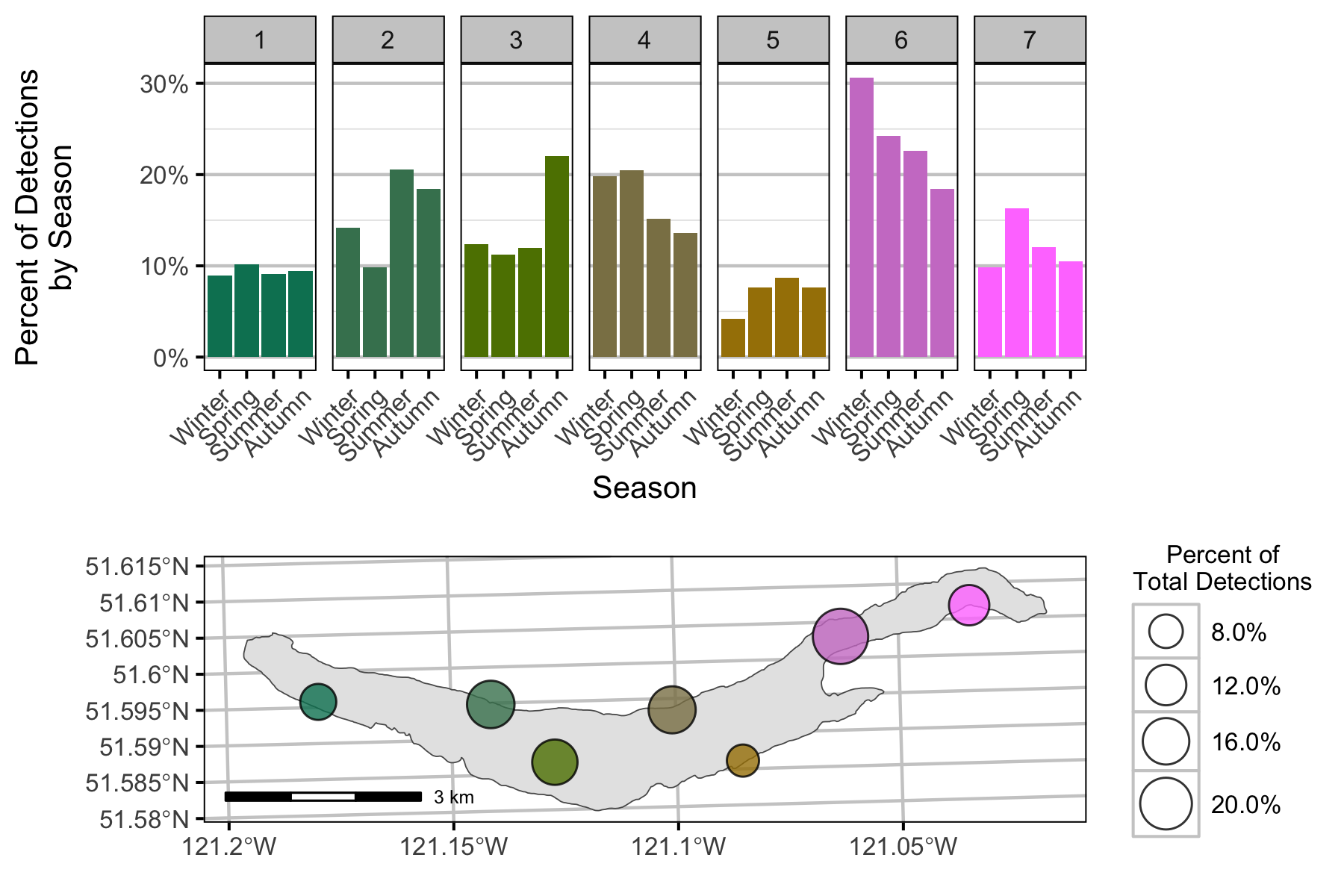
The Seasons were Winter (December - February), Spring (March - May), Summer (June - August) and Autumn (September - November).
Data Analysis
Hierarchical Bayesian models were fitted to the data using R version
3.6.1 (R Core Team 2019) and JAGS 4.2.0 (Plummer 2015) which
interfaced with each other via the jmbr package. For additional
information on hierarchical Bayesian modelling in the BUGS language, of
which JAGS uses a dialect, the reader is referred to Kery and Schaub (2011, 41–44).
Unless indicated otherwise, the Bayesian analyses used normal and half-normal prior distributions that were vague in the sense that they did not constrain the posteriors (Kery and Schaub 2011, 36). The posterior distributions were estimated from 1500 Markov Chain Monte Carlo (MCMC) samples thinned from the second halves of 3 chains (Kery and Schaub 2011, 38–40). Model convergence was confirmed by ensuring that \(\hat{R} \leq 1.05\) (Kery and Schaub 2011, 40) and \(\textrm{ESS} \geq 150\) for each of the monitored parameters (Kery and Schaub 2011, 61). Where \(\hat{R}\) is the potential scale reduction factor and \(\textrm{ESS}\) is the effective sample size (Brooks et al. 2011).
The posterior distributions of the fixed (Kery and Schaub 2011, 75) parameters are summarised in terms of the point estimate, standard deviation (sd), the z-score, lower and upper 95% confidence/credible limits (CLs) and the p-value (Kery and Schaub 2011, 37, 42). The estimate is the median (50th percentile) of the MCMC samples, the z-score is \(\mathrm{sd}/\mathrm{mean}\) and the 95% CLs are the 2.5th and 97.5th percentiles. A p-value of 0.05 indicates that the lower or upper 95% CL is 0.
The results are displayed graphically by plotting the modeled relationships between particular variables and the response with the remaining variables held constant. In general, continuous and discrete fixed variables are held constant at their mean and first level values respectively while random variables are held constant at their typical values (expected values of the underlying hyperdistributions) (Kery and Schaub 2011, 77–82). Where informative the influence of particular variables is expressed in terms of the effect size (i.e., percent change in the response variable) with 95% CIs (Bradford, Korman, and Higgins 2005).
Model Descriptions
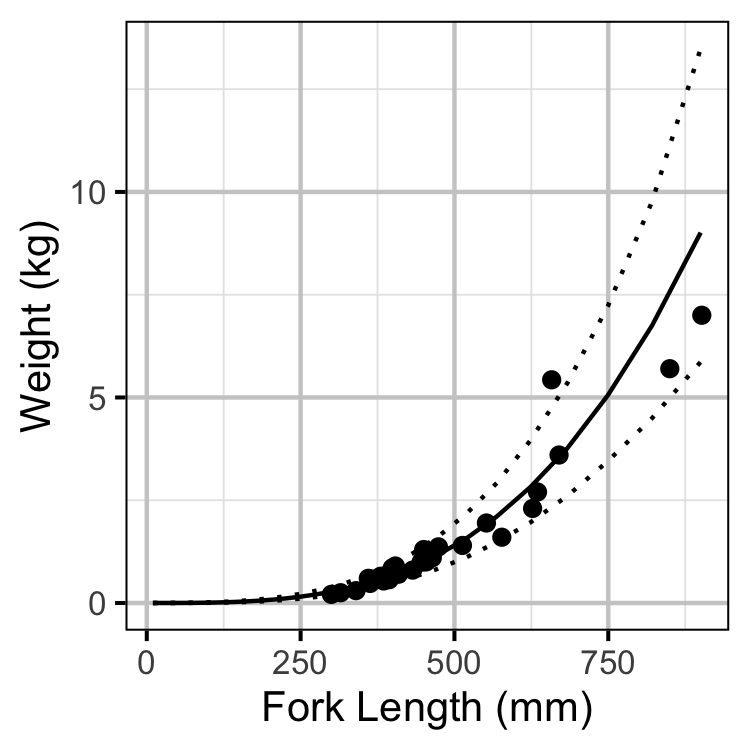
Condition
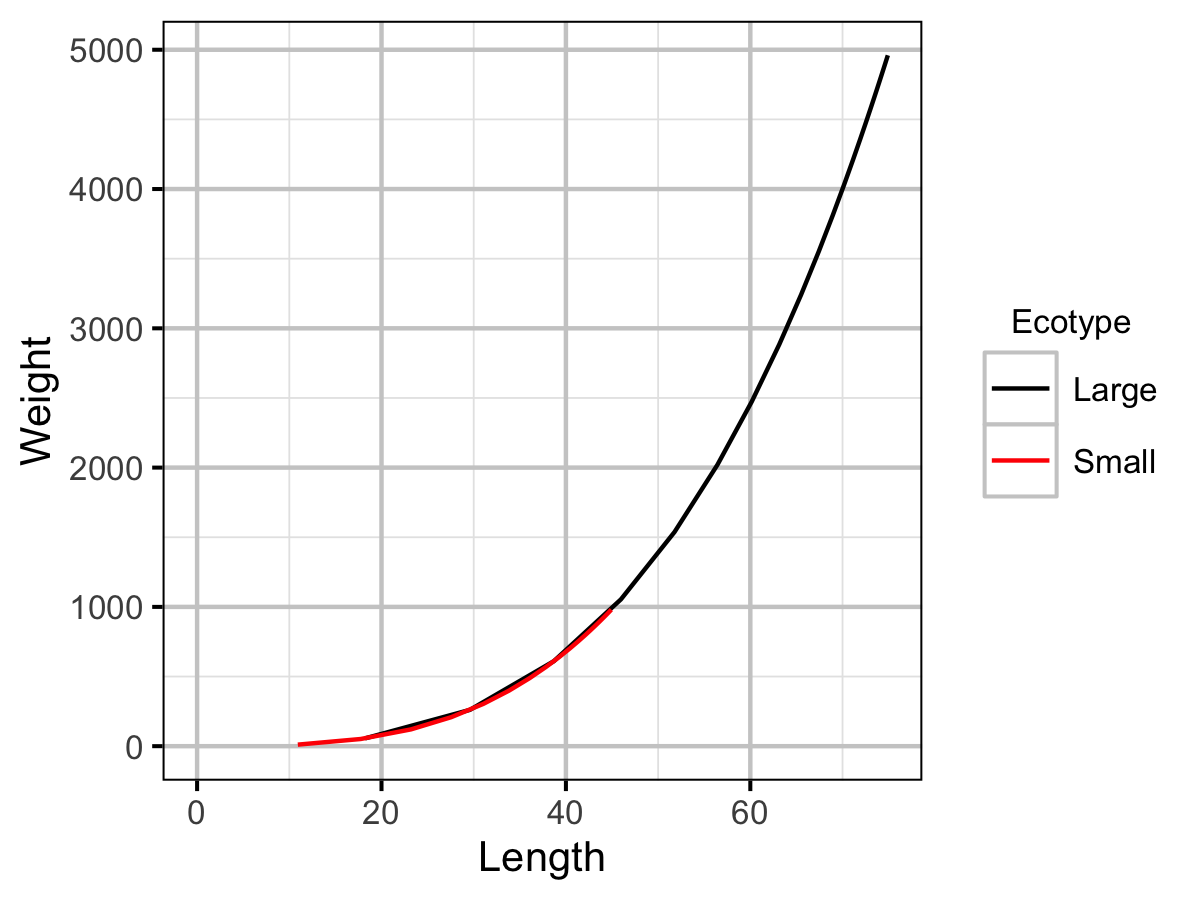
The expected weight of a fish of a given length was estimated from the data using a allometric mass-length model (He et al. 2008)
\[ L = \alpha W^\beta\]
Key assumptions of the condition model include:
- The prior distribution on the power term (\(\beta\)) is a normal distribution with a mean of 3.18 and a standard deviation of 0.19 (McDermid, Shuter, and Lester 2010).
- The residual variation in weight is log-normally distributed.
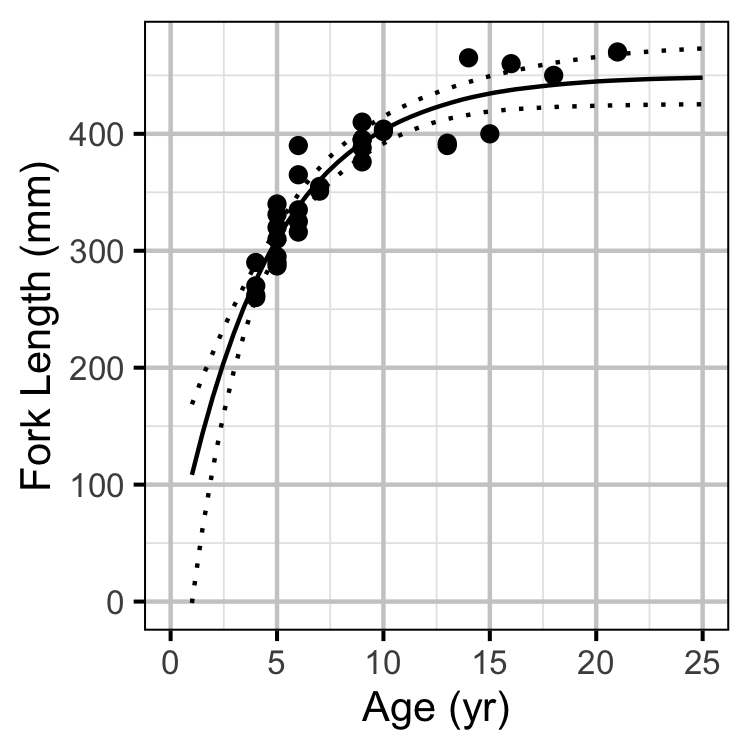
Growth
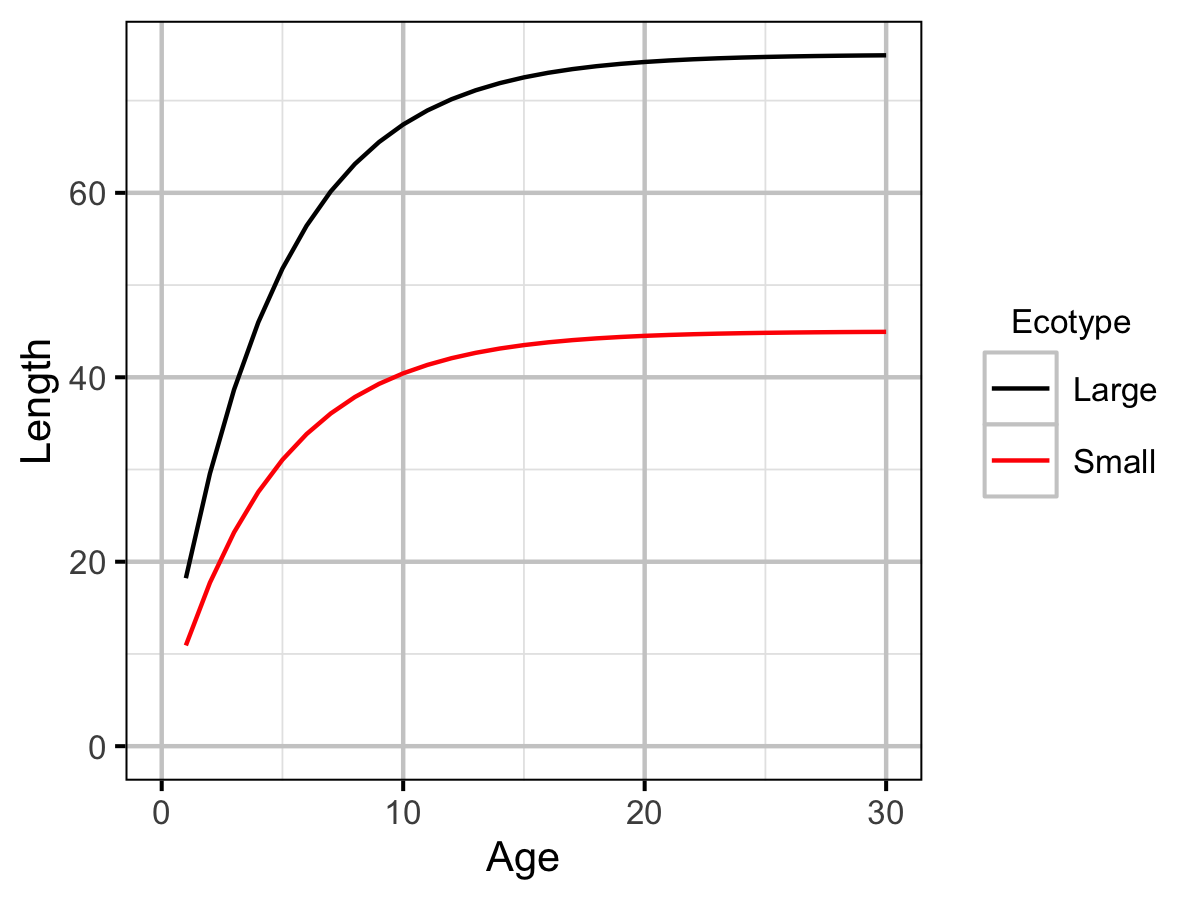
Growth was estimated from length and scale age data for Horse Lake using a Von Bertalanffy growth curve model (von Bertalanffy 1938).
\[ L = L_\infty \cdot (1 - \exp(-k \cdot (A - t_0) ))\]
where \(A\) is the scale age in years and \(t_0\) is the extrapolated age at zero length.
Key assumptions of the growth model include:
- The residual variation in length is normally distributed.
1 fish with a fork length \(\geq\) 500 mm was excluded from the analysis.
Survival
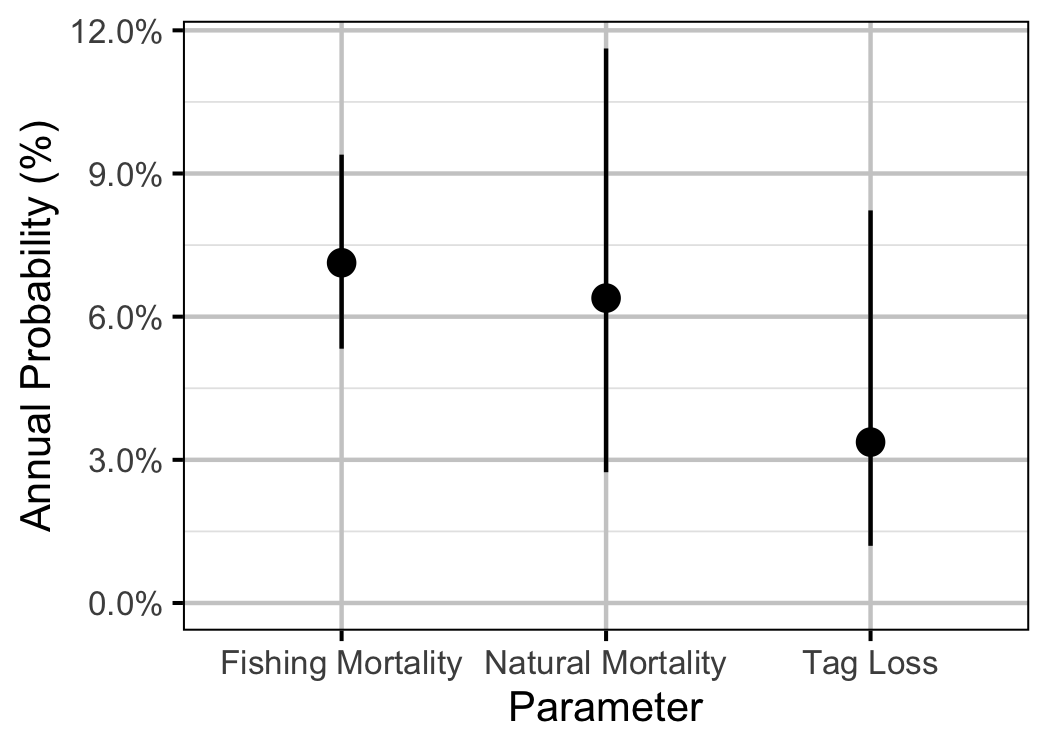
The natural mortality and capture probability for individuals \(\geq\) 300 mm was estimated using a Bayesian individual state-space survival model (Thorley and Andrusak 2017) with monthly intervals. The survival model incorporated natural and handling mortality, acoustic detection, movement, T-bar tag loss, recapture and reporting. Key assumptions of the survival model include:
- The tagged individuals are a random sample from the population.
- The only effects of tagging are change in the natural mortality for three months following acoustic tagging.
- The prior probability on the annual interval individual external tag loss rate is a uniform distribution between 1 and 30% (Fabrizio et al. 1996).
- All individuals are correctly identified.
- There is no emigration out of the lake.
- There are no unmodelled individual differences in the probability of recapture in each time interval.
- There are no unmodelled individual differences in the probability of survival in each time interval.
- There are no unmodelled individual differences in the probability of a living individual with an active acoustic transmitter being detected moving among sections in each time period.
- The fate of each individual is independent of the fate of any other individual.
- The sampling periods are instantaneous and all individuals are immediately released.
The survival model treats all recaptured fish as if they had been retained. Only individuals with a fork length (FL) \(\geq\) 300 mm that were tagged with an acoustic tag and/or $100 and $10 reward tags were included in the survival analysis. Preliminary analysis indicated that the difference between the natural mortality and fishing mortality rates for individuals \(\geq\) 500 mm were not sigificant.
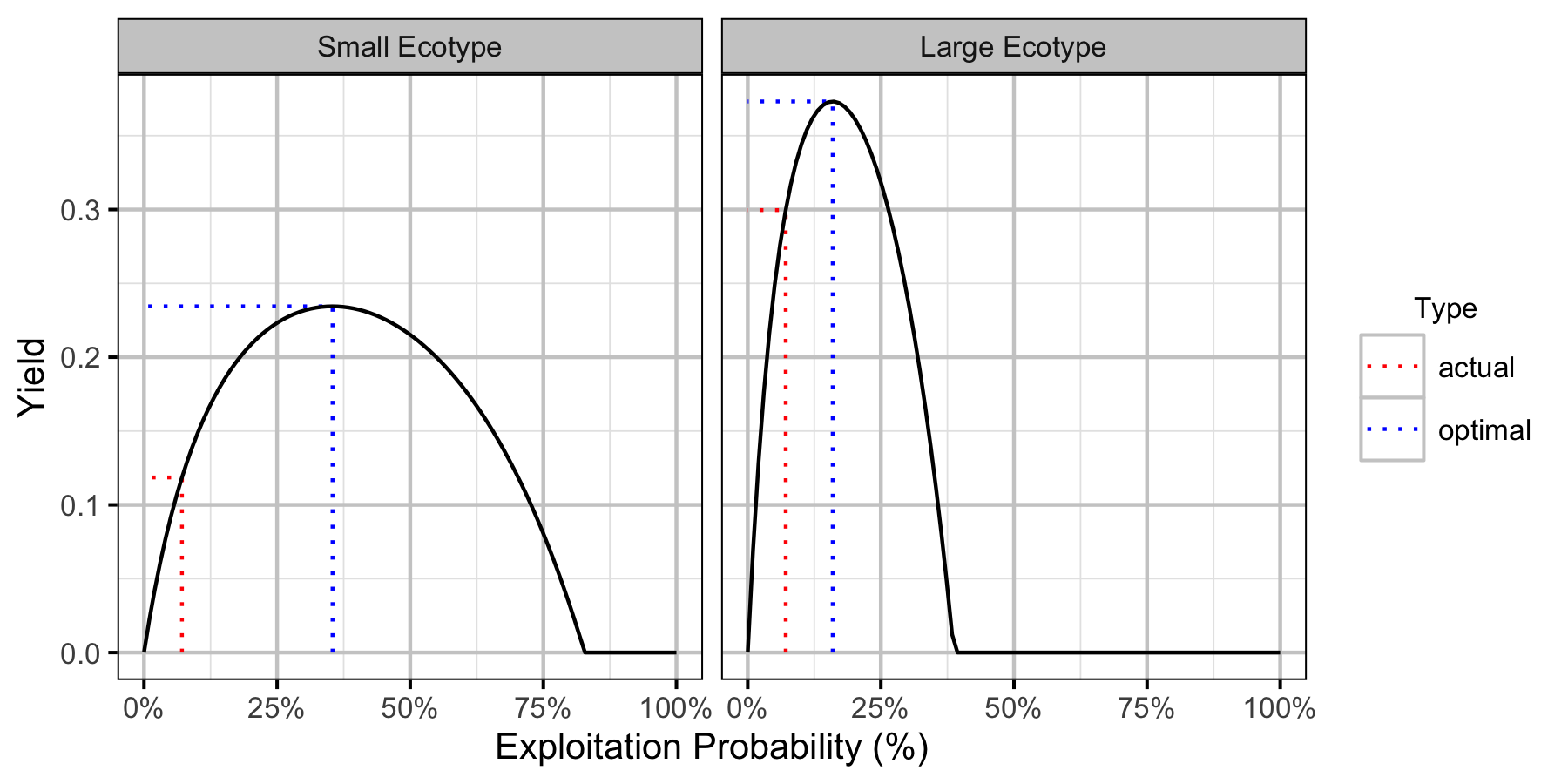
Yield-Per-Recruit
The optimal capture rate (to maximize number of individuals harvested assuming 100% retention) was calculated using yield-per-recruit analysis (Walters and Martell 2004). A separate yield-per-recruit analysis was performed for the two different Lake Trout ecotypes in Horse Lake.
Results
Templates
Condition
.model {
bWeight ~ dnorm(0, 1^-2)
bWeightLength ~ dnorm(3.18, 0.19^-2)
sWeight ~ dnorm(0, 1^-2) T(0,)
for(i in 1:length(LogLength)) {
eWeight[i] <- bWeight + bWeightLength * LogLength[i]
Weight[i] ~ dlnorm(eWeight[i], exp(sWeight)^-2)
}
..Block 1. Condition model description.
Growth
.model {
bLInf ~ dnorm(500, 100^-2) T(0, )
bK ~ dnorm(0, 1^-2) T(0, )
bT0 ~ dnorm(0, 1^-1)
sLength ~ dnorm(0, 100^-2) T(0, )
for (i in 1:length(Length)) {
eLength[i] <- bLInf * (1 - exp(-bK * (Age[i] - bT0)))
Length[i] ~ dnorm(eLength[i], sLength^-2) T(0, )
}
..Block 2. Growth model description.
Survival
.model{
bMortality ~ dnorm(-3, 3^-2)
bMortalityHandling ~ dnorm(0, 2^-2)
bTagLoss ~ dunif(1 - (1 - 0.01)^(1/12), 1 - (1 - 0.30)^(1/12))
bDetected ~ dunif(0, 1)
bMoved ~ dunif(0, 1)
bRecaptured ~ dunif(0, 1 - (1 - 0.50)^(1/12))
bReported ~ dunif(0.9, 1.00)
for (i in 1:nCapture){
logit(eMortality[i,PeriodCapture[i]]) <- bMortality + bMortalityHandling
eTagLoss[i,PeriodCapture[i]] <- bTagLoss
eDetected[i,PeriodCapture[i]] <- bDetected
eMoved[i,PeriodCapture[i]] <- bMoved
eRecaptured[i,PeriodCapture[i]] <- bRecaptured
eReported[i,PeriodCapture[i]] <- bReported
InLake[i,PeriodCapture[i]] <- 1
Alive[i,PeriodCapture[i]] ~ dbern(1-eMortality[i,PeriodCapture[i]])
TBarTag100[i,PeriodCapture[i]] ~ dbern(1-eTagLoss[i,PeriodCapture[i]])
TBarTag10[i,PeriodCapture[i]] ~ dbern(1-eTagLoss[i,PeriodCapture[i]])
Detected[i,PeriodCapture[i]] ~ dbern(Monitored[i,PeriodCapture[i]] * eDetected[i,PeriodCapture[i]])
Moved[i,PeriodCapture[i]] ~ dbern(Alive[i,PeriodCapture[i]] * Monitored[i,PeriodCapture[i]] * eMoved[i,PeriodCapture[i]])
Recaptured[i,PeriodCapture[i]] ~ dbern(Alive[i,PeriodCapture[i]] * eRecaptured[i,PeriodCapture[i]])
Reported[i,PeriodCapture[i]] ~ dbern(Recaptured[i,PeriodCapture[i]] * eReported[i,PeriodCapture[i]] * step(TBarTag100[i,PeriodCapture[i]] + TBarTag10[i,PeriodCapture[i]] - 1))
for(j in (PeriodCapture[i]+1):nPeriod) {
logit(eMortality[i,j]) <- bMortality + bMortalityHandling * step(PeriodCapture[i] - j + 2)
eTagLoss[i,j] <- bTagLoss
eDetected[i,j] <- bDetected
eMoved[i,j] <- bMoved
eRecaptured[i,j] <- bRecaptured
eReported[i,j] <- bReported
InLake[i,j] ~ dbern(InLake[i,j-1] * (1-Recaptured[i,j-1]))
Alive[i,j] ~ dbern(Alive[i,j-1] * (1-Recaptured[i,j-1]) * (1-eMortality[i,j-1]))
TBarTag100[i,j] ~ dbern(TBarTag100[i,j-1] * (1-Recaptured[i,j-1]) * (1-eTagLoss[i,j]))
TBarTag10[i,j] ~ dbern(TBarTag10[i,j-1] * (1-Recaptured[i,j-1]) * (1-eTagLoss[i,j]))
Detected[i,j] ~ dbern(InLake[i,j] * Monitored[i,j] * eDetected[i,j])
Moved[i,j] ~ dbern(Alive[i,j] * Monitored[i,j] * eMoved[i,j])
Recaptured[i,j] ~ dbern(Alive[i,j] * eRecaptured[i,j])
Reported[i,j] ~ dbern(Recaptured[i,j] * eReported[i,j] * step(TBarTag100[i,j] + TBarTag10[i,j] - 1))}}
}Block 3. Survival model description.
Tables
Captures
Table 1. Number of fish captured by year, species and size class. Eight Rainbow Trout were transplanted in 2019.
| Year | Species | < 300 mm | 300 - 500 mm | >= 500 mm | Total |
|---|---|---|---|---|---|
| 2017 | Kokanee | 3 | 20 | 0 | 23 |
| 2017 | Lake Trout | 1 | 153 | 7 | 161 |
| 2017 | Rainbow Trout | 0 | 3 | 0 | 3 |
| 2018 | Kokanee | 0 | 2 | 0 | 2 |
| 2018 | Lake Trout | 4 | 176 | 19 | 199 |
| 2019 | Lake Trout | 3 | 154 | 7 | 164 |
| 2019 | Rainbow Trout | 0 | 8 | 0 | 8 |
| Total | 11 | 516 | 33 | 560 |
Table 2. Number of Lake Trout captured by size class, and tag class. Any fish > 500mm is classified as ‘large’.
| Year | Size | Acoustic and T-Bar | T-Bar Only | No Tag | Total |
|---|---|---|---|---|---|
| 2017 | < 300 mm | 0 | 1 | 0 | 1 |
| 2017 | 300 - 500 mm | 29 | 113 | 11 | 153 |
| 2017 | >= 500 mm | 3 | 2 | 2 | 7 |
| 2018 | < 300 mm | 0 | 2 | 2 | 4 |
| 2018 | 300 - 500 mm | 43 | 103 | 30 | 176 |
| 2018 | >= 500 mm | 11 | 4 | 4 | 19 |
| 2019 | < 300 mm | 0 | 3 | 0 | 3 |
| 2019 | 300 - 500 mm | 56 | 98 | 0 | 154 |
| 2019 | >= 500 mm | 4 | 3 | 0 | 7 |
| Total | 146 | 329 | 49 | 524 |
Recaptures
Table 3. All Lake Trout recaptures to date. Recaptures with natural mortality were tags found in the stomach of another fish!.
| Date Capture | Fork Length (mm) | Date Recapture | External Tag Number 1 | External Tag Number 2 | Harvested | Natural Mortality |
|---|---|---|---|---|---|---|
| 2017-06-06 | 445 [mm] 20 | 17-07-07 | 278 | 544 Ye | s No | |
| 2017-05-20 | 405 [mm] 20 | 17-09-08 | 86 | 337 Ye | s No | |
| 2017-06-01 | 441 [mm] 20 | 18-01-29 | 289 | 532 Ye | s No | |
| 2017-05-31 | 385 [mm] 20 | 18-02-02 | 441 | NA Ye | s No | |
| 2017-06-07 | 439 [mm] 20 | 18-02-08 | 413 | 258 Ye | s No | |
| 2018-05-25 | 400 [mm] 20 | 18-05-28 | 1390 | 2315 Ye | s No | |
| 2017-05-18 | 360 [mm] 20 | 18-05-29 | 326 | 76 No | No | |
| 2018-05-29 | 379 [mm] 20 | 18-05-29 | 151 | 445 No | No | |
| 2017-05-31 | 357 [mm] 20 | 18-05-29 | 151 | 445 No | No | |
| 2018-05-25 | 436 [mm] 20 | 18-06-28 | 1391 | 2316 Ye | s No | |
| 2018-05-30 | 341 [mm] 20 | 18-07-03 | 2370 | NA Ye | s Ye | s |
| 2018-06-11 | 406 [mm] 20 | 18-07-03 | 136 | 552 Ye | s Ye | s |
| 2017-05-21 | 370 [mm] 20 | 18-07-05 | 340 | 89 Ye | s No | |
| 2017-06-07 | 416 [mm] 20 | 18-07-16 | 404 | 251 Ye | s No | |
| 2018-05-25 | 334 [mm] 20 | 18-07-18 | 2320 | 1395 Ye | s No | |
| 2018-05-30 | 416 [mm] 20 | 18-07-24 | 2368 | 1335 No | No | |
| 2017-06-02 | 360 [mm] 20 | 18-09-10 | 538 | NA No | No | |
| 2018-05-31 | 411 [mm] 20 | 19-01-15 | 2386 | 362 Ye | s No | |
| 2018-06-08 | 382 [mm] 20 | 19-01-25 | 2340 | 377 Ye | s No | |
| 2017-05-18 | 360 [mm] 20 | 19-03-09 | 76 | 326 Ye | s No | |
| 2018-06-07 | 325 [mm] 20 | 19-03-09 | 2327 | 390 Ye | s No | |
| 2017-05-30 | 402 [mm] 20 | 19-03-31 | 56 | 512 No | No | |
| 2018-06-11 | 411 [mm] 20 | 19-05-07 | 556 | 140 Ye | s No | |
| 2019-05-23 | 421 [mm] 20 | 19-05-23 | 129 | 462 No | No | |
| 2018-05-29 | 356 [mm] 20 | 19-06-06 | 1347 | 2354 Ye | s No | |
| 2017-06-01 | 421 [mm] 20 | 19-06-06 | 291 | 530 Ye | s No | |
| 2017-05-29 | 429 [mm] 20 | 19-06-06 | 70 | 523 Ye | s No | |
| 2017-06-06 | 405 [mm] 20 | 19-06-07 | 547 | 275 Ye | s No | |
| 2017-06-06 | 343 [mm] 20 | 19-06-11 | 270 | 424 Ye | s No | |
| 2018-05-28 | 421 [mm] 20 | 19-06-11 | 221 | 1321 No | No | |
| 2019-06-11 | 474 [mm] 20 | 19-06-11 | 221 | 1321 No | No | |
| 2018-06-07 | 386 [mm] 20 | 19-06-12 | 2326 | 391 No | No | |
| 2019-06-12 | 389 [mm] 20 | 19-06-12 | 2326 | 391 No | No | |
| 2018-06-11 | 410 [mm] 20 | 19-07-01 | 137 | 553 Ye | s No | |
| 2017-05-29 | 425 [mm] 20 | 19-07-01 | 65 | 519 Ye | s No | |
| 2017-05-30 | 480 [mm] 20 | 19-07-04 | 167 | 429 Ye | s No | |
| 2019-05-23 | 377 [mm] 20 | 19-07-06 | 46 | 596 Ye | s No | |
| 2018-06-11 | 407 [mm] 20 | 19-07-07 | 142 | 558 Ye | s No | |
| 2018-06-08 | 394 [mm] 20 | 19-07-15 | 149 | 565 Ye | s No | |
| 2018-05-25 | 395 [mm] 20 | 19-07-22 | 2321 | 1396 Ye | s No | |
| 2018-10-24 | 592 [mm] 20 | 19-07-28 | 134 | 466 Ye | s No | |
| 2019-06-06 | 349 [mm] 20 | 19-08-13 | 186 | 1490 Ye | s No | |
| 2019-06-06 | 500 [mm] 20 | 19-09-04 | 187 | 1491 Ye | s No | |
| 2017-05-31 | 450 [mm] 20 | 19-09-05 | 500 | 201 Ye | s No | |
| 2018-05-29 | 415 [mm] 20 | 19-09-05 | 210 | 1310 Ye | s No |
Condition
Table 4. Parameter descriptions.
| Parameter | Description |
|---|---|
bWeight |
Intercept of eWeight |
bWeightLength |
Effect of Length on bWeight |
eWeight |
Log expected Weight |
LogLength |
Log-transformed and centered fork length (mm) |
sWeight |
Standard deviation of residual variation in eWeight |
Weight |
Mass (kg) |
Table 5. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bWeight | -0.0036990 | 0.1670595 | -0.036993 | -0.3419239 | 0.3149792 | 0.9773 |
| bWeightLength | 3.1710022 | 0.1832047 | 17.325243 | 2.8035274 | 3.5389078 | 0.0007 |
| sWeight | 0.0193256 | 0.0294564 | 0.984291 | 0.0008586 | 0.1062319 | 0.0007 |
Table 6. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 38 | 3 | 3 | 500 | 10 | 1304 | 1 | TRUE |
Growth
Table 7. Parameter descriptions.
| Parameter | Description |
|---|---|
Age[i] |
Scale age at capture (yr) |
bK |
Growth coefficient (mm/yr) |
bLinf |
Mean maximum length (mm) |
bT0 |
Age at zero length (yr) |
Length[i] |
Fork length at capture (mm) |
sLength |
SD of residual variation in Length |
Table 8. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bK | 0.2235899 | 0.0414649 | 5.4716353 | 0.1561642 | 0.3193449 | 0.0007 |
| bLInf | 449.7879798 | 14.0211403 | 32.1310130 | 425.7101733 | 479.2432565 | 0.0007 |
| bT0 | -0.2442682 | 0.7104428 | -0.3837309 | -1.7881108 | 1.0088049 | 0.7267 |
| sLength | 22.3656309 | 3.1870066 | 7.1616761 | 17.6684189 | 30.1849697 | 0.0007 |
Table 9. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 32 | 4 | 3 | 500 | 100 | 1270 | 1.001 | TRUE |
Survival
Table 10. Parameter descriptions.
| Parameter | Description |
|---|---|
bDetected |
Monthly probability of detection if inlake |
bMortality |
Log odds monthly probability of dying of natural causes |
bMortalityHandling |
Effect of capture and handling on bMortality |
bMoved |
Monthly probability of being detected moving between sections if alive |
bRecaptured |
Monthly probability of being recaptured if alive |
bReported |
Monthly probability of being reported if recaptured with one or more T-bar tags |
bTagLoss |
Monthly probability of loss for a single T-bar tag |
Table 11. Model coefficients.
| term | estimate | sd | zscore | lower | upper | pvalue |
|---|---|---|---|---|---|---|
| bDetected | 0.8966457 | 0.0066512 | 134.794960 | 0.8826788 | 0.9096324 | 0.0007 |
| bMortality | -5.1998574 | 0.3843645 | -13.618153 | -6.0669245 | -4.5710811 | 0.0007 |
| bMortalityHandling | 0.5746340 | 0.5599843 | 1.018155 | -0.5624161 | 1.6418533 | 0.3200 |
| bMoved | 0.8539965 | 0.0081915 | 104.235398 | 0.8374648 | 0.8696397 | 0.0007 |
| bRecaptured | 0.0061447 | 0.0009421 | 6.590763 | 0.0045532 | 0.0081882 | 0.0007 |
| bReported | 0.9844942 | 0.0200206 | 48.858289 | 0.9216218 | 0.9993276 | 0.0007 |
| bTagLoss | 0.0028539 | 0.0015934 | 1.981170 | 0.0010039 | 0.0071287 | 0.0007 |
Table 12. Model summary.
| n | K | nchains | niters | nthin | ess | rhat | converged |
|---|---|---|---|---|---|---|---|
| 14130 | 7 | 3 | 500 | 300 | 135 | 1.027 | FALSE |
Yield-per-Recruit
Table 13. Summary of parameters in yield-per-recruit model.
| Parameter | Ecotype | Estimate | Description | Source |
|---|---|---|---|---|
| tmax | Small | 3.00e+01 | The maximum age (yr). | Current Study |
| k | Small | 2.24e-01 | The VB growth coefficient (yr-1). | Current Study |
| Linf | Large | 7.50e+01 | The VB mean maximum length (cm). | Professional Judgement |
| Linf | Small | 4.50e+01 | The VB mean maximum length (cm). | Current Study |
| t0 | Small | -2.44e-01 | The (theoretical) age at zero length (yr). | Current Study |
| k2 | Small | 1.50e-01 | The VB growth coefficient after length L2 (yr-1). | Default |
| Linf2 | Small | 1.00e+02 | The VB mean maximum length after length L2 (cm). | Default |
| L2 | Small | 1.00e+03 | The length (or age if negative) at which growth switches from the first to second phase (cm or yr). | Default |
| Wb | Small | 3.17e+00 | The weight (as a function of length) scaling exponent. | Current Study |
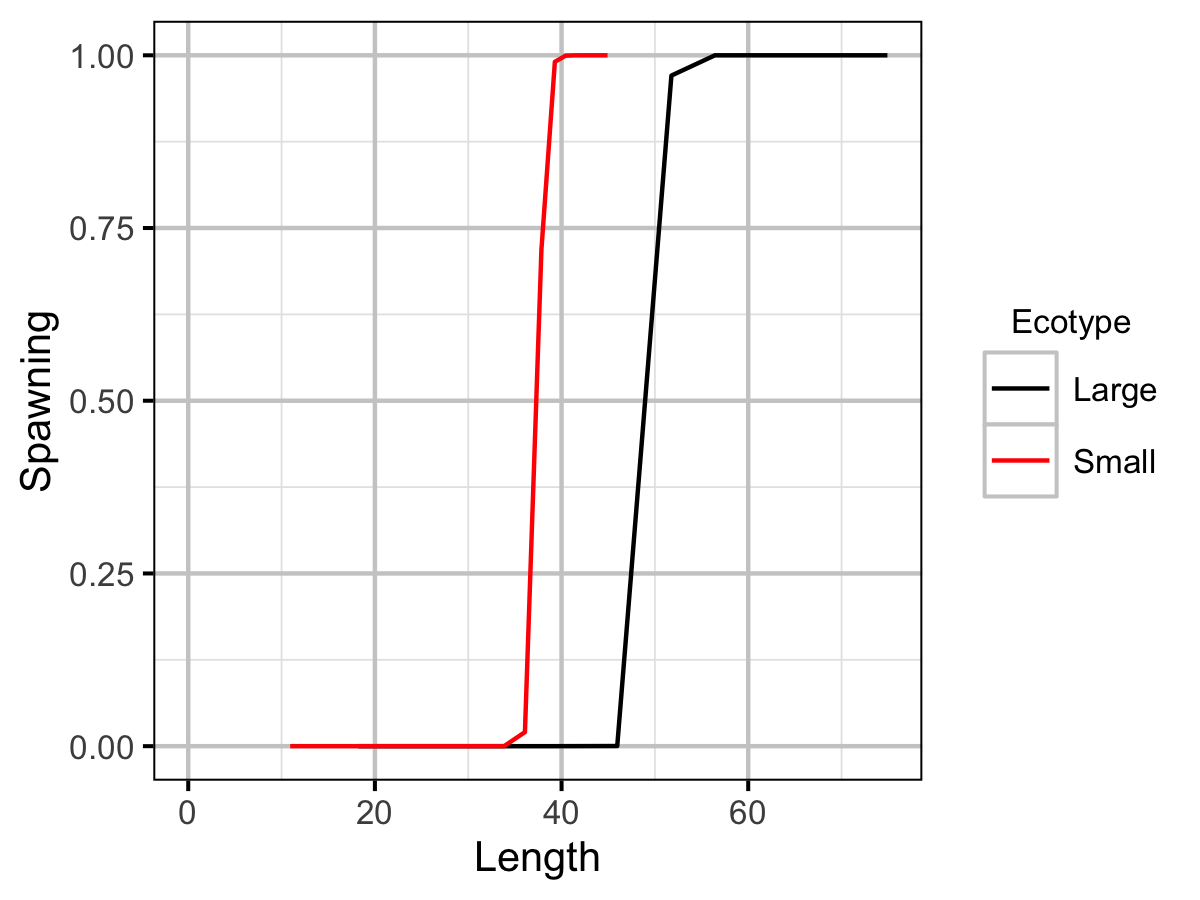
| Ls | Large | 5.00e+01 | The length (or age if negative) at which 50 % mature (cm or yr). | Professional Judgement |
| Ls | Small | 3.75e+01 | The length (or age if negative) at which 50 % mature (cm or yr). | Spin Gillnetting |
| Sp | Small | 1.00e+02 | The maturity (as a function of length) power. | Default |
| es | Small | 1.00e+00 | The annual probability of a mature fish spawning. | Default |
| Sm | Small | 0.00e+00 | The spawning mortality probability. | Default |
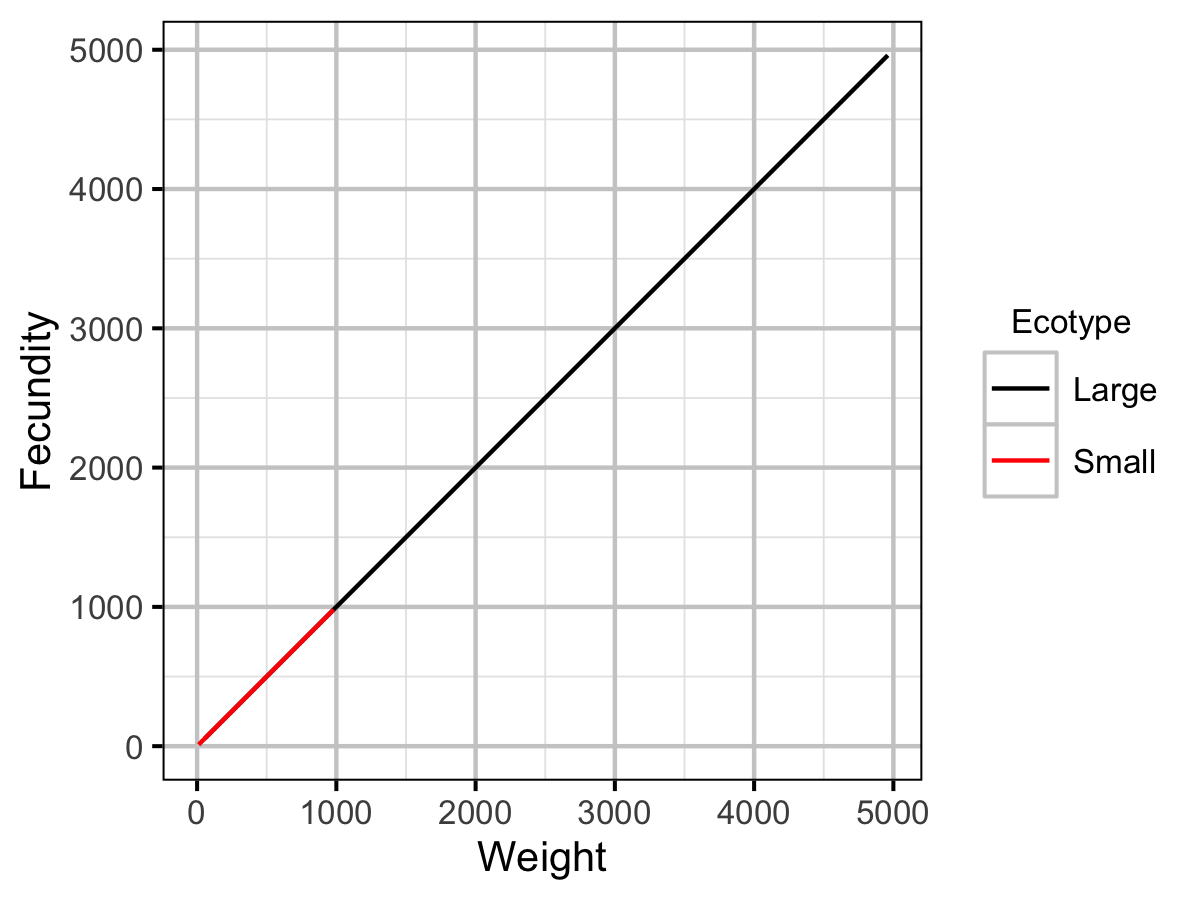
| fb | Small | 1.00e+00 | The fecundity (as a function of weight) scaling exponent. | Default |
| tR | Small | 1.00e+00 | The age from which survival is density-independent (yr). | Default |
| BH | Small | 1.00e+00 | Recruitment follows a Beverton-Holt (1) or Ricker (0) relationship. | Default |
| Rk | Small | 2.50e+01 | The lifetime spawners per spawner at low density. | Myers et al. 1999 |
| n | Small | 1.50e-01 | The annual interval natural mortality rate from age tR. | Default |
| nL | Small | 6.39e-02 | The annual interval natural mortality rate from length Ln. | Current Study |
| Ln | Small | 5.00e+01 | The length (or age if negative) at which the natural mortality rate switches from n to nA (cm or yr). | Default |
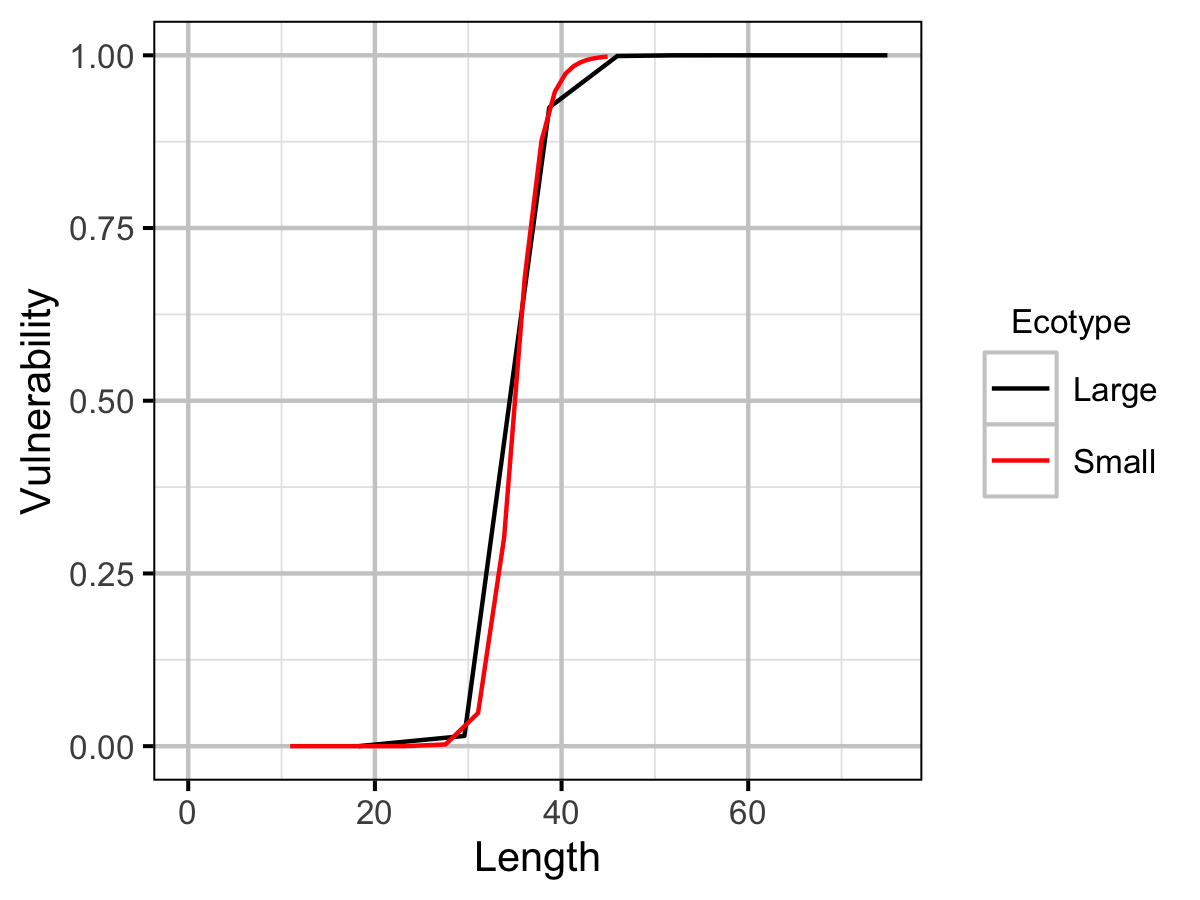
| Lv | Small | 3.50e+01 | The length (or age if negative) at which 50 % vulnerable to harvest (cm or yr). | Professional Judgement |
| Vp | Small | 2.50e+01 | The vulnerability to harvest (as a function of length) power. | Professional Judgement |
| Llo | Small | 0.00e+00 | The lower harvest slot length (cm). | Default |
| Lup | Small | 1.00e+02 | The upper harvest slot length (cm). | Default |
| Nc | Small | 0.00e+00 | The slot limits non-compliance probability. | Default |
| pi | Small | 7.13e-02 | The annual capture probability. | Current Study |
| rho | Small | 0.00e+00 | The release probability. | Default |
| Hm | Small | 0.00e+00 | The hooking mortality probability. | Default |
| Rmax | Small | 1.00e+00 | The number of recruits at the carrying capacity (ind). | Default |
| Wa | Small | 5.64e-03 | The (extrapolated) weight of a 1 cm individual (g). | Current Study |
| fa | Small | 1.00e+00 | The (theoretical) fecundity of a 1 g female (eggs). | Default |
| q | Small | 1.00e-01 | The catchability (annual probability of capture) for a unit of effort. | Default |
Table 14. Lake Trout large ecotype yield-per-recruit calculations including the capture probability (pi), exploitation rate (u) and average age, length and weight of fish harvested.
| Type | pi | u | Yield | Age | Length | Weight | Effort |
|---|---|---|---|---|---|---|---|
| actual | 0.0712952 | 0.0712952 | 0.2996335 | 8.921062 | 58.59212 | 2608.401 | 0.7020118 |
| optimal | 0.1595423 | 0.1595423 | 0.3731851 | 6.514245 | 53.53010 | 1984.422 | 1.6496570 |
Table 15. Lake Trout small ecotype yield-per-recruit calculations including the capture probability (pi), exploitation rate (u) and average age, length and weight of fish harvested.
| Type | pi | u | Yield | Age | Length | Weight | Effort |
|---|---|---|---|---|---|---|---|
| actual | 0.0712952 | 0.0712952 | 0.1185490 | 10.578893 | 39.61731 | 673.1236 | 0.7020118 |
| optimal | 0.3541295 | 0.3541295 | 0.2344587 | 8.064988 | 37.37973 | 557.0976 | 4.1491465 |
Figures
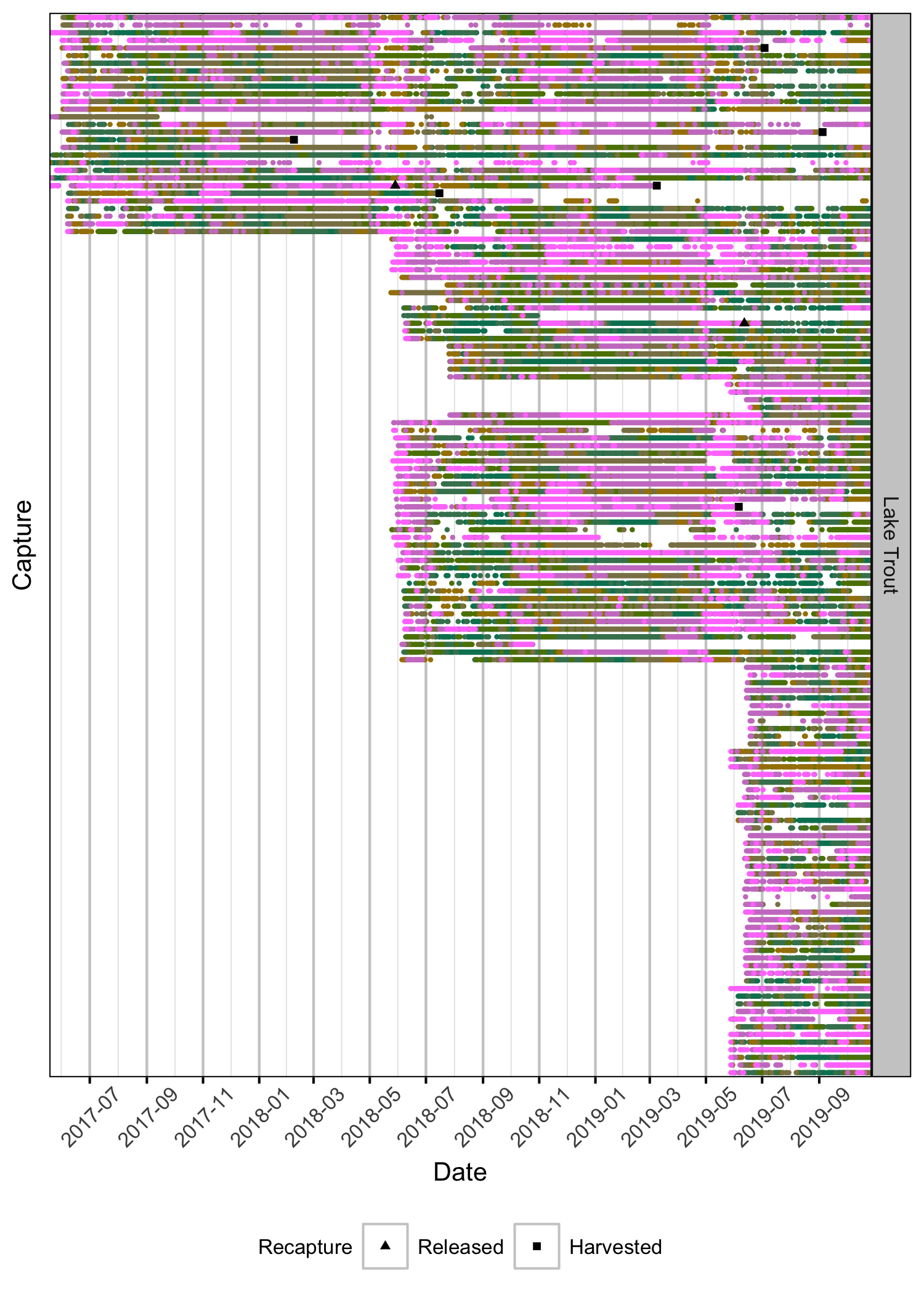
Captures
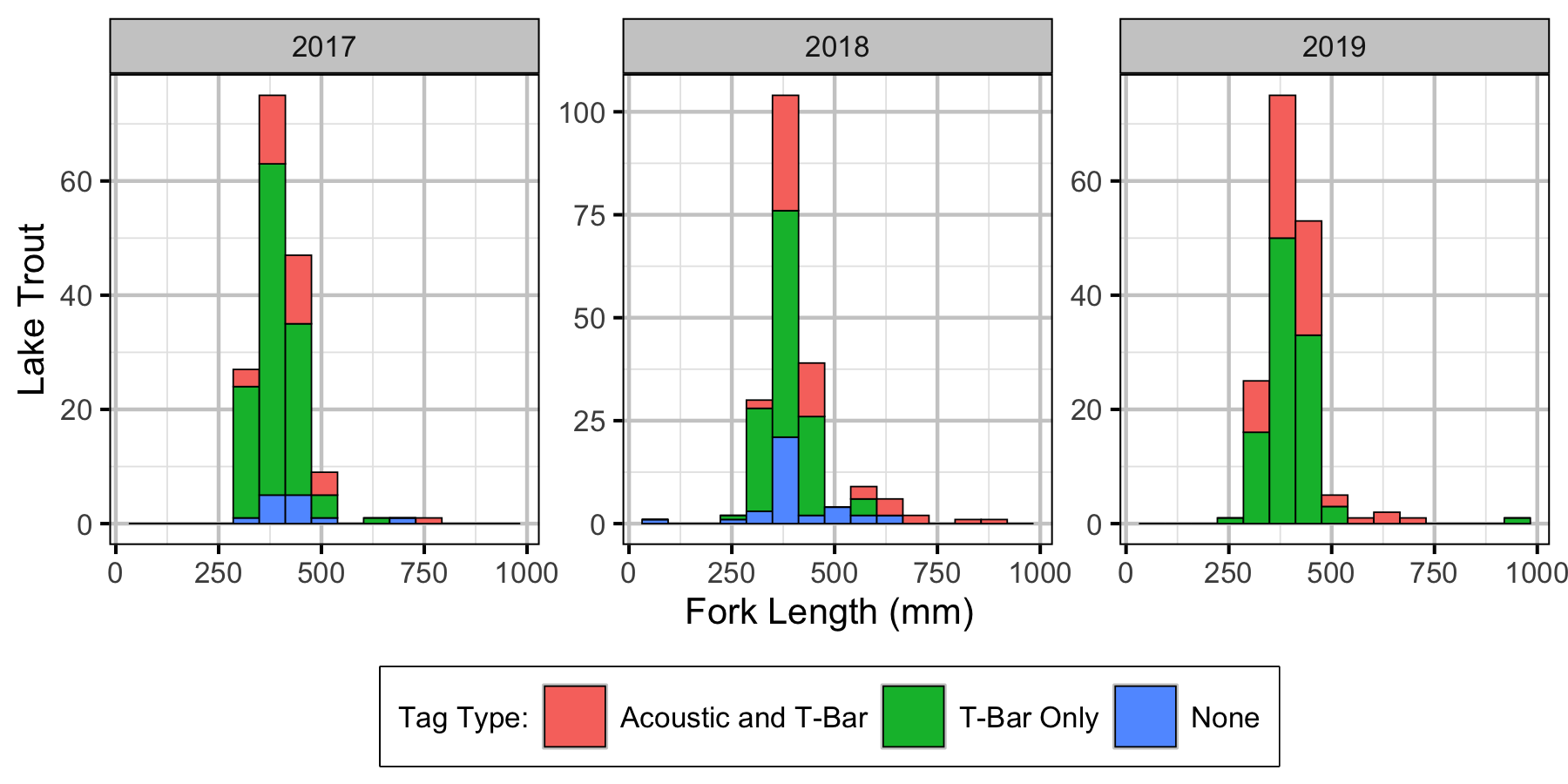
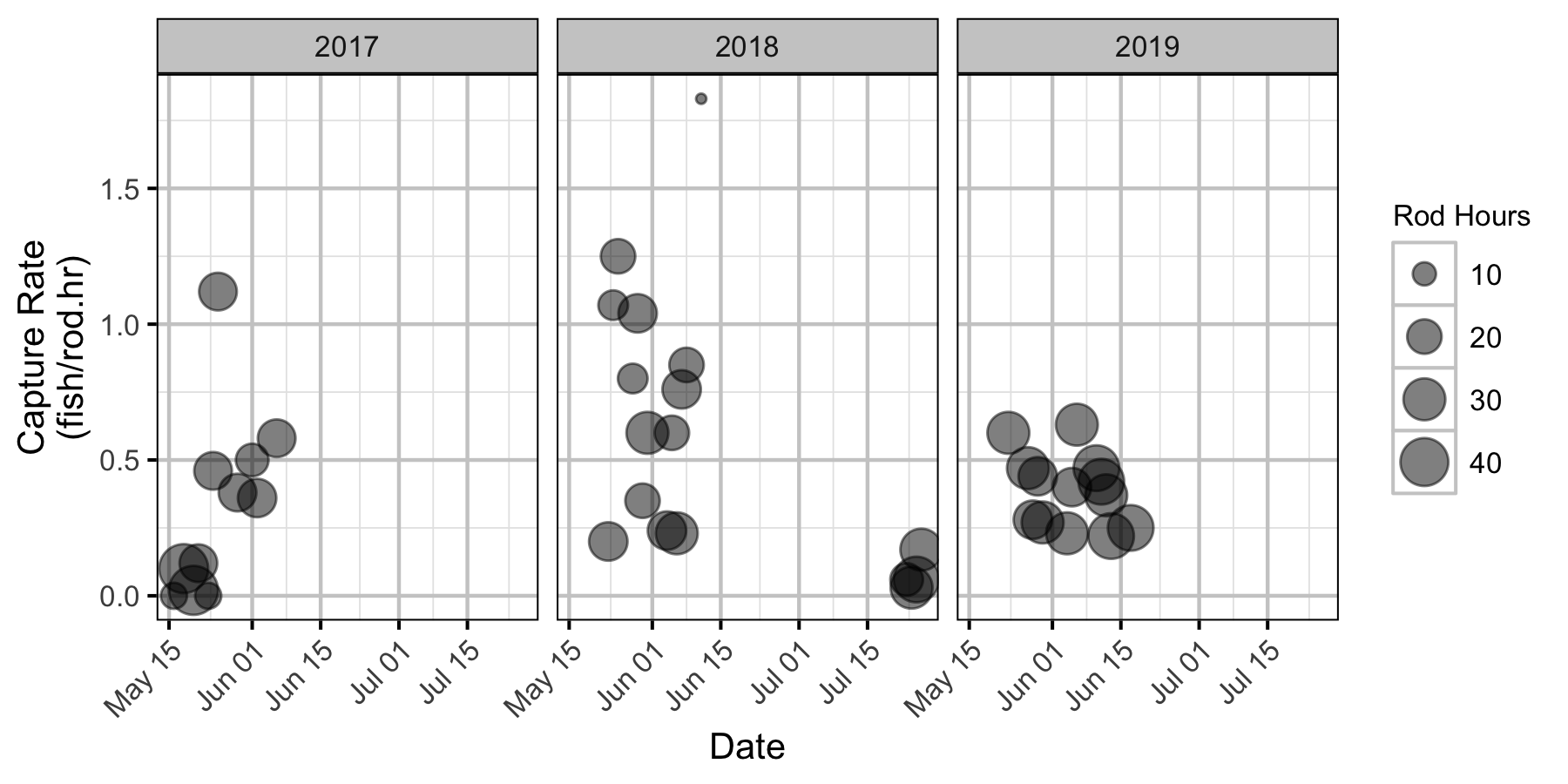
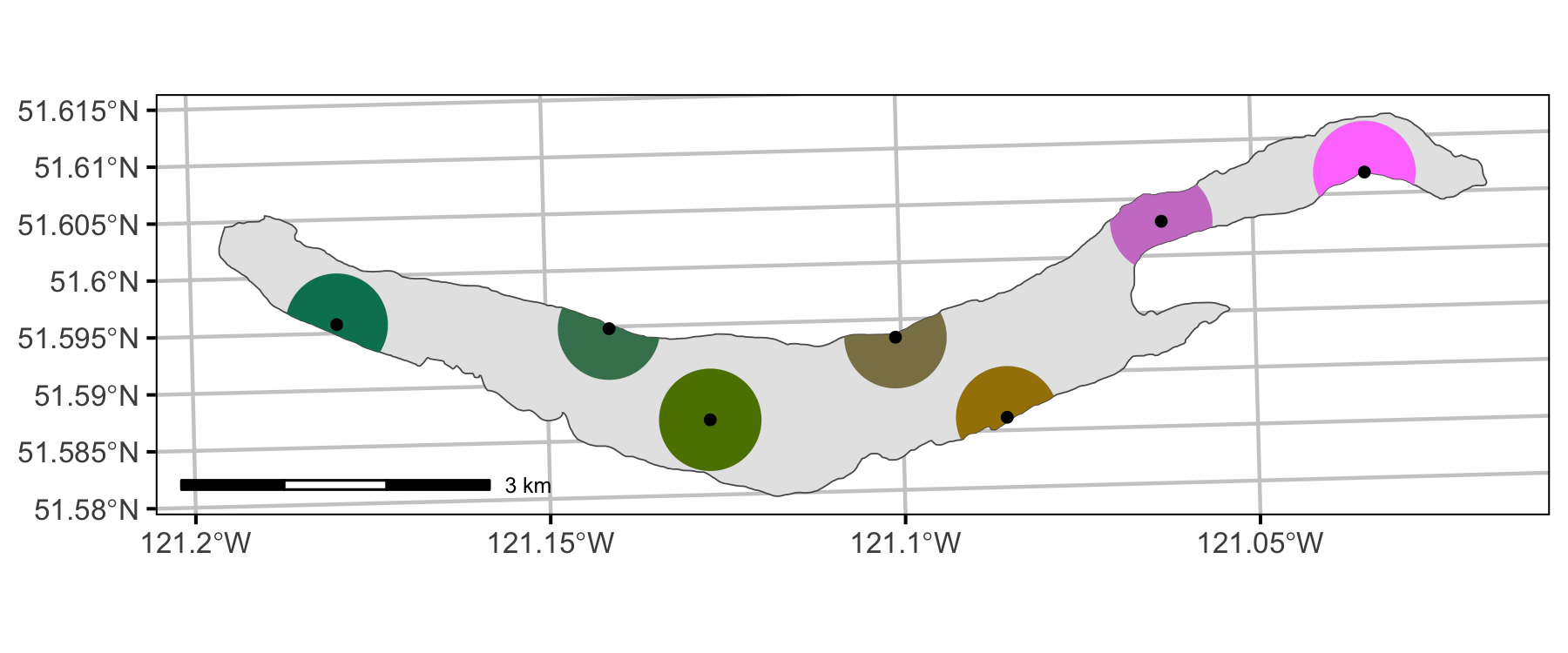
Coverage
Detections
Condition
Growth
Survival
Yield-per-Recruit
Recommendations
Recommendations include:
- Continue annual mobile receiver surveys.
Acknowledgements
The organisations and individuals whose contributions have made this analysis report possible include:
- MFLNRO - Cariboo Region
- Russ Bobrowski
- Scott Horley
References
Bradford, Michael J, Josh Korman, and Paul S Higgins. 2005. “Using Confidence Intervals to Estimate the Response of Salmon Populations (Oncorhynchus Spp.) to Experimental Habitat Alterations.” Canadian Journal of Fisheries and Aquatic Sciences 62 (12): 2716–26. https://doi.org/10.1139/f05-179.
Brooks, Steve, Andrew Gelman, Galin L. Jones, and Xiao-Li Meng, eds. 2011. Handbook for Markov Chain Monte Carlo. Boca Raton: Taylor & Francis.
Fabrizio, Mary C., Bruce L. Swanson, Stephen T. Schram, and Michael H. Hoff. 1996. “Comparison of Three Nonlinear Models to Describe Long-Term Tag Shedding by Lake Trout.” Transactions of the American Fisheries Society 125 (2): 261–73. https://doi.org/10.1577/1548-8659(1996)125<0261:COTNMT>2.3.CO;2.
He, Ji X., James R. Bence, James E. Johnson, David F. Clapp, and Mark P. Ebener. 2008. “Modeling Variation in Mass-Length Relations and Condition Indices of Lake Trout and Chinook Salmon in Lake Huron: A Hierarchical Bayesian Approach.” Transactions of the American Fisheries Society 137 (3): 801–17. https://doi.org/10.1577/T07-012.1.
Kery, Marc, and Michael Schaub. 2011. Bayesian Population Analysis Using WinBUGS : A Hierarchical Perspective. Boston: Academic Press. http://www.vogelwarte.ch/bpa.html.
McDermid, Jenni L., Brian J. Shuter, and Nigel P. Lester. 2010. “Life History Differences Parallel Environmental Differences Among North American Lake Trout (Salvelinus Namaycush) Populations.” Canadian Journal of Fisheries and Aquatic Sciences 67 (2): 314–25. https://doi.org/10.1139/F09-183.
Plummer, Martyn. 2015. “JAGS Version 4.0.1 User Manual.” http://sourceforge.net/projects/mcmc-jags/files/Manuals/4.x/.
R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Thorley, Joseph L., and Greg F. Andrusak. 2017. “The Fishing and Natural Mortality of Large, Piscivorous Bull Trout and Rainbow Trout in Kootenay Lake, British Columbia (2008–2013).” PeerJ 5 (January): e2874. https://doi.org/10.7717/peerj.2874.
von Bertalanffy, L. 1938. “A Quantitative Theory of Organic Growth (Inquiries on Growth Laws Ii).” Human Biology 10: 181–213.
Walters, Carl J., and Steven J. D. Martell. 2004. Fisheries Ecology and Management. Princeton, N.J: Princeton University Press.